The following truth table belongs to which one of the following four gates?
∣∣
∣
∣
∣
∣
∣∣ABC110100010001∣∣
∣
∣
∣
∣
∣∣
OR
NAND
XOR
NOR
The correct Answer is:D
To determine which logic gate corresponds to the given truth table, we will analyze the outputs based on the inputs. The truth table provided is:
| A | B | C | Output |
|---|---|---|--------|
| 1 | 1 | 0 | ? |
| 1 | 0 | 0 | ? |
| 0 | 1 | 0 | ? |
| 0 | 0 | 1 | ? |
1. Identify the Inputs and Outputs:
- The inputs are A, B, and C.
- We need to determine the output for each combination of inputs.
2. Analyze the Output for Each Combination:
- For the first row (A=1, B=1, C=0): The output is 0.
- For the second row (A=1, B=0, C=0): The output is 0.
- For the third row (A=0, B=1, C=0): The output is 0.
- For the fourth row (A=0, B=0, C=1): The output is 1.
3. Compare with Logic Gates:
- AND Gate: Outputs 1 only when all inputs are 1. (Does not match)
- OR Gate: Outputs 1 when at least one input is 1. (Does not match)
- NAND Gate: Outputs 0 only when all inputs are 1. (Does not match)
- NOR Gate: Outputs 1 only when all inputs are 0. (Matches with the last row)
4. Confirm the NOR Gate:
- The NOR gate outputs 0 for any input combination that includes at least one 1, and outputs 1 only when all inputs are 0.
- From the truth table, we see that the output is 0 for the first three combinations and 1 for the last combination, which confirms that this truth table corresponds to a NOR gate.
5. Final Conclusion:
- The truth table belongs to the NOR gate.
|---|---|---|--------|
| 1 | 1 | 0 | ? |
| 1 | 0 | 0 | ? |
| 0 | 1 | 0 | ? |
| 0 | 0 | 1 | ? |
- The inputs are A, B, and C.
- We need to determine the output for each combination of inputs.
- For the first row (A=1, B=1, C=0): The output is 0.
- For the second row (A=1, B=0, C=0): The output is 0.
- For the third row (A=0, B=1, C=0): The output is 0.
- For the fourth row (A=0, B=0, C=1): The output is 1.
- AND Gate: Outputs 1 only when all inputs are 1. (Does not match)
- OR Gate: Outputs 1 when at least one input is 1. (Does not match)
- NAND Gate: Outputs 0 only when all inputs are 1. (Does not match)
- NOR Gate: Outputs 1 only when all inputs are 0. (Matches with the last row)
- The NOR gate outputs 0 for any input combination that includes at least one 1, and outputs 1 only when all inputs are 0.
- From the truth table, we see that the output is 0 for the first three combinations and 1 for the last combination, which confirms that this truth table corresponds to a NOR gate.
- The truth table belongs to the NOR gate.
Topper's Solved these Questions
- SEMICONDUCTORSBOOK - RESONANCE ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Exercise
100 Videos
- SEMICONDUCTORSBOOK - RESONANCE ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Exercise 2
16 Videos
- REVISION DPPBOOK - RESONANCE ENGLISHCHAPTER - REVISION DPPEXERCISE - All Questions
463 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
Similar Questions
The following truth table corresponds to the logic gate
∣∣ ∣ ∣ ∣ ∣ ∣∣ABX000011101111∣∣ ∣ ∣ ∣ ∣ ∣∣
View SolutionGiven the following truth table where A , B are inputs and Y the output :
ABY001101011110
The output Y is :
View SolutionGiven truth table is related with :-
ABY110011101001
View SolutionThe truth table given below is for :-
ABY001010100111
View SolutionIf A=⎡⎢⎣100101010⎤⎥⎦, then
View SolutionIn the following digital circuit, what will be the output at ‘Z’, when the input (A,B) are (1,0) , (0,0), (1,1),(0,1) :
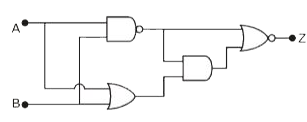
View SolutionThe given truth table relates Y to A and B.
ABY001010100110
Then, Y is given by
View SolutionAn X-OR gate has following truth table:
It is represented by following logic relation
y=¯¯¯A.B+A.¯¯¯B
Build this gate using AND, OR and NOT gates.
∣∣ ∣ ∣ ∣ ∣ ∣∣ABY000011101110∣∣ ∣ ∣ ∣ ∣ ∣∣
View SolutionFour identical charges are placed at the points (1,0,0),(0,1,0),(−1,0,0), and (0,−1,0). Then,
View Solutionwhich of the following is/are true for
Δ=∣∣ ∣ ∣∣a21a+c0b2+1b+c0b+cc2+1∣∣ ∣ ∣∣ ?
View Solution
