Consider a solid sphere of density ρ and radius 4R. Centre of the sphere is at origin. Two spherical cavities centred at (2R,0) and (−2R,0) are created in sphere. Radii of both cavities is R. In left cavity material of density 2ρ is filled while second cavity is kept empty. What is gravitational field at origin. 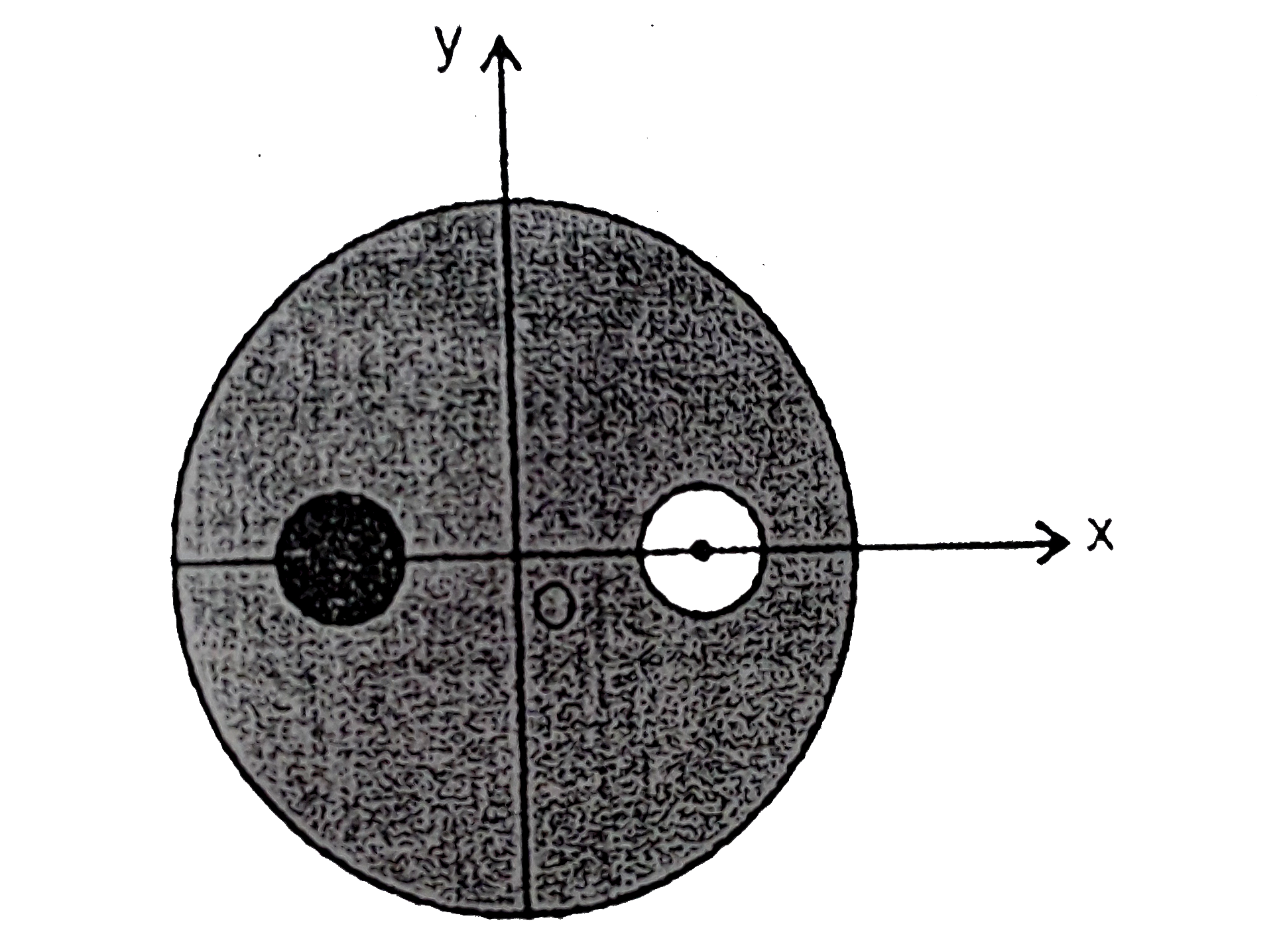
GρπR3
2GpπR3
4GρπR3
3GρπR2
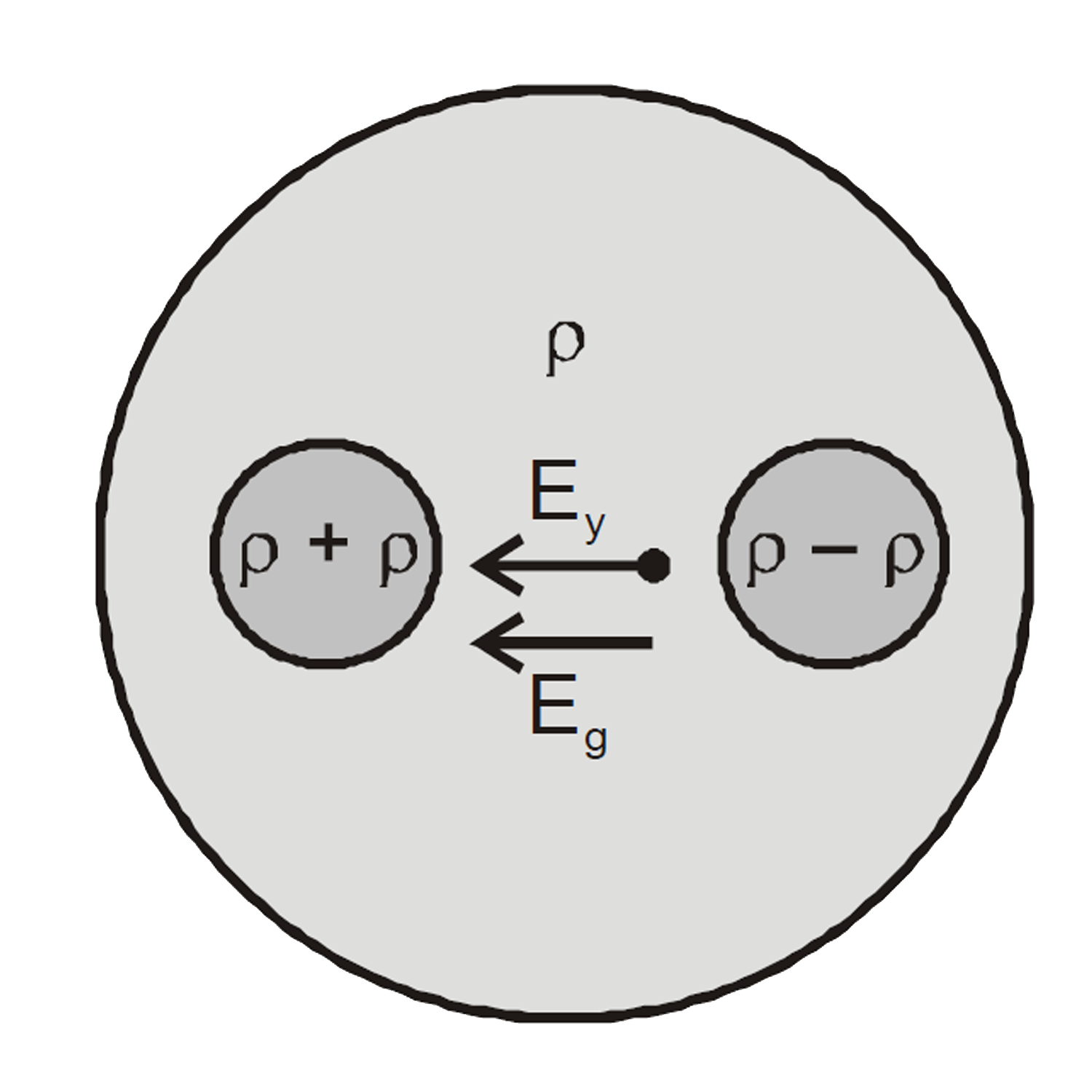
Above distribution can be represented as shown in figure. Gravitational field due to sphere of radius R at a distance 3R
Eg=Gρ43πR34R2=GρπR3
so net field at center will be 2Fg=2GρπR3
Topper's Solved these Questions
Similar Questions
A solid sphere having uniform charge density ρ and radius R is shown in figure. A spherical cavity ofradius R2 is made in it. What is the potential at point O?
 View Solution
View SolutionA solid sphere of uniform density and radius 4 units is located with its centre at the origin O of coordinates. Two sphere of equal radii 1 unit, with their centres at A(-2,0 ,0) and B(2,0,0) respectively, are taken out of the solid leaving behind spherical cavities as shown if fig Then:
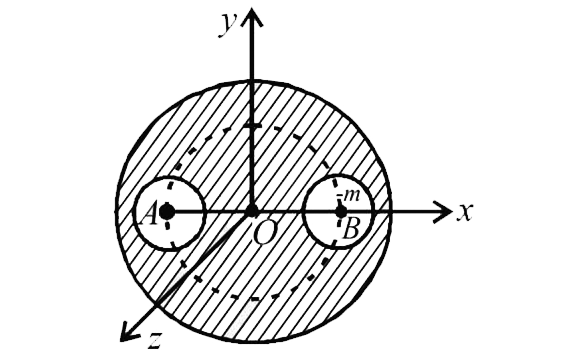
The gravitational field due to this object at the orgin is zero.
The gravitational force at point B(2, 0, 0) is zero.
The gravitational force at point B(2, 0, 0) is zero.
Both (1) & (3)View Solution
Knowledge Check
- Question 1 - Select One
A solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F1 on a particle placed at P, distance 2R from the centre O of the sphere. A spherical cavity of radius R/2 is now made in the sphere as shown in figure. The particle with cavity now applies a gravitational force F2 on same particle placed at P. The radio F2/F1 will be
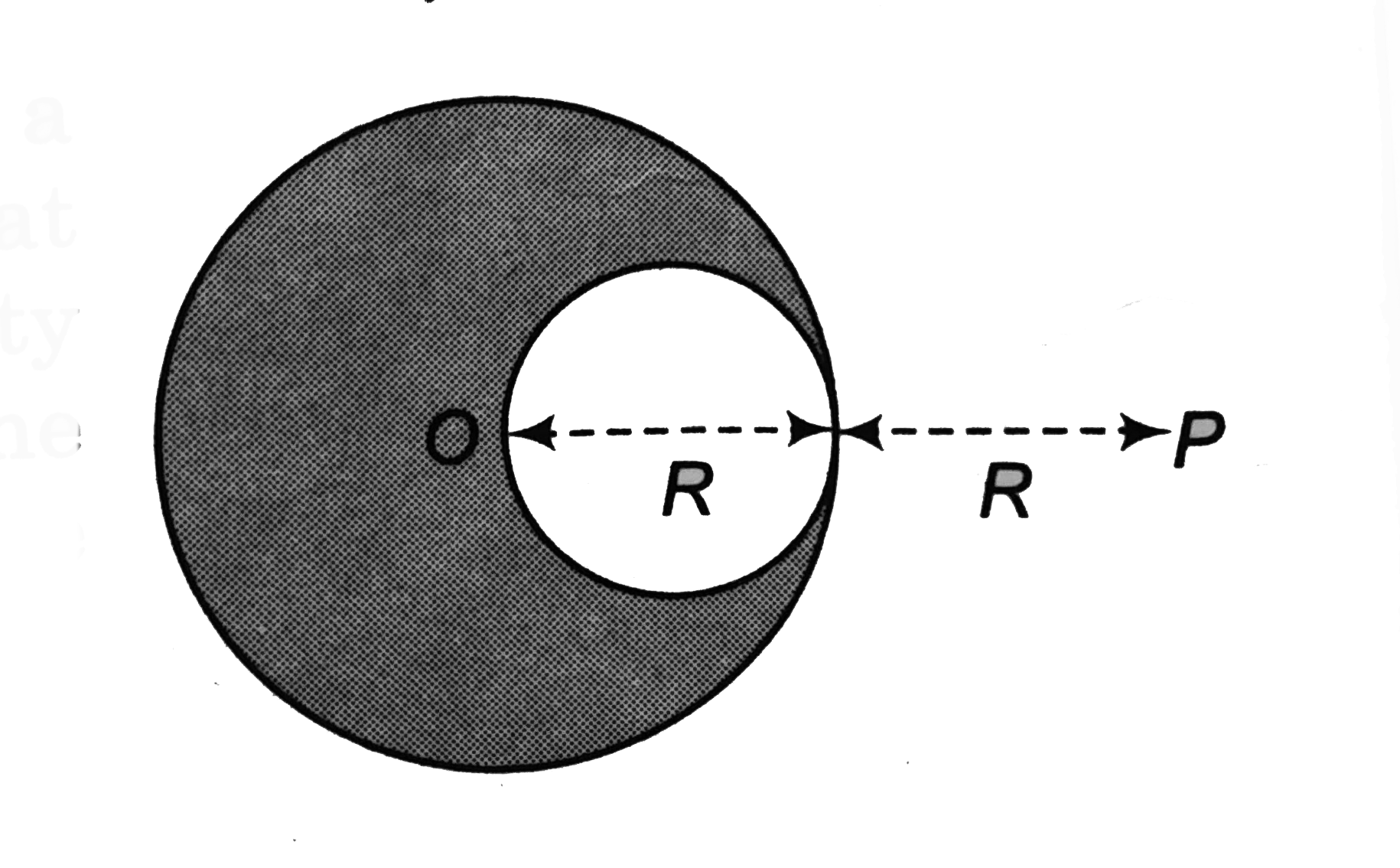 A1/2B7/9C3D7
A1/2B7/9C3D7
The figure represents a solid uniform sphere of mass M and radius R. A spherical cavity of radius r is at a distance a from the centre of the sphere. The gravitational field inside the cavity is
 View Solution
View SolutionA solid sphere of uniform density and radius 4 units is located with its centre at the origin O of coordinates. Two sphere of equal radii 1 unit, with their centres at A(-2,0 ,0) and B(2,0,0) respectively, are taken out of the solid leaving behind spherical cavities as shown if fig Then:
 View Solution
View SolutionA solid sphere of uniform density and radius 4 units is located with its centre at the origin O of coordinates. Two sphere of equal radii 1 unit, with their centres at A(-2,0 ,0) and B(2,0,0) respectively, are taken out of the solid leaving behind spherical cavities as shown if fig Then:
 View Solution
View SolutionA uniform solid sphere of radius R has a cavity of radius 1m cut from it if centre of mass of the system lies at the periphery of the cavity then
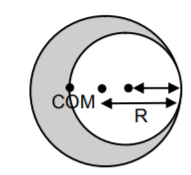 View Solution
View SolutionA uniform solid sphere of radius R has a cavity of radius 1m cut from it if centre of mass of the system lies at the periphery of the cavity then
 View Solution
View SolutionA hemi-spherical cavity is created in solid sphere (of radius 2R) as shown in the figure. Then
 View Solution
View SolutionIn a diagramatic sphere is a cavity is made it at its centre and now paramagnetic material is inserted in the cavity. the sphere is kept in an external magnetic field at centre
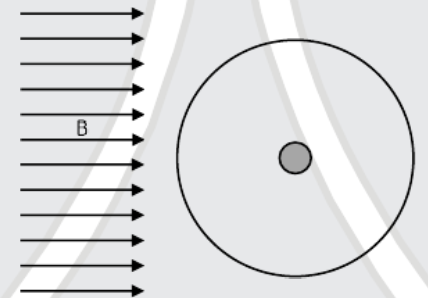 View Solution
View Solution

