Mobility of electron in N-type Ge is 5000cm2/volt sec and conductivity 5mho/cm. If effect of holes is negligible then impurity concentration will be
6.25×1015/cm3
9.25×1014/cm3
6×1013/cm3
9×1013/cm3
The correct Answer is:A
To find the impurity concentration in N-type germanium given the mobility of electrons and conductivity, we can use the formula for conductivity:
σ=ne⋅e⋅μe
Where:
- σ is the conductivity (in mho/cm),
- ne is the electron concentration (in cm−3),
- e is the charge of an electron (1.6×10−19 coulombs),
- μe is the mobility of electrons (in cm2/(volt·sec)).
1. Identify the given values:
- Mobility of electrons, μe=5000cm2/volt sec
- Conductivity, σ=5mho/cm
- Charge of an electron, e=1.6×10−19C
2. Rearrange the formula for conductivity to solve for electron concentration ne:
ne=σe⋅μe
3. Substitute the known values into the equation:
ne=5mho/cm(1.6×10−19C)⋅(5000cm2/volt sec)
4. Calculate the denominator:
e⋅μe=1.6×10−19×5000=8.0×10−16C cm2/volt sec
5. Now calculate ne:
ne=58.0×10−16=6.25×1015cm−3
6. Conclusion:
The impurity concentration ne in N-type germanium is 6.25×1015cm−3.
Final Answer:
The impurity concentration is 6.25×1015cm−3.
---
- σ is the conductivity (in mho/cm),
- ne is the electron concentration (in cm−3),
- e is the charge of an electron (1.6×10−19 coulombs),
- μe is the mobility of electrons (in cm2/(volt·sec)).
- Mobility of electrons, μe=5000cm2/volt sec
- Conductivity, σ=5mho/cm
- Charge of an electron, e=1.6×10−19C
ne=σe⋅μe
ne=5mho/cm(1.6×10−19C)⋅(5000cm2/volt sec)
e⋅μe=1.6×10−19×5000=8.0×10−16C cm2/volt sec
ne=58.0×10−16=6.25×1015cm−3
The impurity concentration ne in N-type germanium is 6.25×1015cm−3.
The impurity concentration is 6.25×1015cm−3.
Topper's Solved these Questions
- SEMICONDUCTORSBOOK - RESONANCE ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Exercise 2
16 Videos
- SEMICONDUCTORSBOOK - RESONANCE ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Exercise 3
88 Videos
- SEMICONDUCTORSBOOK - RESONANCE ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Exercise 3
88 Videos
- REVISION DPPBOOK - RESONANCE ENGLISHCHAPTER - REVISION DPPEXERCISE - All Questions
463 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
Similar Questions
The product of the hole concentration and the conduction electron concentration turns out to be independent of the amount of any impurity doped. The concentration of conduction electrons in germanium is 6×1019per cubic metre. When some phosphorus impurity is doped into a germanium sample, the concentration of conduction electrons increases to 2×1028per cubic metre.Find the concentration of the holes in the doped germanium.
View SolutionMobility of electrons in a semiconductor is defined as the ratio of their drift velocity to the applied electric field. If, for an n-type semiconuctor, the density of electrons is 1019m−3 and their mobility is 1.6m2/(V.s) then the resistivity of the semiconductor (since it is an n-type semiconductor contribution of holes is ignored) is close to :
View SolutionIn an intrinsic semiconductor the energy gap Egis1.2eV. Its hole mobility is much smaller than electron mobility and independent of temperature. What is the ratio between conductivity at 600K and 300K? Assume that temperature dependence intrinstic concentration ni is given by
ni=n0exp(−Eg2kT), where n0 is a constant and k=8.62×10−5eV/K.
View SolutionThe contribution in the total current flowing through a semiconductor due to electrons and holes are 34 and 14 respectively. If the drift velocity of electrons is 52 times that of holes at this temperature, then the ratio of concentration of electrons and holes is
View SolutionA: When a pure semiconductor is doped with a pentavalent impurity, the number of conduction electrons is increased while the number of holes is decreased
R: Some of the holes get recombined with the conduction electrons as the concentration of the conduction electrons is increased.
View SolutionA potential difference of 5 V is applied across a conductor of length 10 cm . If drift velcoity of electrons is 2.5×10−4m/s , then electron mobility will be
View Solution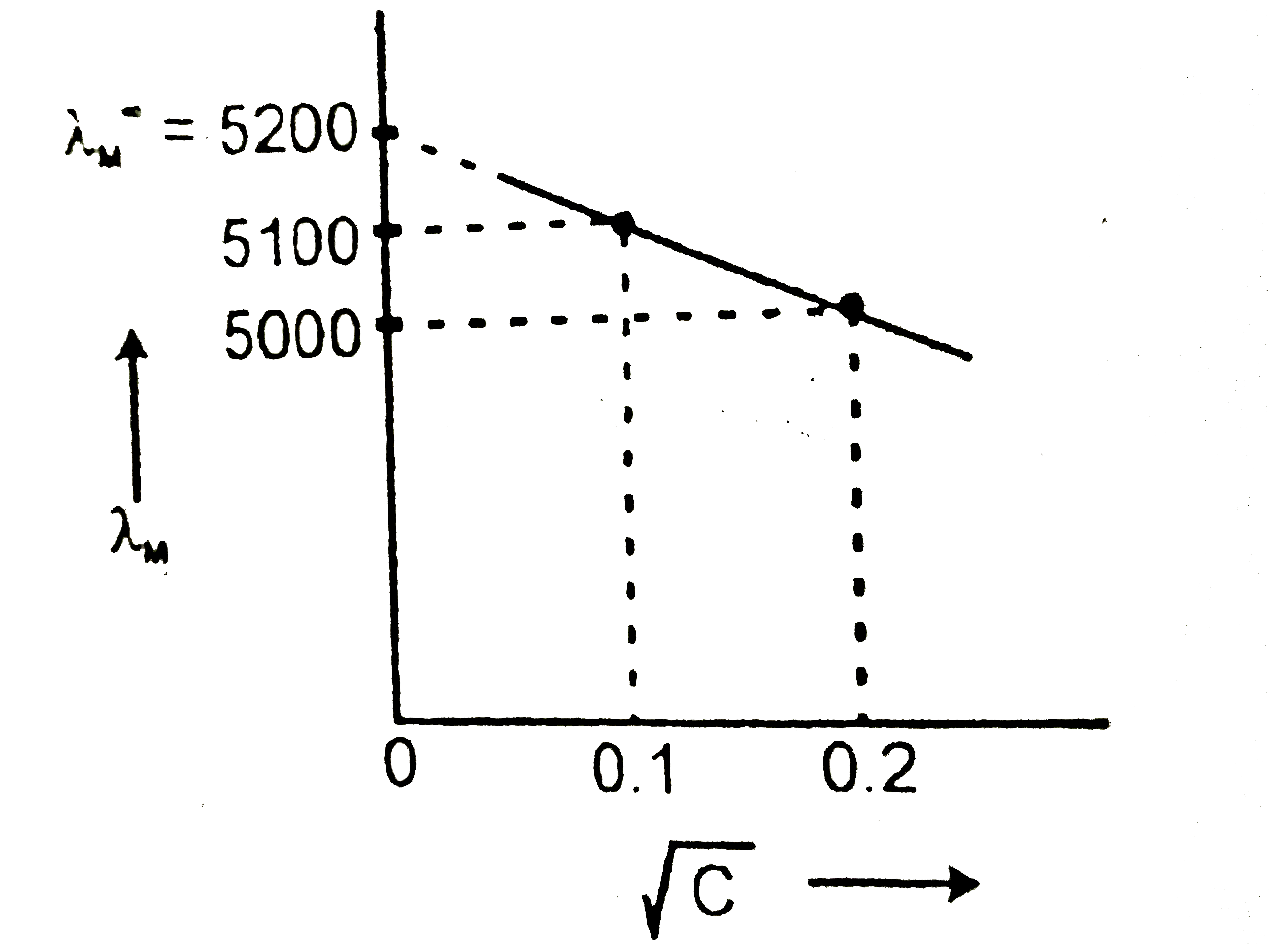
At 0.04 M concentration the molar conductivity of a solution of a electrolyte is 5000Ω−1cm2mol−1 while at 0.01 M concentration the value is 5100Ω−1cm2mol−1 making necessary assumption (taking it as strong electrolyte) find the molar conductivity at infinite dilution and also determine the degree of dissociation of strong electrolyte at 0.04M.
View SolutionAt 0.04 M concentration, the molar conductivity of solution of an electrolyte is 5000Ω−1cm2mol−1 while at 0.01 M concentration the value is 5100Ω−1cm2mol−1. Making necessary assumption (Taking it as strong electrolyte) find the molar conductivity at infinite dilution and write percentage dissociation of strong electrolyte at 0.04 M.
View Solutionwhich of the following statements are true about semiconductor ?
(a)silicon doped with electron rich impurity is a p-type semiconductor
(b)Silicon doped with an electrons rich impurity is an n-type semiconductor
(c)Delocalised electrons increase the conductivity of doped silicon
(d)An electron vacancy increase the conductivity of n- type semiconductor
View SolutionA semiconductor having electron and linear mobilities μn and μp respectively.
If its intrinsic carrier density is ni, then what will be the value of hole concentration P for which the conductivity will be maximum at a given temperature?
View Solution
