The quantity 2UfkT represents (where U= internal energy of gas)
mass of the gas
kinetic energy of the gas
number of moles of the gas
number of molecules in the gas
The correct Answer is:D
To solve the problem, we need to analyze the expression 2UfkT where U is the internal energy of the gas, f is the degrees of freedom, k is the Boltzmann constant, and T is the temperature.
1. Understand the Internal Energy of an Ideal Gas:
The internal energy U of an ideal gas can be expressed as:
U=nFRT2
where n is the number of moles, F is the degrees of freedom, and R is the universal gas constant.
2. Substituting R with k:
We can also express the universal gas constant R in terms of the Boltzmann constant k:
R=NAk
where NA is Avogadro's number. Thus, we can rewrite the internal energy as:
U=nF(NAk)T2
3. Rearranging the Internal Energy Expression:
Simplifying the expression for U:
U=nFNAkT2
4. Finding 2UfkT:
Now, we need to compute 2UfkT:
2UfkT=2(nFNAkT2)fkT
The 2 in the numerator and denominator cancels out:
=nFNAkTfkT
5. Simplifying Further:
The kT in the numerator and denominator also cancels out:
=nFf
Since F is the degrees of freedom, the expression simplifies to:
=n
6. Conclusion:
Therefore, we find that:
2UfkT=n
This means that the quantity 2UfkT represents the number of moles of the gas.
Final Answer:
The quantity 2UfkT represents the number of moles of the gas.
The internal energy U of an ideal gas can be expressed as:
U=nFRT2
where n is the number of moles, F is the degrees of freedom, and R is the universal gas constant.
We can also express the universal gas constant R in terms of the Boltzmann constant k:
R=NAk
where NA is Avogadro's number. Thus, we can rewrite the internal energy as:
U=nF(NAk)T2
Simplifying the expression for U:
U=nFNAkT2
Now, we need to compute 2UfkT:
2UfkT=2(nFNAkT2)fkT
The 2 in the numerator and denominator cancels out:
=nFNAkTfkT
The kT in the numerator and denominator also cancels out:
=nFf
Since F is the degrees of freedom, the expression simplifies to:
=n
Therefore, we find that:
2UfkT=n
This means that the quantity 2UfkT represents the number of moles of the gas.
The quantity 2UfkT represents the number of moles of the gas.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - KTG & THERMODYNAMICSEXERCISE - Exercise-21videos
KTG & THERMODYNAMICS
- BOOK - RESONANCE ENGLISHCHAPTER - KTG & THERMODYNAMICSEXERCISE - PART -I15videos
KTG & THERMODYNAMICS
- BOOK - RESONANCE ENGLISHCHAPTER - KTG & THERMODYNAMICSEXERCISE - PART -II17videos
KTG & THERMODYNAMICS
- BOOK - RESONANCE ENGLISHCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Exercise64videos
KINETIC THEORY OF GASES AND THERMODYNAMICS
- BOOK - RESONANCE ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Exercise64videos
MAGNETIC FIELD AND FORCES
Similar Questions
An ideal gas can be taken form initial state 1 to final state 2 by two different process. Let ΔQ and W represent the heat given and work done by the system. Then which quantities is/are same in both process (where ΔU= internal energy of gas)
View SolutionWhat do you mean by internal energy (U) of a gas ?
View SolutionWhich of the following diagram correctly represents the variation of internal energy (U) of gas under expansion at constant temperature.
View SolutionTwo moles of an ideal monoatomic gas undergo a cyclic process which is indicated on a P−U diagram, where U is the internal energy of the gas. The work done by the gas in the cycle is k×102In2. Find k.
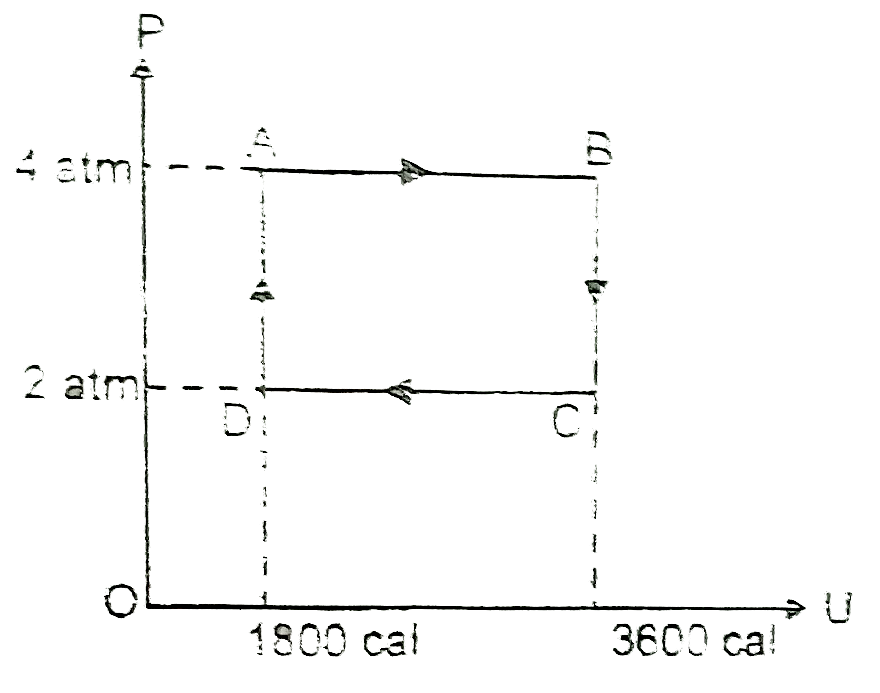 View Solution
View SolutionThe given (p - U) graph shows the variation of internal energy of an ideal gas with increase in pressure. Which of the following pressure - volume graph is equivalent to this graph ?
 .View Solution
.View SolutionA particle is placed at the origin and a force F=Kx is acting on it (where k is a positive constant). If U(0)=0, the graph of U(x) verses x will be (where U is the potential energy function.)
View SolutionA particle is placed at the origin and a force F=Kx is acting on it (where k is a positive constant). If U(0)=0, the graph of U(x) verses x will be (where U is the potential energy function.)
View SolutionAn ideal gas is taken from state 1 to state 2 through optional path A,B,CandD as shown in the PV diagram. Let Q,WandU represent the heat supplied, work done and change in internal energy of the gas respectively.
Then,
 View Solution
View SolutionAssertion: Under adiabatic free expansion, (dUdV)T is +ve when attractive forces are dominant between gas molecules [U,V,T respresent internal energy, volume and temperature of gas respectively]
Reason: Internal energy is a state function.View SolutionAn ideal monoatomic gas undergoes a process in which its internal energy U and density ρ vary as Uρ= constant. The ratio of change in internal energy and the work done by the gas is
View Solution

