If molar heat capacity of the given process (as shown in figure) is C, then

one specific heat only
C=0
C>CV
C<CV
The correct Answer is:C
dQ=dU+dW,nCdT=nCvdT+dW
ΔU>0 and ΔW>0,∴C>Cv
Topper's Solved these Questions
- KTG & THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KTG & THERMODYNAMICSEXERCISE - Exercise-2
1 Videos
- KTG & THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KTG & THERMODYNAMICSEXERCISE - PART -I
15 Videos
- KTG & THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KTG & THERMODYNAMICSEXERCISE - PART -II
17 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Exercise
64 Videos
- MAGNETIC FIELD AND FORCESBOOK - RESONANCE ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Exercise
64 Videos
Similar Questions
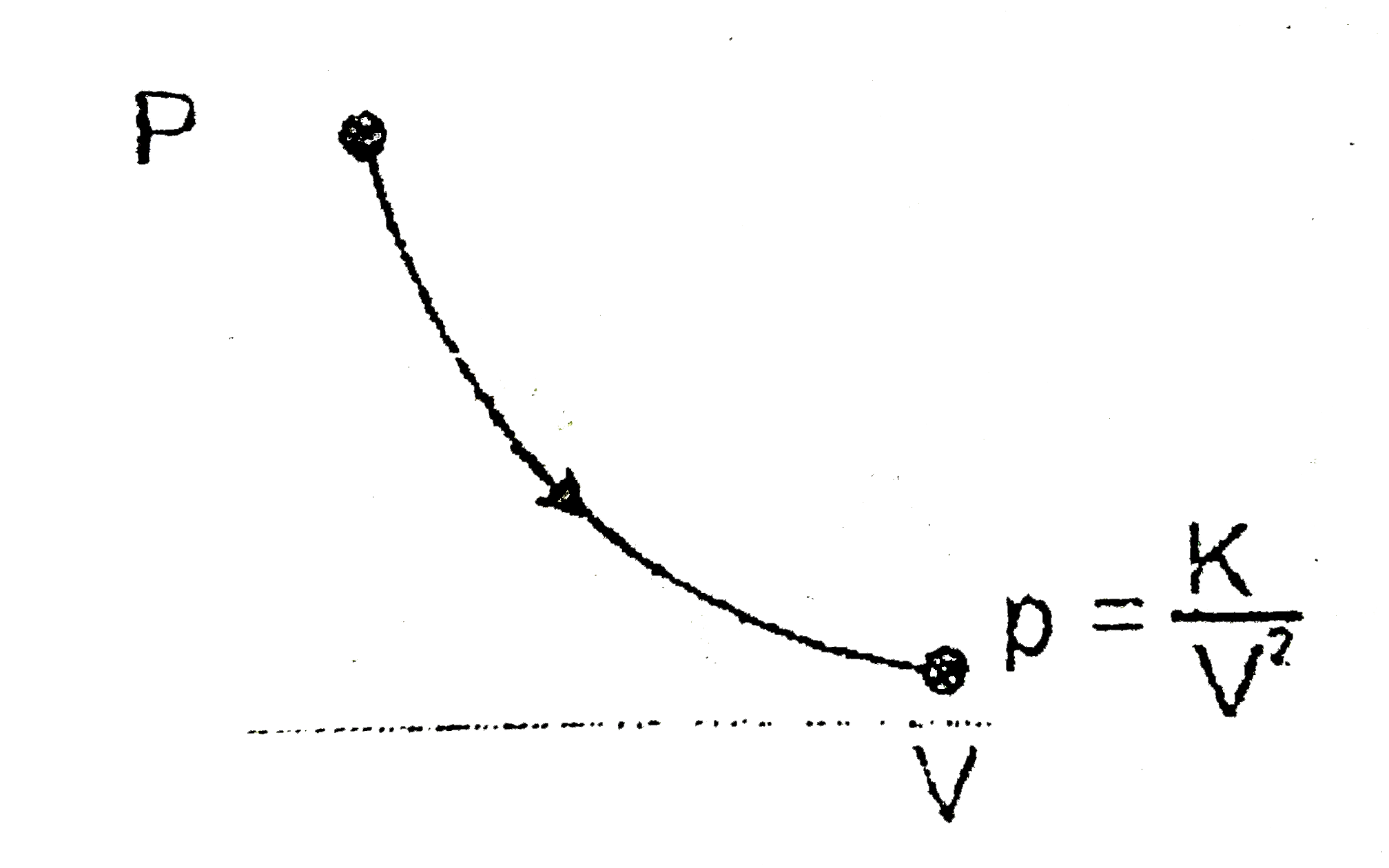
The molar heat capacity for the process shown in figure is
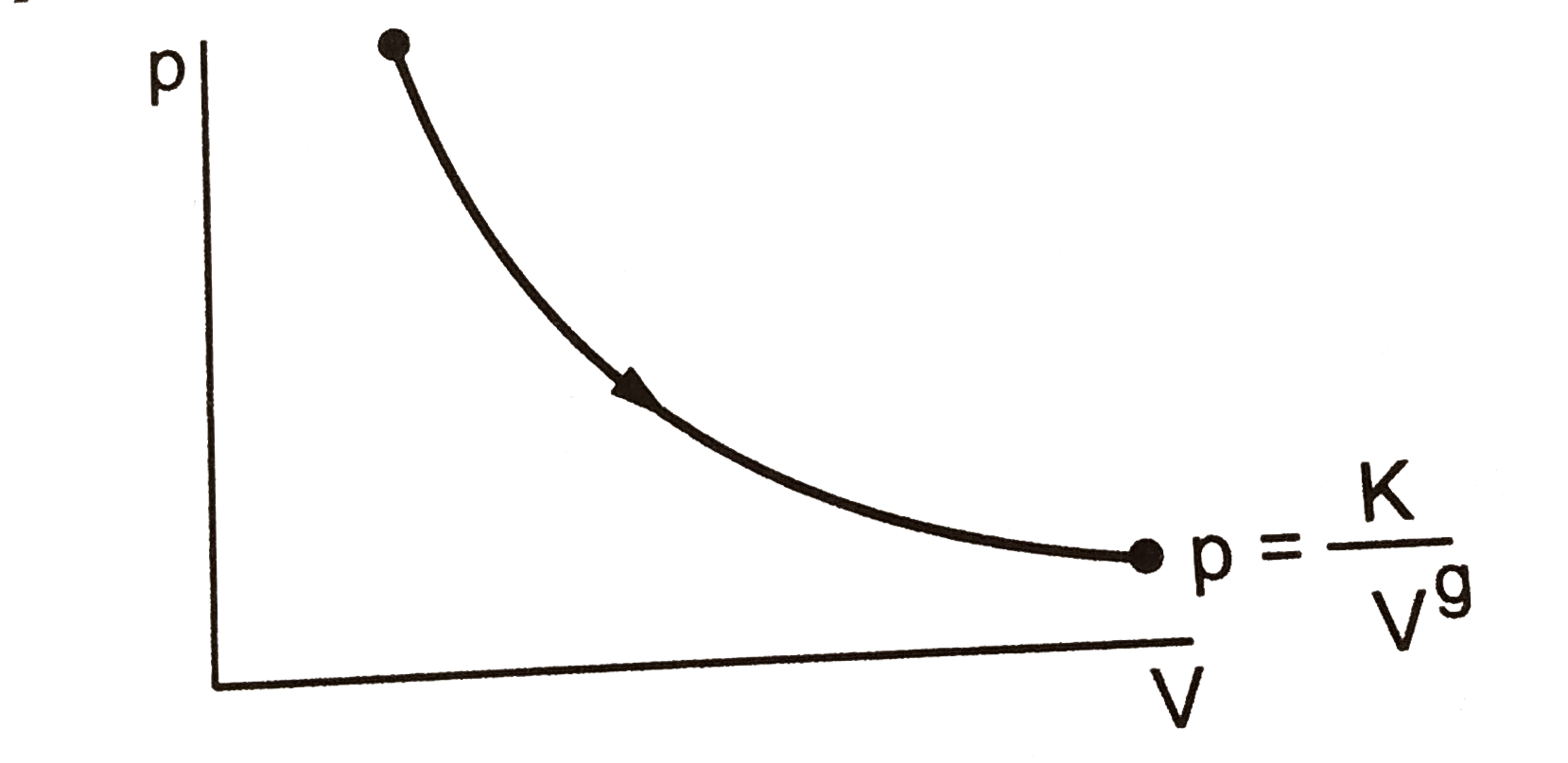
View SolutionThe molar heat capacity for the process shown in fig. is
View SolutionTemperature of two moles of a monoatomic gas is increased by 300K in the process p∝V. Find
(a) molar heat capacity of the gas in the given process
(b) heat required in the given process.
View SolutionTemperature of two moles of a monoatomic gas is increased by 300 K in the process p∝V.
(a) Find molar heat capacity of the gas in the given process.
(b) Find heat given to the gas in that.
View SolutionThe molar heat capacity for an ideal gas
View SolutionFor an ideal diatomic gas, during any process T=KV, find out the molar heat capacity of the gas during process (neglecting vibrational degree of freedom)
View SolutionThe variation of pressure versus volume is shown in the figure. The gas is diatomic and the molar specific heat capacity for the process is found to xR. Find the value of x.
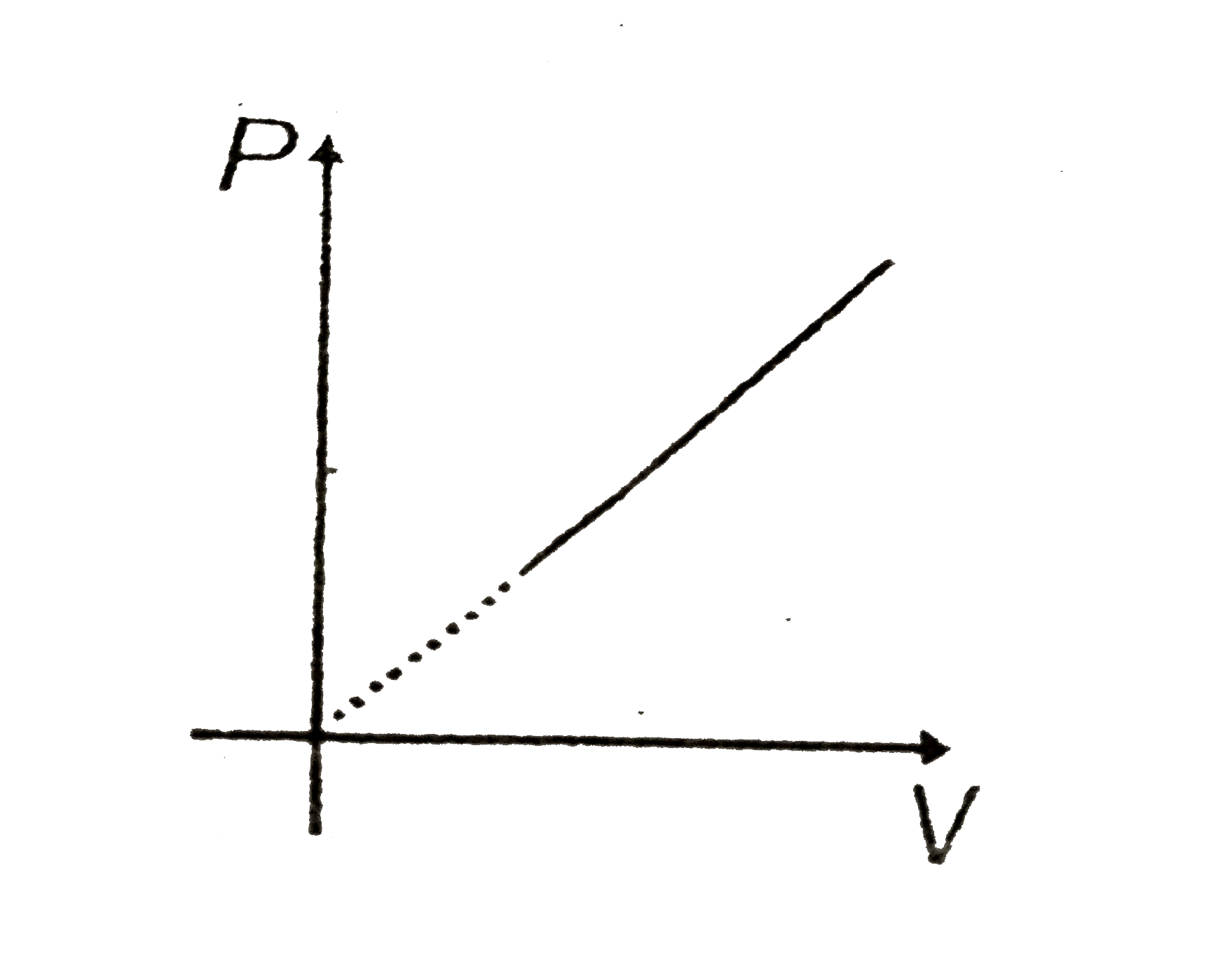 .
.
View SolutionA polytropic process for an ideal gas is represented by equation PVn=constant. If g is ratio of specific heats (CpCv), then value of n for which molar heat capacity of the process is negative is given as
View SolutionAn ideal has undergoes a polytropic given by equation PVn = constant. If molar heat capacity of gas during this process is arithmetic mean of its molar heat capacity at constant pressure and constant volume then value of n is
View SolutionAn ideal gas is taken through a process in which the pressure and the volume are changed according to the equation p=kv. Show that the molar heat capacity of the gas for the process is given by (C=Cv+R2).
View Solution
