For an ideal diatomic gas, during any process T=KV, find out the molar heat capacity of the gas during process (neglecting vibrational degree of freedom)
3R2
5R2
7R2
2R
The correct Answer is:C
T=KV⇒PV0= constant
C=Rγ−1−Rn−1=R75−1−R0−1=5R2+R
7R2
Similar Questions
For an ideal monoatomic gas during any process T=kV, find out the molar heat capacity of the gas during the process. (Assume vibrational degree of freedom to be active)
View SolutionThe molar heat capacity for an ideal gas
View Solutionan ideal diatomic gas undergoes a polytropic process described by the equation P√V=constant . The molar heat capacity of the gas during this process is
View SolutionIdeal mono-atomic gas is taken through process such that dQ = 3dU. The molar heat capacity for process is:
View SolutionP-V diagram of a diatomic gas is a straight line passing through origin. The molar heat capacity of the gas in the process will be
View SolutionP-V diagram of a diatomic gas is a straight line passing through origin. The molar heat capacity of the gas in the process will be
View SolutionOne mole of an ideal gas undergoes a process such that P∝1T. The molar heat capacity of this process is 4R.
View SolutionWhat is the molar specific heat capacity of a gas undergoing an adiabatic process ?
View SolutionThe pressure P of an ideal diatomic gas varies with its absolute temperature T as shown in figure . The molar heat capacity of gas during this process is [R is gas constant]
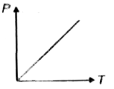View SolutionOne mole of an ideal monatomic gas undergoes a process described by the equation PV3= constant. The heat capacity of the gas during this process is
View Solution