A thermally insulated piston divides a nonconducting container in two compartements, right compartement of 2V,T and 2P, while in the left compartement the respective values are V,T and P. Total moles in total system of both comartments is 5 moles. if piston can slide freely, and in the final equilibrium position, volume of right compartement is xV5 then find the value of x.
The correct Answer is:12
To solve the problem step by step, let's break down the information given and apply the ideal gas law for both compartments.
Step 1: Understand the Initial Conditions
We have two compartments divided by a thermally insulated piston:
- Right compartment: Volume = 2V, Temperature = T, Pressure = 2P
- Left compartment: Volume = V, Temperature = T, Pressure = P
- Total moles in the system = 5 moles
Step 2: Define Moles in Each Compartment
Let:
- n1 = number of moles in the right compartment
- n2 = number of moles in the left compartment
From the problem, we know:
n1+n2=5(1)
Step 3: Apply the Ideal Gas Law
Using the ideal gas equation PV=nRT, we can express the number of moles in each compartment.
For the right compartment:
2P⋅2V=n1RT⟹n1=4PVRT(2)
For the left compartment:
P⋅V=n2RT⟹n2=PVRT(3)
Step 4: Relate the Moles
Now, we can find the ratio of moles n1 to n2 by dividing equation (2) by equation (3):
n1n2=4PVRTPVRT=4(4)
Step 5: Solve for Moles
From equation (4), we have:
n1=4n2
Substituting this into equation (1):
4n2+n2=5⟹5n2=5⟹n2=1andn1=4(5)
Step 6: Establish Equilibrium Conditions
At equilibrium, the pressures in both compartments will be equal:
n1RTV1=n2RTV2
Since the temperature T and the gas constant R are the same, they cancel out:
n1V1=n2V2(6)
Step 7: Express Volumes
Let V1 be the volume of the right compartment and V2 be the volume of the left compartment. From the problem, we know:
V1+V2=3V(since 2V+V=3V)
Substituting V2=3V−V1 into equation (6):
4V1=13V−V1
Step 8: Solve for V1
Cross-multiplying gives:
4(3V−V1)=V1⟹12V−4V1=V1⟹12V=5V1⟹V1=12V5(7)
Step 9: Relate V1 to x
From the problem, we know that the volume of the right compartment is given as:
V1=xV5
Setting this equal to equation (7):
xV5=12V5
Cancelling V from both sides:
x=12
Final Answer
Thus, the value of x is 12.
---
We have two compartments divided by a thermally insulated piston:
- Right compartment: Volume = 2V, Temperature = T, Pressure = 2P
- Left compartment: Volume = V, Temperature = T, Pressure = P
- Total moles in the system = 5 moles
Let:
- n1 = number of moles in the right compartment
- n2 = number of moles in the left compartment
n1+n2=5(1)
Using the ideal gas equation PV=nRT, we can express the number of moles in each compartment.
2P⋅2V=n1RT⟹n1=4PVRT(2)
P⋅V=n2RT⟹n2=PVRT(3)
Now, we can find the ratio of moles n1 to n2 by dividing equation (2) by equation (3):
n1n2=4PVRTPVRT=4(4)
From equation (4), we have:
n1=4n2
Substituting this into equation (1):
4n2+n2=5⟹5n2=5⟹n2=1andn1=4(5)
At equilibrium, the pressures in both compartments will be equal:
n1RTV1=n2RTV2
Since the temperature T and the gas constant R are the same, they cancel out:
n1V1=n2V2(6)
Let V1 be the volume of the right compartment and V2 be the volume of the left compartment. From the problem, we know:
V1+V2=3V(since 2V+V=3V)
Substituting V2=3V−V1 into equation (6):
4V1=13V−V1
Cross-multiplying gives:
4(3V−V1)=V1⟹12V−4V1=V1⟹12V=5V1⟹V1=12V5(7)
From the problem, we know that the volume of the right compartment is given as:
V1=xV5
Setting this equal to equation (7):
xV5=12V5
Cancelling V from both sides:
x=12
Thus, the value of x is 12.
Topper's Solved these Questions
- KTG & THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KTG & THERMODYNAMICSEXERCISE - SECTION
138 Videos
- KTG & THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KTG & THERMODYNAMICSEXERCISE - Exercise-2
1 Videos
- KTG & THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KTG & THERMODYNAMICSEXERCISE - SECTION (J)
2 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Exercise
64 Videos
- MAGNETIC FIELD AND FORCESBOOK - RESONANCE ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Exercise
64 Videos
Similar Questions
A partition divides a container having insulated walls into two compartments whose initial paraments are given. The partition is a conducting wall which can move freely without friction. Which of the following statements is/are correct, with reference to the final equilibrium position ?

View SolutionA partition divides a container having insulated walls into two compartments whose initial paraments are given. The partition is a conducting wall which can move freely without friction. Which of the following statements is/are correct, with refrence to the final equilibrium position ?

View SolutionFigure shows an insulated cylinder of volume V containing monatomic gas in both the compartments. The pistone is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate

Final volume of the left compartment.
View SolutionA rigid and insulated tank of 3m3 volume is divided into two compartments. One compartment of volume of 2m3 contains an ideal gas at 0.8314 Mpa and 400 K while the second compartment of volume of 1m3 contains the same gas at 8.314 Mpa and 500 K. If the partition between the two compartments is rptured, the final temperature of the gas is :
View SolutionFigure shows an insulated cylinder of volume V containing monatomic gas in both the compartments. The pistone is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate

The final presssures of left and right compartment respectively are
View SolutionIn the figure, a container is shown to have a movable (without friction) piston on top. The container and the piston are all made of perfectly insulated material allowing no heat transfer between outside and inside the container. The container is divided into two compartments by a rigid partition made of a thermally conducting material that allows slow transfer of heat. The lower compartment of the container is filled with 2 moles of an ideal monoatomic gas at 700K and the upper compartment is filled with 2 moles of an ideal diatomic gas at 400K. The heat capacities per mole of an ideal monoatomic gas are CV=32R,CP=52R, and those for an ideal diatomic gas are CV=52R,CP=72R,

Consider the partition to be rigidly fixed so that it does not move. When equilibrium is achieved, the final temperature of the gasses will be
View SolutionIn the figure, a container is shown to have a movable (without friction) piston on top. The container and the piston are all made of perfectly insulated material allowing no heat transfer between outside and inside the container. The container is divided into two compartments by a rigid partition made of a thermally conducting material that allows slow transfer of heat. The lower compartment of the container is filled with 2 moles of an ideal monoatomic gas at 700K and the upper compartment is filled with 2 moles of an ideal diatomic gas at 400K. The heat capacities per mole of an ideal monoatomic gas are CV=32R,CP=52R, and those for an ideal diatomic gas are CV=52R,CP=72R,

Consider the partition to be rigidly fixed so that it does not move. When equilibrium is achieved, the final temperature of the gasses will be
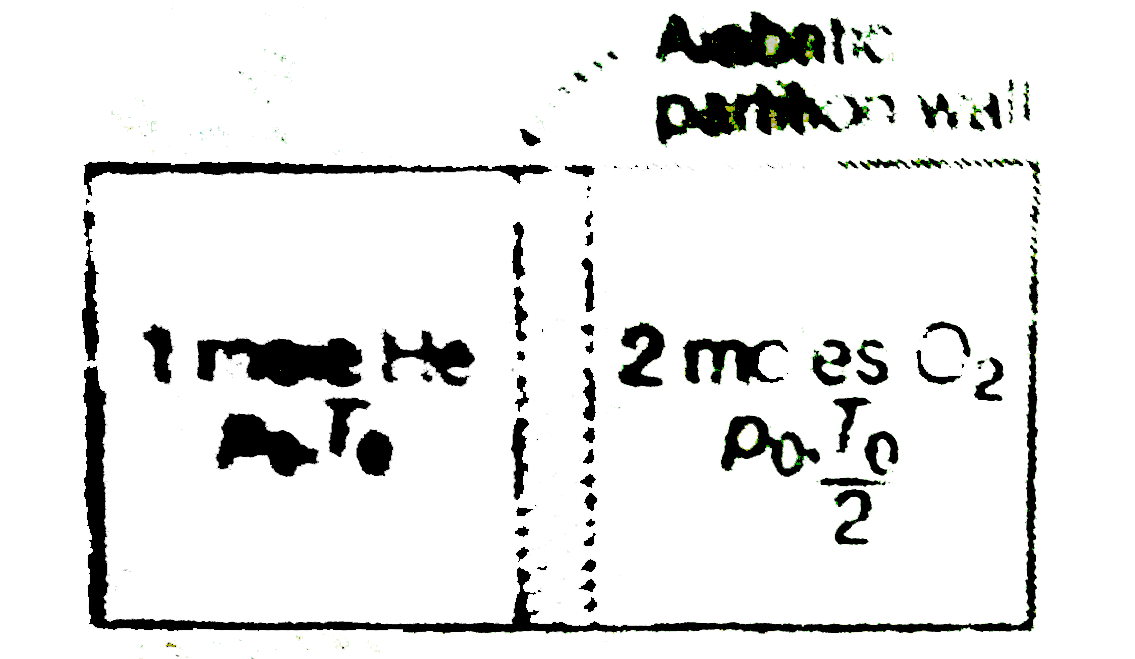
View SolutionConsider the adjacent figure. A piston divides a cylindrical container into two equal parts. The lets part contains 1 mole of helium gas and the right part contains two moles or oxygen gas. The initial temperatures and pressures of the gases in the left chamber are T0 and p0 and the right chamber are T02 and p0 respectively as shown in the figure. The piston as well as the walls of the container are adiabatic. After removal of the piston, gases mix homoganeously and the final pressure becomes p=4n13p0. Find the value of n.
View SolutionA closed gas cylinder is divided into two parts by a piston held tight. The pressure and volume of gas in two parts respectively are (P, 5V) and (10P, V). If now the piston is left free and the system undergoes isothermal process, then the volumes of the gas in two parts respectively are
View SolutionA vertical thermally insulated cylinder of volume V contain n moles of an ideal monoatomic gas under a weightless piston. A load of weight W is placed on the piston as a result of which the piston is displaced. If the initial temp of the gas is 300K, area of piston is A and atmospheric pressure P0. (take W=P0A). Determine the value of final temperature of the gas
View Solution
