A closed gas cylinder is divided into two parts by a piston held tight. The pressure and volume of gas in two parts respectively are (P, 5V) and (10P, V). If now the piston is left free and the system undergoes isothermal process, then the volumes of the gas in two parts respectively are
4V, 2V
5V , V
2V , 4V
3V , 3V
The correct Answer is:C
Step by step video & image solution for A closed gas cylinder is divided into two parts by a piston held tight. The pressure and volume of gas in two parts respectively are (P, 5V) and (10P, V). If now the piston is left free and the system undergoes isothermal process, then the volumes of the gas in two parts respectively are by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
The pressure p and volume V of an ideal gas both increase in a process.
View SolutionA vessel of volume V is divided into two parts by a partition. The pressure of the gas in one part is p1 and that in the other part is p2. If the partition is removed find the pressure of the gas in the vessel.
View SolutionThe pressure P and volume V of an ideal gas both decreases in a process.
View SolutionA thermally insulated container is divided into two parts by a screen. In one part the pressure and temperature are P and T for an ideal gas filled. In the second part it is vacuum. If now a small hole is created in the screen, then the temperature of the gas will
View SolutionInitial pressure and volume of a gas are P and V respectively. First its volume is expanded to 4V by isothermal process and then again its volume makes to be V by adiabatic process then its final pressure is (γ=1.5) -
View SolutionA masslesss piston divides a closed thermallyy insulated cylinder into two equal parts. One part contains M = 28 g of nitrogen. At this temperature, one-third of molecules are dissociated into atoms and the other part is evacuated. The piston is released and the gas fills the whole volume of the cylinder at temperature T0. Then, the piston is slowly displaced back to its initial position. calculate the increases in internal energy of the gas. Neglect further dissociation of molecules during, the motion of the piston.
View SolutionA vertical cylinder of cross-sectional area 0.1m2 closed at both ends is fitted with a frictionless piston of mass M dividing the cylinder into two parts. Each part contains one mole of an ideal gas in equilibrium at 300K. The volume of the upper part is 0.1m3 and that of lower part is 0.05m3 .What force must be applied to the piston so that the volumes of the two parts remain unchanged when the temperature is increased to 500K?
View SolutionFig shows a cylindrical tube of volume V with adiabatic walls containing an ideal gas. The internal energy of this ideal gas is given by 1.5nRT. The tube is divided into two equal parts by a fixed diathermic wall. Initially, the pressure and the temperature are p1,T1 on the left and p2,T2 on the right. the system is left for sufficient time so that the temperature becomes equal on the two sides. (a) how much work has been done by the gas on the left part ? (b) find the final pressures on the two sides. (c ) find the final equilibrium temperature. (d) how much heat has flown from the gas on the right to the gas on the left ?
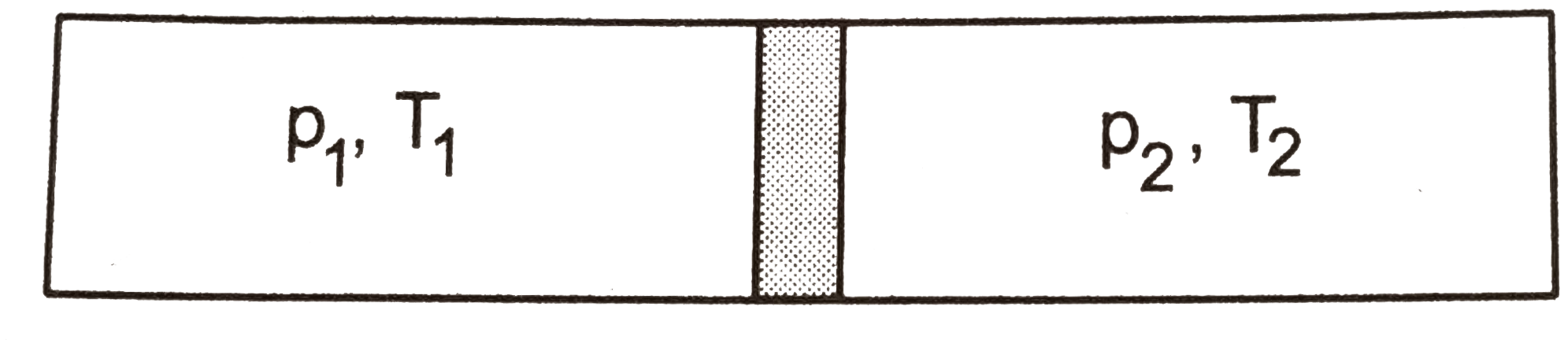 View Solution
View SolutionA weightless piston divides a thermally insulated cylinder into two parts of volumes V and 3V.2 moles of an ideal gas at pressure P=2 atmosphere are confined to the part with volume V=1 litre. The remainder of the cylinder is evacuated. The piston is now released and the gas expands to fill the entire space of the cylinder. The piston is then pressed back to the initial position. Find the increase of internal energy in the process and final temperature of the gas. The ratio of the specific heats of the gas, γ=1.5.
View SolutionA cylindrical vessel made of thermally insulating material is divided into two equal parts by an insulating and. Movable piston. Both parts contain ideal monoatomic gas . The gas in the left part is supplied heat such that the volume of right part becomes one-eight of its initial volume . Work done by the gas in the right part is
 View Solution
View Solution
