The temperature of a hot liquid in a container of negligible heat capacity falls at the rate of 3K/min due to heat emission to the surroundings, just before it begins to solidify. The temperature then remains constant for 30min, by the time the liquid has all solidfied. Find the ratio of specific heat capacity of liquid to specific latent heat of fusion.
The correct Answer is:190
To solve the problem, we need to find the ratio of the specific heat capacity of the liquid (S) to the specific latent heat of fusion (L). Let's break down the solution step by step.
Step 1: Understand the problem
The temperature of the liquid falls at a rate of 3K/min until it reaches the point of solidification, after which it remains constant for 30min while it solidifies.
Step 2: Calculate the total temperature drop before solidification
The temperature drop in 30min can be calculated as follows:
ΔT=Rate of temperature drop×Time=3K/min×30min=90K
Step 3: Calculate the heat released during cooling
The heat released during the cooling of the liquid can be expressed using the formula:
QR=m⋅S⋅ΔT
Substituting the values we have:
QR=m⋅S⋅90
Step 4: Calculate the heat required for solidification
When the liquid begins to solidify, the heat required for this process is given by:
QS=m⋅L
Step 5: Set the heat released equal to the heat required
Since the heat released during cooling equals the heat required for solidification, we can set the two equations equal to each other:
QR=QS
Substituting the expressions we derived:
m⋅S⋅90=m⋅L
Step 6: Simplify the equation
We can cancel m from both sides (assuming m≠0):
S⋅90=L
Step 7: Find the ratio of specific heat capacity to specific latent heat of fusion
Rearranging the equation gives us:
SL=190
Final Answer
Thus, the ratio of the specific heat capacity of the liquid to the specific latent heat of fusion is:
SL=190
---
The temperature of the liquid falls at a rate of 3K/min until it reaches the point of solidification, after which it remains constant for 30min while it solidifies.
The temperature drop in 30min can be calculated as follows:
ΔT=Rate of temperature drop×Time=3K/min×30min=90K
The heat released during the cooling of the liquid can be expressed using the formula:
QR=m⋅S⋅ΔT
Substituting the values we have:
QR=m⋅S⋅90
When the liquid begins to solidify, the heat required for this process is given by:
QS=m⋅L
Since the heat released during cooling equals the heat required for solidification, we can set the two equations equal to each other:
QR=QS
Substituting the expressions we derived:
m⋅S⋅90=m⋅L
We can cancel m from both sides (assuming m≠0):
S⋅90=L
Rearranging the equation gives us:
SL=190
Thus, the ratio of the specific heat capacity of the liquid to the specific latent heat of fusion is:
SL=190
Topper's Solved these Questions
- HEAT TRANSFERBOOK - RESONANCE ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - Exercise-2
1 Videos
- HEAT TRANSFERBOOK - RESONANCE ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - Exercise-3
1 Videos
- HEAT TRANSFERBOOK - RESONANCE ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - Exercise-1
1 Videos
- GRAVITATIONBOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercise
21 Videos
- KINEMATICSBOOK - RESONANCE ENGLISHCHAPTER - KINEMATICSEXERCISE - Exercise
65 Videos
Similar Questions
Name the liquid which has the highest specific heat capacity.
View SolutionA rigid container of negligible heat capacity contains one mole of an ideal gas. The temperatures of the gas increases by 1∘C if 3.0 cal of heat is added to it. The gas may be
View SolutionA liquid X has the maximum specific heat capacity and is used as a coolant in car radiators. Name the liquid X.
View SolutionAn electric heater of power 150 W is immersed in 0.75 kg of ice at 0∘C in a lagged container of negligible heat capacity. The temperature remains constant for 27-5 minutes and then rises to 40−0∘C in a further 14 minutes. Explain why does the temperature remain constant. Calculate : (a) the specific latent heat of ice, and (b) the specific heat capacity of water.
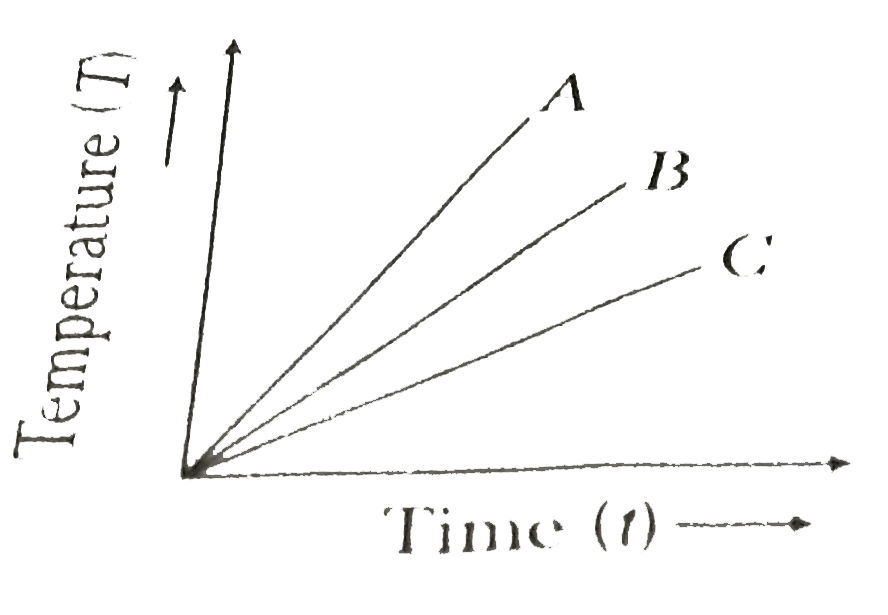
View SolutionThe temperatures versus time graph is shown in figure. Which of the substance A,B and C has the lowest heat capacity if heat is supplied to all of them at equal rates.
View SolutionThe temperature of 300 g of water at 40∘C is lowered to 0∘C by adding ice to it. Find the mass of ice added if specific heat capacity of water is 4.2 J g−1K−1 and specific latent heat of ice is 336 J g−1
View SolutionCalculate the amount of heat given out while 400 g of water at 30∘C is
cooled and converted into ice at −2∘C.
Specific heat capacity of water = 4200 J/kg K
Specific heat capacity of ice = 2100 J/ kg K
Specific latent heat of fusion of ice = 33600 J/kg
View SolutionTwo liquids of specific heat ratio 1:2 are at temperature 2θandθ
View Solution
Two bodies of equal masses are heated at a uniform rate under identical conditions. The change in temperature in the two cases in shown graphically. What are their melting points?
Find the ratio of their specific heats and latent heats.
View Solution104 g of water at 30∘C is taken in a calorimeter made of copper of mass 42 g. When a certain mass of ice at 0°C is added to it, the final steady temperature of the mixture after the ice has melted, was found to be 10∘C. Find the mass of ice added. [Specific heat capacity of water = 4.2 J g−1∘C−1, Specific latent heat of fusion of ice = 336 J g−1, Specific heat capacity of copper =0.4Jg−1∘C−1].
View Solution
