A block of weight is placed on a table. The table surface exerts an upward force of on the block. Assume .
The block exerts a force of on the table
The block exerts a force of on the table
The block exerts a force of on the table
The block has an upward acceleration.
The correct Answer is:A, D
To solve the problem, we need to analyze the forces acting on the block placed on the table.
1. Identify the Weight of the Block:
The weight of the block is given as W=9.8N. This weight acts downwards due to gravity.
2. Identify the Upward Force from the Table:
The table exerts an upward force (normal force) on the block, which is given as Fup=10N.
3. Apply Newton's Third Law of Motion:
According to Newton's Third Law, for every action, there is an equal and opposite reaction. Therefore, the block exerts a force on the table equal to the upward force it experiences.
- The block exerts a downward force of 10N on the table.
4. Determine the Net Force on the Block:
To find the net force acting on the block, we can subtract the weight of the block from the upward force:
Fnet=Fup−W=10N−9.8N=0.2N
Since the net force is positive, it indicates that the block is accelerating upwards.
5. Conclusion:
- The block exerts a force of 10N on the table.
- The block experiences an upward acceleration because the upward force exceeds its weight.
Summary of Options:
- Option 1: The block exerts a force of 10N on the table. (Correct)
- Option 2: The block exerts a force of 19.8N on the table. (Incorrect)
- Option 3: The block exerts a force of 9.8N on the table. (Incorrect)
- Option 4: The block has an upward acceleration. (Correct)
Final Answer:
The correct options are 1 and 4.
---
The weight of the block is given as W=9.8N. This weight acts downwards due to gravity.
The table exerts an upward force (normal force) on the block, which is given as Fup=10N.
According to Newton's Third Law, for every action, there is an equal and opposite reaction. Therefore, the block exerts a force on the table equal to the upward force it experiences.
- The block exerts a downward force of 10N on the table.
To find the net force acting on the block, we can subtract the weight of the block from the upward force:
Fnet=Fup−W=10N−9.8N=0.2N
Since the net force is positive, it indicates that the block is accelerating upwards.
- The block exerts a force of 10N on the table.
- The block experiences an upward acceleration because the upward force exceeds its weight.
- Option 1: The block exerts a force of 10N on the table. (Correct)
- Option 2: The block exerts a force of 19.8N on the table. (Incorrect)
- Option 3: The block exerts a force of 9.8N on the table. (Incorrect)
- Option 4: The block has an upward acceleration. (Correct)
The correct options are 1 and 4.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 246videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - TRUE/FALSE2videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 22.8videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise53videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
A block of mass 10kg is placed on a horizontal surface as shown in the figure and a force F=100N is applied on the block as shown, in the figure. The block is at rest with respect to ground. If the contact force between block and ground is 25n (in Newton) then value of n is : (Takeg=10m/s2)
 View Solution
View SolutionA block of mass 2 kg is placed on the floor. The coefficient of static friction it 0.4. A force F of 2.5 N is applied on the block, as shown. calculate the force of friction between the block and the floor. (g=9.8m/s2).
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass 2 kg is placed on the floor. The coefficient of static friction is 0.4. A force F of 2.5 N is applied on the block as shown in Fig. 15.4.4. The force of friction between the block and the floor is (g=9.8m/s2)
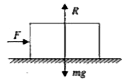 A1.5 NB0.5 NC2.5 NDNone of the above
A1.5 NB0.5 NC2.5 NDNone of the above
The sides of rectangular plate of mass 20 kg is 5 m x 4 m placed on a horizontal table. The pressure exerted by the block on the table is (Take g=10ms2)
View SolutionIn the figure, a block of weight 60N is placed on a rough surface. The coefficient of friction between the block and the surface is 0.5. The minimum weight of the block does not slip on the surface is (x×10)N. The value of x is
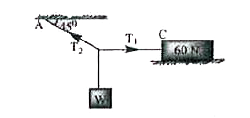 View Solution
View SolutionA block A of mass 4kg is kept on ground. The coefficient of friction between the block and the ground is 0.8. The external force of magnitude 30N is applied parallel to the ground. The resultant force exerted by the ground on the block is (g=10m/s2) a) 40 N b) 30 N c) zero d) 50 N
View SolutionA block of mass 10 kg is placed on the rough horizontal surface. A pulling force F is acting on the block which makes an angle θ above the horizontal. If coefficient of friction between block and surface is 43 then minimum value of force required to just move the block is (g=10ms2)
View SolutionA book of mass 5 kg is placed on a table and it is pressed by 10 N force then normal force exerted by the table on the book is
View SolutionA block of mass 2 kg is placed on the floor . The coefficient of static friction is 0.4 . If a force of 2.8 N is applied on the block parallel to floor , the force of friction between the block and floor is : (Taking g = 10m/s2)
View SolutionThree blocks of masses 5 kg, 3 kg and 2 kg are placed on a rough surface as shown in figure. Coefficient of friction between block and surface is same for all the blocks and is equal to μ=0.2 . A horizontal force of 15 N is applied on 5 kg block. The force exerted by 3 kg block on 2 kg block is : (g = 10 m/s2)
 View Solution
View Solution

