A block of mass 20 kg is acted upon by a force F=30N at an angle 53∘ with horizontal in downward direction as shown. The coefficient of friction between the block and the forizontal surface is 0.2. The friction force acting on the block by the ground is (g=10ms2)
40.0N
30.0N
18.0N
44.8N
The correct Answer is:C
To solve the problem step by step, we will analyze the forces acting on the block and calculate the frictional force.
Step 1: Identify the given values
- Mass of the block, m=20kg
- Applied force, F=30N
- Angle of applied force, θ=53∘
- Coefficient of friction, μ=0.2
- Acceleration due to gravity, g=10m/s2
Step 2: Calculate the weight of the block
The weight W of the block can be calculated using the formula:
W=m⋅g=20kg⋅10m/s2=200N
Step 3: Resolve the applied force into components
The applied force F has two components:
- Horizontal component:
Fx=F⋅cos(θ)=30N⋅cos(53∘)
Using cos(53∘)=35:
Fx=30⋅35=18N
- Vertical component:
Fy=F⋅sin(θ)=30N⋅sin(53∘)
Using sin(53∘)=45:
Fy=30⋅45=24N
Step 4: Calculate the normal force
The normal force N can be calculated by considering the vertical forces acting on the block. The normal force is equal to the weight of the block plus the vertical component of the applied force:
N=W+Fy=200N+24N=224N
Step 5: Calculate the maximum frictional force
The maximum frictional force fmax can be calculated using the formula:
fmax=μ⋅N=0.2⋅224N=44.8N
Step 6: Determine the actual frictional force
The actual frictional force f acting on the block will be equal to the horizontal component of the applied force, as long as it does not exceed the maximum frictional force:
f=Fx=18N
Since fmax(44.8N)>Fx(18N), the actual frictional force is:
f=18N
Final Answer
The friction force acting on the block by the ground is 18N.
- Mass of the block, m=20kg
- Applied force, F=30N
- Angle of applied force, θ=53∘
- Coefficient of friction, μ=0.2
- Acceleration due to gravity, g=10m/s2
The weight W of the block can be calculated using the formula:
W=m⋅g=20kg⋅10m/s2=200N
The applied force F has two components:
- Horizontal component:
Fx=F⋅cos(θ)=30N⋅cos(53∘)
Using cos(53∘)=35:
Fx=30⋅35=18N
Fy=F⋅sin(θ)=30N⋅sin(53∘)
Using sin(53∘)=45:
Fy=30⋅45=24N
The normal force N can be calculated by considering the vertical forces acting on the block. The normal force is equal to the weight of the block plus the vertical component of the applied force:
N=W+Fy=200N+24N=224N
The maximum frictional force fmax can be calculated using the formula:
fmax=μ⋅N=0.2⋅224N=44.8N
The actual frictional force f acting on the block will be equal to the horizontal component of the applied force, as long as it does not exceed the maximum frictional force:
f=Fx=18N
f=18N
The friction force acting on the block by the ground is 18N.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 34
Explore 5 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:DPP 35
Explore 5 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 32
Explore 8 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 53 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCE ENGLISHChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
A force of 100N is applied on a block of mass 3kg as shown below. The coefficient of friction between wall and the block is 1/4. The friction force acting on the block is :
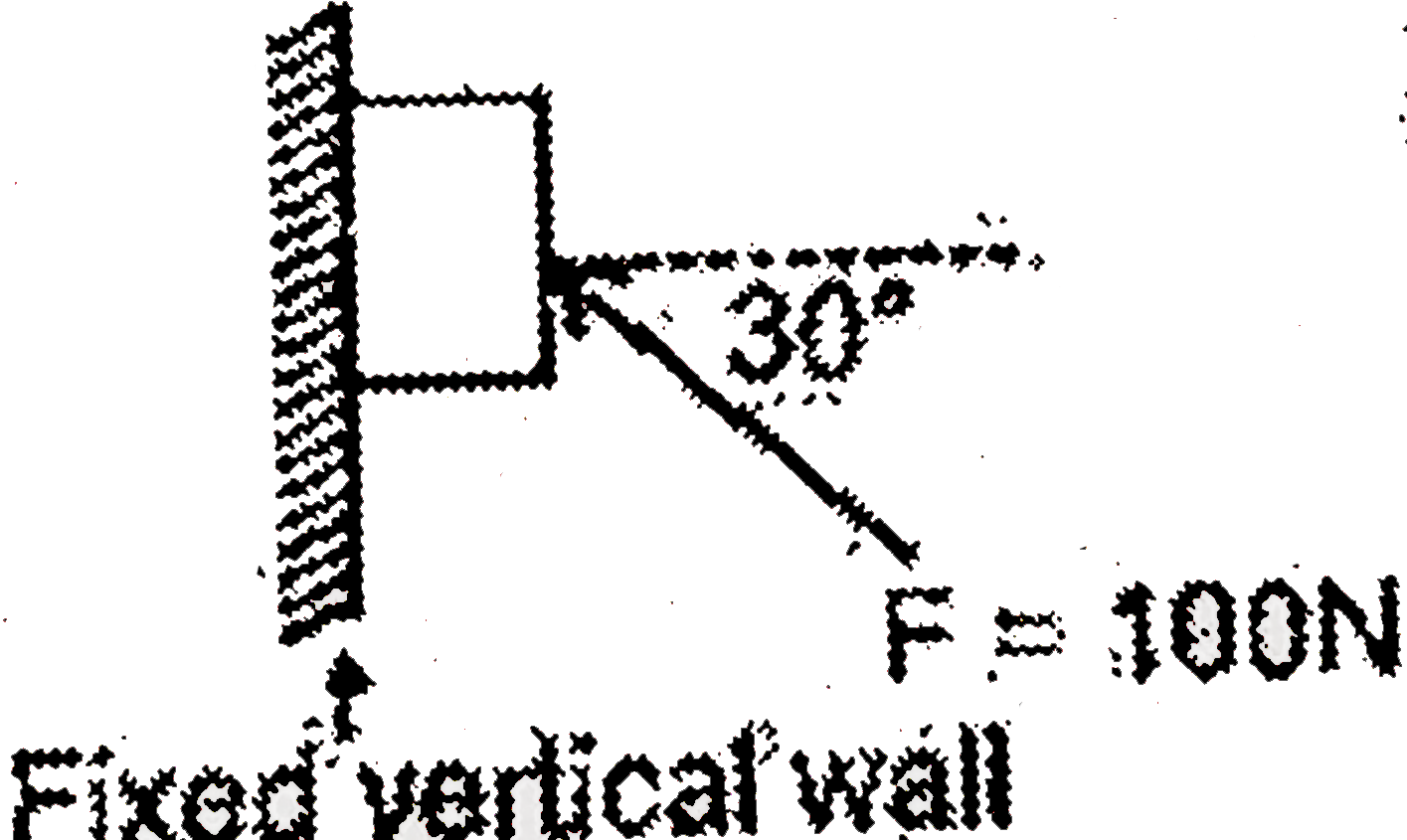
View SolutionA block of mass 8 kg is sliding on a surface inclined at an angle of 45∘ with the horizontal. Calculate the acceleration of the block. The coefficient of friction between the block and surface is 0.6. (Take g=10m/s2)
View Solution
Knowledge Check
A block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A10.3NB23.8NC11.9ND6.3NA block of mass 3 kg rests on a rough inclined plane making an angle of 30∘. With the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A9.8 NB0.7×9.8×√3 NC9.8×√3 ND0.7×9.8 N
A block of mass 8 kg is sliding on a surface inclined at an angle of 45∘ with the horizontal . Calculate the acceleration of the block . The coefficient of friction between the block and surface is 0⋅6 ( Take g = 10m/s2)
View SolutionA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
View SolutionA block of mass 1 kg is placed on a truck which accelerates with acceleration 5ms−2. The coefficient of static friction between the block and truck is 0.6. The frictional force acting on the block is
View SolutionA force of 200N is applied as shown in the figure on block of 3 kg. The coefficient of friction between the block and the wall is 0.3. Find the friction acting on the block. (in N) {Take g = 10 m/s2

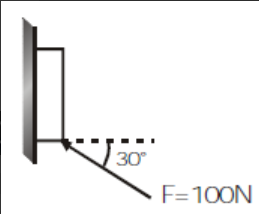
View SolutionA force of 100 N is applied on a block of mass 3 kg as shown in figure. The coefficient of friction between the surface and the block is 14 .Then the friction force acting on the block is
View SolutionA horizontal force of 10 N is necessary to just hold a block stationary against a wall. The coefficient of friction between the block and the wall is 0.2. the weight of the block is (g=10m/s2)

View Solution