
A block A (5kg) rests over another block B (3kg) placed over a smooth horizontal surface. There is friction between A and B. A horizontal force F1 gradually increasing from zero to a maximum is supplied to A so that the blocks move together without relative motion. Instead of this another horizontal force F2, gradually increasing from zero to a maximum is supplied to B so that the blocks move together without relative motion. Then
F1(max)=F2(max)
F1(max)>F2(max)
F1(max)<F2(max)
F1(max):F2(max)=5:3
The correct Answer is:B, D
(B,D) Case I:
Since, no relative motion :
a=F1−Ff5=Ff3⇒F1(max)=83Ff
Case II:
a=Ff5=F2−Ff3⇒F2(max)=85Ff
Clearly , F1(max)>F2(max) and F1(max)F2(max)=53
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 34
5 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - DPP 35
5 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 32
8 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
The coefficient of friction between block A of mass m1=5kg and block B of mass m2=10kg is μ2=0.5 . There is no friction froce between block B and fixed horizontal surface. A force of 300N acts on block B in horizontal direction and a horizontal force of magnitude F acts on block A as shown , both towards right. Initially there is no relative motion between the blocks. The minimum value of F such that relative motion starts between A and B is :
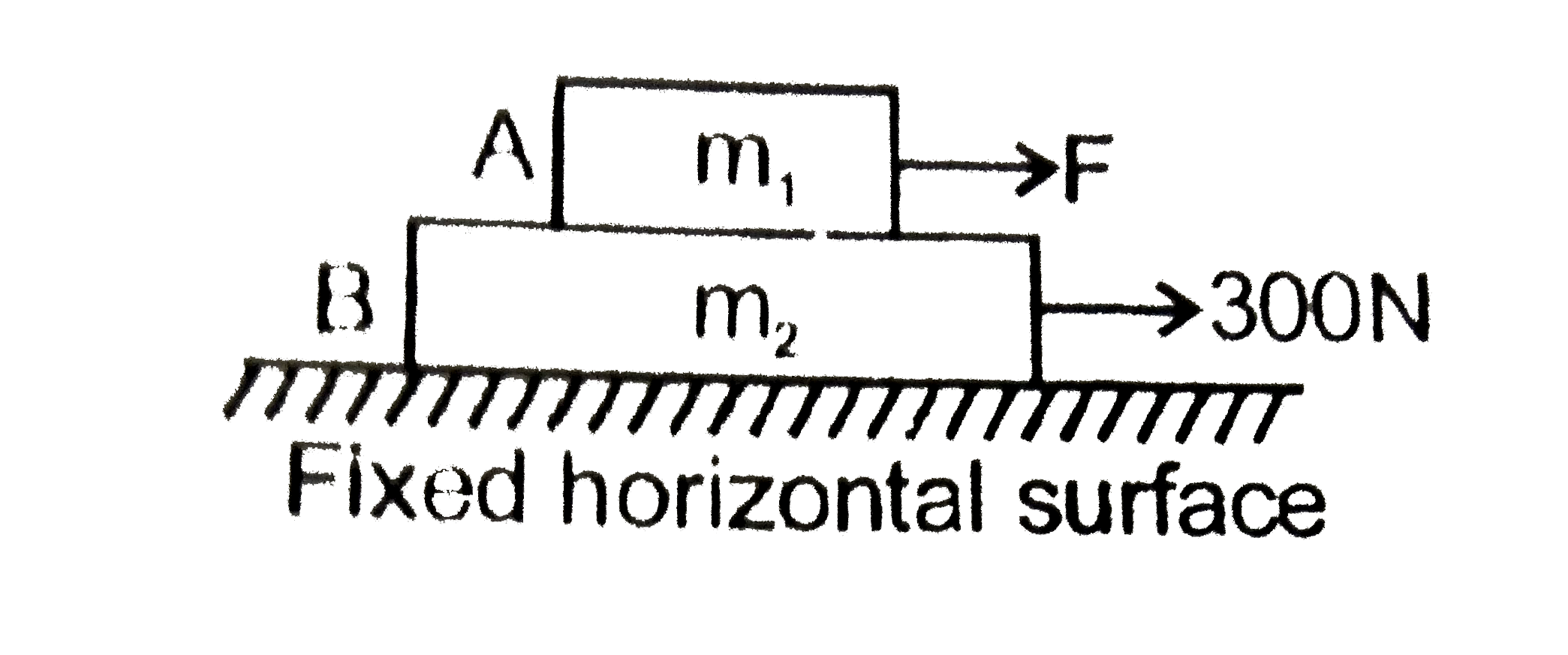
View SolutionWork done by static friction on an object
View SolutionA system is pushed by a force F as shown in figure All surfaces are smooth except between B and C is μ. Minimum value fo F to prevent block B from down ward slipping is

View SolutionSpecific resistance of a wire depends on the
View SolutionA wire loaded by a weight of density 7.8g/cc is found to be of length 100cm. On immersing the weight in water. The length decrease by 0.20 cm find the original length of the wire.
View SolutionA block A (5kg) rests over another block B (3kg) placed over a smooth horizontal surface. There is friction between A and B. A horizontal force F_1 gradually increasing from zero to a maximum is spplied to A so that the blocks move together without relative motion. Instead of this wanother horizontal force F_2 , gradually increasing from zero to a maximum is spplied to B so that the blocks move together without relative motion. Then
View SolutionIn the arrangement shown in figure, m_A = m_B = 2kg. String is massless and pulley is frictionless. Block B is resting on a smooth horizontal surface, while friction coefficient beteen block A and B is μ=0.5 . the Maximum horizontal force F that can be applied so that block A does not slip over block B is.

View SolutionThree blocks of masses 2kg,3kg and 5kg are placed in contact as shown in the diagram. A horizontal force of 30N is applied on 2kg block. Find the contact force between (a) 2kg and 3kg block and (b) 3kg and 5kg block.
View SolutionBlock B of mass m has been placed on block A of mass 3 m as shown. Block A rests on a smooth horizontal table. F1 is the maximum horizontal force that can be applied on the block A such that there is no slipping between the blocks. Similarly, F2 is the maximum horizontal force that can be applied on the block B so that the two blocks move together without slipping on each other. When F1andF2 both are applied together as shown in figure.

(a) Find the friction force acting between the blocks.
(b) Acceleration of the two blocks.
(c) If F2 is decreased a little, what will be direction of friction acting on B.
View SolutionA block of mass m is placed on a rough horizontal surface. The coefficent of friction between them is μ. An external horizontal force is applied to the block and its magnitude is gradually increased. The force exerted by the block on the surface is R.
View SolutionTwo block A and B of masses 5 kg. and 3 kg. respectively rest on smooth horizontal surface with B over A. The coefficient of friction between A and B. 0.5 the maximum horizontal force that can be applied to A so that there will be motion of A and B without separation is :-
View SolutionTwo blocks A and B are placed one over the other on a smooth horizontal surface. The maximum horizontal force that can be applied on the lower block A, so that A and B move without separation is 49N. The coefficient of friction between A and B is (take g = 9.8ms−2 )
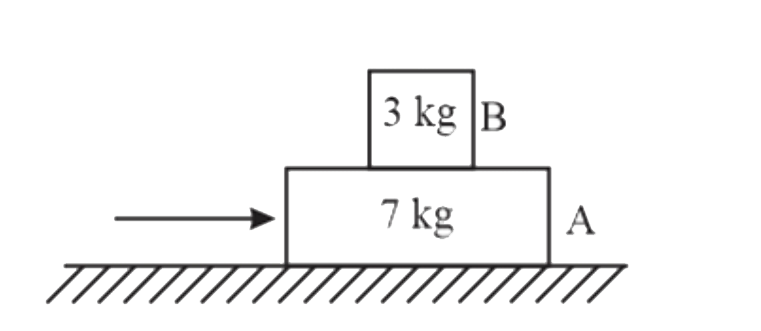
View SolutionBlock A of mass 2 kg is placed over block B of mass 8 kg .The combination is placed over a rough horizonatal surface .Cofficient of friction between B and the floor is 0.5 .Coefficient of friction berween A and B is 0.4 .A horizontal force of 10 N is applied on block B .The force of friction between A and B is
(g=10 ms−2)
View SolutionA block A of mass 4 kg is placed on another block B of mass 5 kg, and the block B rests on a smooth horizontal table. If the minimum force that can be applied on A so that both the blocks move together is 12N, the maximum force that can be applied on B for the blocks to move together will be:
View SolutionA block A of mass 4 kg is placed on another block B of mass 5 kg, and the block B rests on a smooth horizontal table. If the minimum force that can be applied on A so that both the blocks move together is 12N, the maximum force that can be applied on B for the blocks to move together will be:
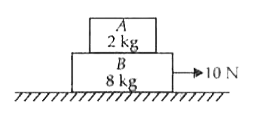
View SolutionA 2kg block is placed over a 4kg block and both are placed on a smooth horizontal surface. The coefficient of friction between the blocks is 0.20. The acceleration of the two blocks if a horizontal force of 12N is applied to the lower block is
View Solution
