One end of massless inextensible string of length l is fixed and other end is tied to a small ball of mass m. The ball is performing a circular motion in vertical plane. At the lowest position, speed of ball is √20gl. Neglect any other forces on the ball except tension and gravitational force. Acceleration due to gravity is g.
At the highest position of ball, tangential acceleration of ball is −
0
g
5g
16g
The correct Answer is:A
To find the tangential acceleration of the ball at the highest position in its circular motion, we can follow these steps:
Step 1: Understand the problem
We have a ball of mass m attached to a massless, inextensible string of length l. The ball is performing circular motion in a vertical plane. At the lowest position, the speed of the ball is given as \( v = \sqrt{20gl} \).
Step 2: Use the conservation of energy
At the lowest point, the potential energy (PE) is zero, and the kinetic energy (KE) is given by:
\(
KE_{low} = \frac{1}{2} m v^2 = \frac{1}{2} m (20gl) = 10 mgl
\)
At the highest point, the height of the ball is \( 2l \), so the potential energy at the highest point is:
\(
PE_{high} = mgh = mg(2l) = 2mgl
\)
Let \( v_{high} \) be the speed of the ball at the highest point. The kinetic energy at the highest point is:
\(
KE_{high} = \frac{1}{2} m v_{high}^2
\)
By the conservation of mechanical energy:
\(
KE_{low} = KE_{high} + PE_{high}
\)
Substituting the values:
\(
10 mgl = \frac{1}{2} m v_{high}^2 + 2mgl
\)
Step 3: Solve for \( v_{high} \)
Rearranging the equation:
\(
10 mgl - 2mgl = \frac{1}{2} m v_{high}^2
\)
\(
8 mgl = \frac{1}{2} m v_{high}^2
\)
Dividing both sides by \( m \):
\(
8gl = \frac{1}{2} v_{high}^2
\)
Multiplying by 2:
\(
16gl = v_{high}^2
\)
Taking the square root:
\(
v_{high} = \sqrt{16gl} = 4\sqrt{gl}
\)
Step 4: Find the centripetal acceleration
At the highest point, the forces acting on the ball are the gravitational force \( mg \) acting downward and the tension \( T \) in the string also acting downward. The net force towards the center (which provides centripetal acceleration) is:
\(
F_{net} = mg + T
\)
This net force must equal the centripetal force:
\(
F_{net} = \frac{mv_{high}^2}{l}
\)
Substituting \( v_{high}^2 \):
\(
mg + T = \frac{m(16gl)}{l}
\)
Simplifying:
\(
mg + T = 16mg
\)
Thus:
\(
T = 16mg - mg = 15mg
\)
Step 5: Determine the tangential acceleration
Tangential acceleration is related to the change in speed along the path of motion. At the highest point, the only forces acting are the gravitational force and tension, and since the ball is moving in a circular path, there is no net force acting tangentially to the motion. Therefore, the tangential acceleration is:
\(
a_{tangential} = 0
\)
Final Answer
The tangential acceleration of the ball at the highest position is \( 0 \).
---
We have a ball of mass m attached to a massless, inextensible string of length l. The ball is performing circular motion in a vertical plane. At the lowest position, the speed of the ball is given as \( v = \sqrt{20gl} \).
At the lowest point, the potential energy (PE) is zero, and the kinetic energy (KE) is given by:
\(
KE_{low} = \frac{1}{2} m v^2 = \frac{1}{2} m (20gl) = 10 mgl
\)
\(
PE_{high} = mgh = mg(2l) = 2mgl
\)
\(
KE_{high} = \frac{1}{2} m v_{high}^2
\)
\(
KE_{low} = KE_{high} + PE_{high}
\)
Substituting the values:
\(
10 mgl = \frac{1}{2} m v_{high}^2 + 2mgl
\)
Rearranging the equation:
\(
10 mgl - 2mgl = \frac{1}{2} m v_{high}^2
\)
\(
8 mgl = \frac{1}{2} m v_{high}^2
\)
Dividing both sides by \( m \):
\(
8gl = \frac{1}{2} v_{high}^2
\)
Multiplying by 2:
\(
16gl = v_{high}^2
\)
Taking the square root:
\(
v_{high} = \sqrt{16gl} = 4\sqrt{gl}
\)
At the highest point, the forces acting on the ball are the gravitational force \( mg \) acting downward and the tension \( T \) in the string also acting downward. The net force towards the center (which provides centripetal acceleration) is:
\(
F_{net} = mg + T
\)
This net force must equal the centripetal force:
\(
F_{net} = \frac{mv_{high}^2}{l}
\)
Substituting \( v_{high}^2 \):
\(
mg + T = \frac{m(16gl)}{l}
\)
Simplifying:
\(
mg + T = 16mg
\)
Thus:
\(
T = 16mg - mg = 15mg
\)
Tangential acceleration is related to the change in speed along the path of motion. At the highest point, the only forces acting are the gravitational force and tension, and since the ball is moving in a circular path, there is no net force acting tangentially to the motion. Therefore, the tangential acceleration is:
\(
a_{tangential} = 0
\)
The tangential acceleration of the ball at the highest position is \( 0 \).
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 70
7 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 71
8 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 69
5 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
One end of massless inextensible string of length l is fixed and other end is tied to a small ball of mass m. The ball is performing a circular motion in vertical plane. At the lowest position, speed of ball is √20gl. Neglect any other forces on the ball except tension and gravitational force. Acceleration due to gravity is g.
Motion of ball is in nature of
View SolutionOne end of massless inextensible string of length l is fixed and other end is tied to a small ball of mass m. The ball is performing a circular motion in vertical plane. At the lowest position, speed of ball is √20gl. Neglect any other forces on the ball except tension and gravitational force. Acceleration due to gravity is g.
During circular motion, minimum value of tension in the string−
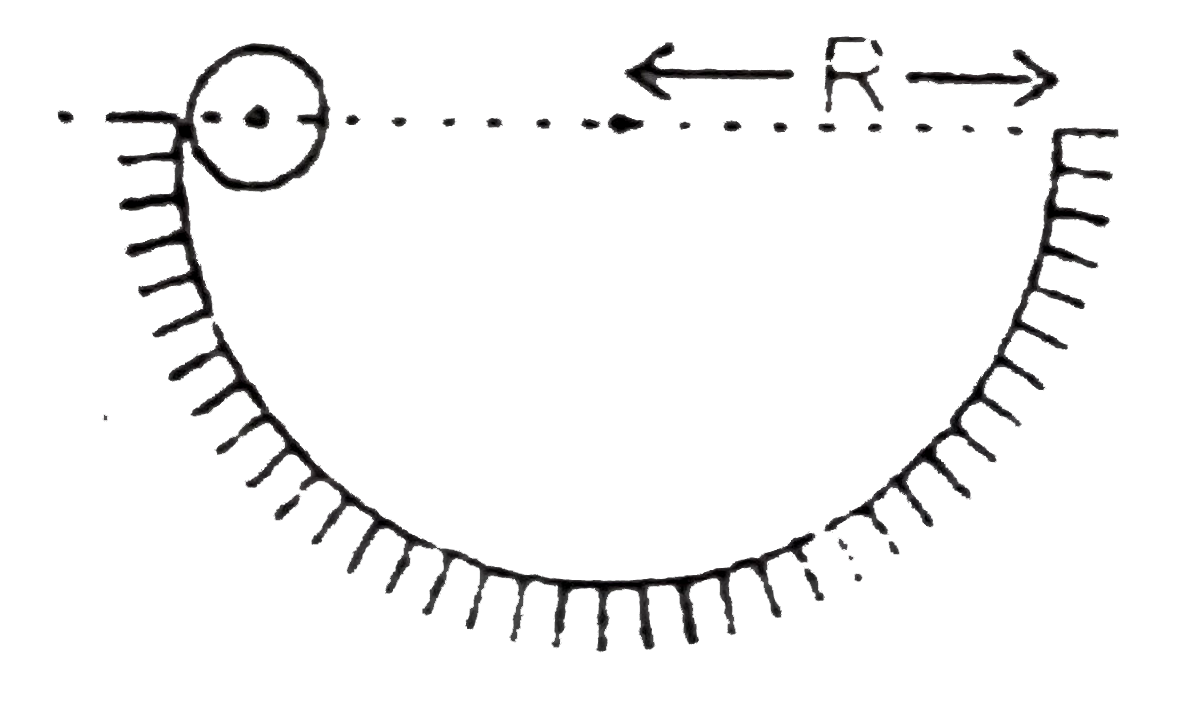
View SolutionIn the figure shown, a small ball of mass 'm' can move witgout sliding in a fixed semicircular track of radius R in vertical planet. It is released from the top. The resultant force on the ball at the lowest of the track is
View SolutionA particle is moving in a circular path in the vertical plane. It is attached at one end of a string of length l whose other end is fixed. The velocity at lowest point is u . The tension in the string T and acceleration of the particle is a at any position. Then T.a is zero at highest point if
View SolutionA particle is moving in a circular path in the vertical plane. It is attached at one end of a string of length l whose other end is fixed. The velocity at lowest point is u. The tension in the string is T and acceleration of the particle is a at any position then T. a' is positive at the lowest point for
View SolutionA massless spring of length l and spring constant k is placed vertically on a table. A ball of mass m is just kept on top of the spring. The maximum velocity of the ball is
View SolutionA ball tied to the end of the string swings in a verticla plane in a vertical circle under the influence of gravity.
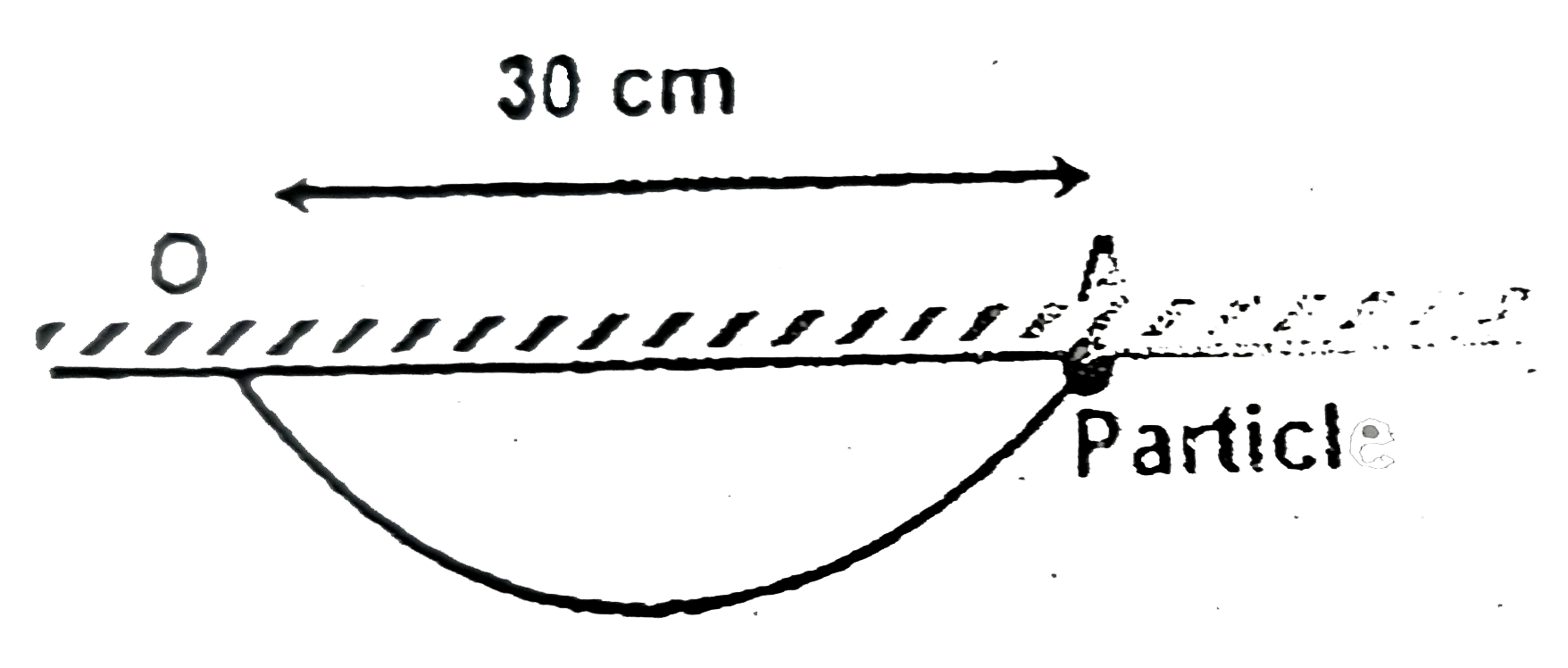
View SolutionA small ball of mass 100g is attached to a light and inextensible string of length 50cm. The string is tied to a support O and the mass m released from point A which is a' a horizontal distance of 30cm from the support. Calculate the speed of the ball is its lowest point of the trajectory.
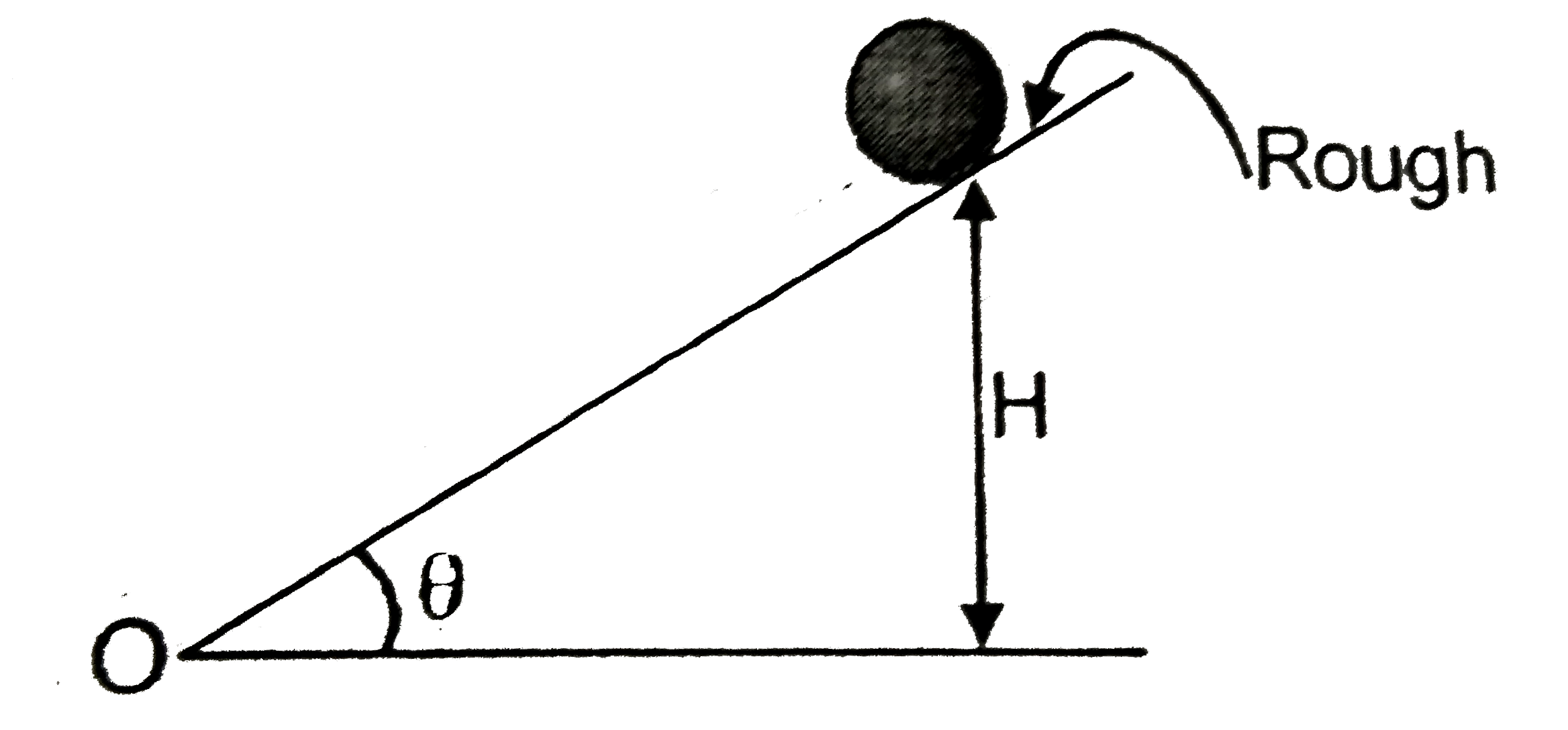
View SolutionA solid ball of mass 'm' is released on a rough fixed inclined plane from height H. The ball will perform pure rolling on the inclined plane. Then
View SolutionA ball of mass 0.2 kg moves with a velocity of 20m/sec and it stops in 0.1 sec , then the force on the ball is
View Solution
