A uniform disc of mass 300 kg is rotating freely about a vertical axis through its centre at a constant angular velocity ω0. A boy of mass 30 kg starts from the centre and moves along a radius to the edge of the disc. Angular velocity of the disc ill now become
ω06
ω05
4ω05
5ω06
The correct Answer is:D
As Στ=0 , angular momentum remains conserved :
∴L=(0+300R22)
ω0=(300R22+30R2).ω
=150ω0=180ω
⇒ω=56ω0Ans.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - comprehension127videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 707videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 687videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise53videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
A uniform disk of mass 300kg is rotating freely about a vertical axis through its centre with constant angular velocity ω. A boy of mass 30kg starts from the centre and moves along a radius to the edge of the disk. The angular velocity of the disk now is
View SolutionA uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same mass m and having velocity of 2ωR towards centre of the disc collides with the disc moving horizontally and sticks to its rim. Then
View SolutionA solid sphere of radius r and mass m rotates about an axis passing through its centre with angular velocity ω. Its K.E. Is
View SolutionA man of mass m stands on a horizontal platform in the shape of a disc of mass m and radius R, pivoted on a vertical axis thorugh its centre about which it can freely rotate. The man starts to move aroung the centre of the disc in a circle of radius r with a velocity v relative to the disc. Calculate the angular velocity of the disc.
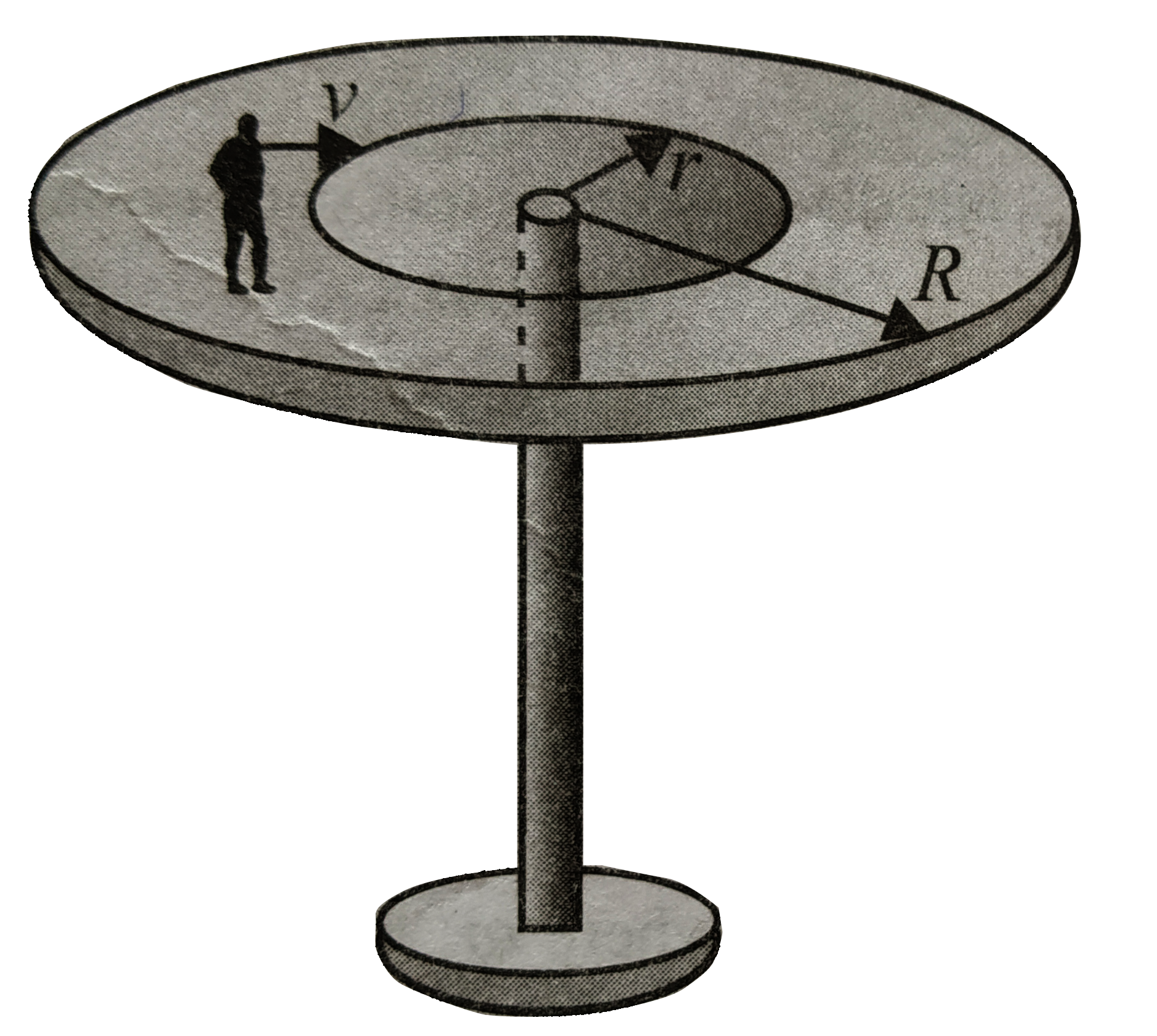 View Solution
View SolutionA uniform disc of mass m and radius R is rotated about an axis passing through its center and perpendicular to its plane with an angular velocity ω. It is placed on a rough horizontal plane with the axis of the disc keeping vertical. Coefficient of friction between the disc and the surface is μ, find
(a). The time when disc stops rotating
(b). The angle rotated by the disc before stopping.View SolutionA horizontal disc is rotating about a vertical axis passing through its centre. If an insect moves from centre to rim then the angular momentum of the system
View SolutionA uniform horizontal circular platform of mass 200kg is rotating at 5 rpm about vertical axis passing through its centre. A boy of mass 80kg is standing at its edge. if boy moves to centre of platform, find out final angular speed
View SolutionA thin horizontal circular disc is roating about a vertical axis passing through its centre. An insect is at rest at a point near the rim of the disc. The insect now moves along a diameter of the disc to reach its other end. During the journey of the insect, the angular speed of the disc.
View SolutionA horizontally oriented uniform disc of mass M and radius R rotates freely about a stationary vertical axis passing through its centre. The disc has a radial guide along which can slide without friction a small body of mass m. A light thread running down through the hollow axle of the disc is tied to the body initially the body was located at the edge of the disc and the whole system rotated with ann angular velocity ω0. Then by means of a force F applied to the lower and of the thread the body was slowly pulled to the rotation axis. find:
(a). The angular velocity of the system in its final state.
(b). The work performed by the force F.View Solution
A uniform disc of mass M and radius R is pivoted about the horizontal axis through its centre C A point mass m is glued to the disc at its rim, as shown in figure. If the system is released from rest, find the angular velocity of the disc when m reaches the bottom point B.View Solution

