The uniform solid sphere shown in the figure has a spherical hole in it. Find the position of its centre of mass.
The correct Answer is:I=57140MR2

ρ=M(4/3)πR3−(4/3)π(R/2)3
I=25MR2−(25M2(R2)2+M2(R2)2)
,I=57140MR2
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 59
5 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 60
5 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 57
7 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
The objects in the figure are constructed of uniform wire bent into the shape shown. Find the position of the position of the centre of mass of each shape.

View SolutionThe object shown in figure is constructed of uniform rods of same material. Find the position of centre of mass w.r.t. its corner O.

View SolutionA circular plate of uniform thickness has a diameter fo 56cm. A circular portion of diameter 42 cm is removed from one edge of the plate as shown in figure. Find the position of the centre of mass of the remaining portion.

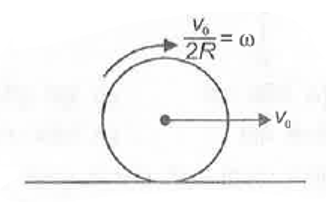
View SolutionA solid sphere has combined linear and rotation motion as shown in figure. The velocity of its centre of mass when it starts pure rolling is (R = radius of sphere)
View SolutionA solid sphere has combined linear and rotation motion as shown in figure. The velocity of its centre of mass when it starts pure rolling is (R = radius of sphere)
View SolutionA solid sphere of radius R is rolled by a force F acting at the topo of the sphere as shown in the figure. There is no slipping and initially sphere is in the rest position, then (CM= centre of mass)

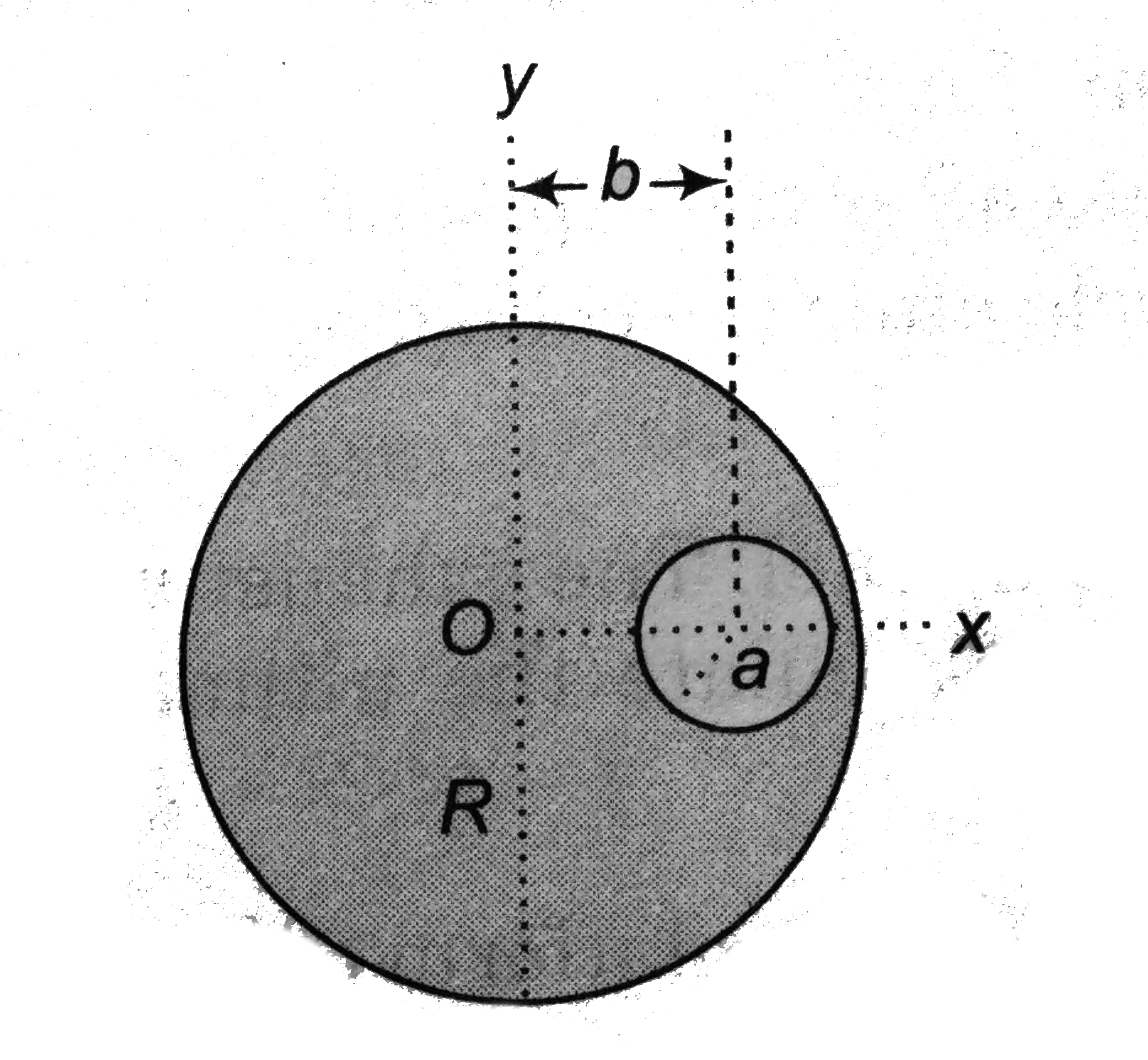
View SolutionA hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . They y -coordinate of the centre of mass of the remaining sphere is

View SolutionTwo uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O

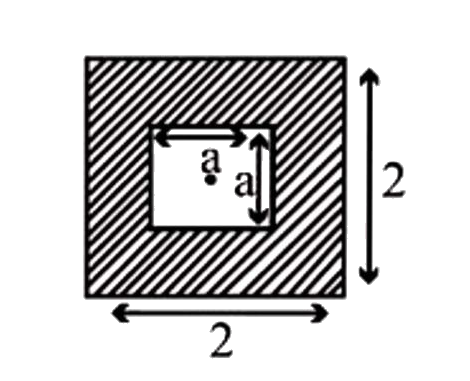
View SolutionA square of a side a is cut from a square of side 2a as shown in the figure. Mass of this square with a hole is M. Then its moment of inertia about an axis passing through its centre of mass and perpendicular to its plane will be
View SolutionFrom a uniform disc of radius R, an equilateral triangle of side √3R is cut as shown in the figure. The new position of centre of mass is :

View Solution
