From a uniform disc of radius R, an equilateral triangle of side √3R is cut as shown in the figure. The new position of centre of mass is :

(0,0)
(0,R)
(0,√3R2)
none of these
The correct Answer is:B
m1 = mass of remaining part.
m2 = mass of cut part and y1y2cm of m1m2
respectively for complete system, we have
ycm=m1y1+m2y2(m1+m2) (with respect to centre of the circle, ycm=0 moreover centre of mass of the Δ is also at this centre of the circle, so y2 is also 0.
0=σ(πR2−3R√34)y1+σ3R2√34×(0)σ(πR2)⇒y1=0so(0,0).

Topper's Solved these Questions
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - LEVEL - 2 PARAGRAPH QUESTIONS
2 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE MAIN (ARCHIVE)
53 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - Level - 1 PARAGRAPH QUESTIONS
3 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)
89 Videos
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )
111 Videos
Similar Questions
Find the coordinates of the vertices of an equilateral triangle of side 2a as shown in Figure.
View SolutionThe figure shows a disc of radius 3R from which a circular hole of radius R is cut as shown in the figure. The distance of the centre of mass of the remaining object from the point O is
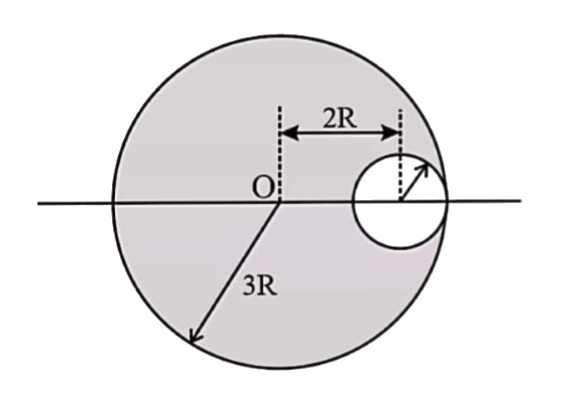
View Solution
Knowledge Check
From a uniform circular disc of radius R and mass 9M, a small disc of radius R3 is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is :
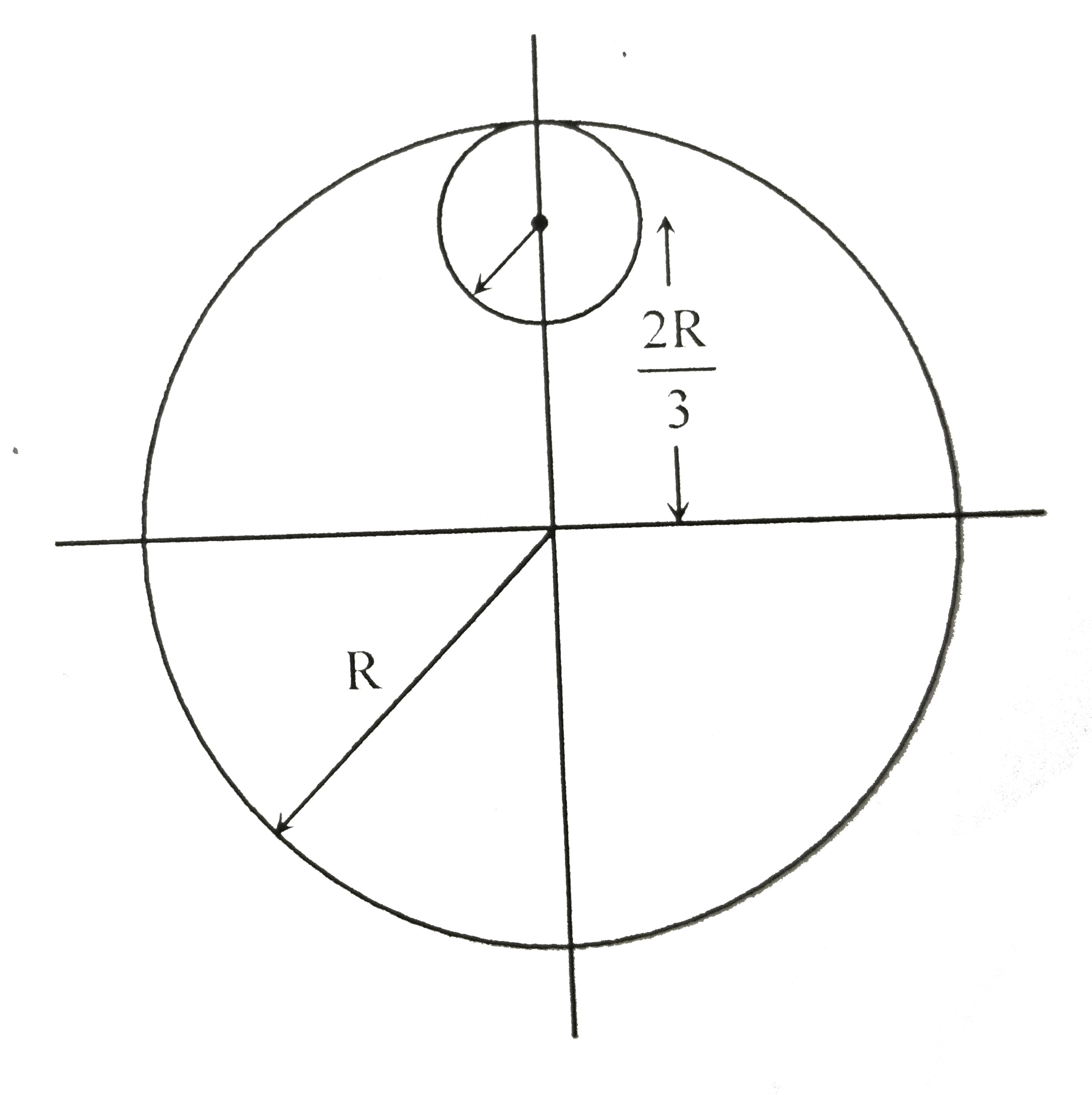 A4MR2B409MR2C40MR2D379MR2
A4MR2B409MR2C40MR2D379MR2
A uniform disc of mass M and radius R is liffted using a string as shown in the figure. Then choose incorrect option(s),

View SolutionThe distance of center of mass from the center of a uniform disc of radius R. if a circular plate is removed from the disc as shown in figure will be (C is centre of complete disc)
View SolutionWhat will be the position of centre of mass of a half disc shown ?
 .
.
View SolutionFrom a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulting flat body.
View SolutionFrom a circular disc of radius R, a triangular portion is cut (sec figure). The distance of the centre of mass of the remainder from the centre of the disc is −

View SolutionA uniform disc of mass m and radius r and a point mass m are arranged as shown in the figure. The acceleration of point mass is :( Assume there is no slipping between pulley and thread and the disc can rotate smoothly about a fixed horizontal axis passing through its centre and perpendicular to its plane )

View SolutionA loop in the shape of an equilateral triangle triangle of side a carries a current I as shown in the figure.Find out the magnetic field at the centre C of the triangle.
View Solution
