In the figure (i) a disc of mass M(kg) and radius R(m) is rotating smoothly about a fixed vertical axis AB with angular speed 26rad/s A rod rod CD of length R2(m) and mass M(kg) is hinged at one end at point 'D' on the disc. The rod remains in vertical position and rotates along with the disc about axis AB. At some moment the rod CD gets a very smal impulse at point 'C' due to air due to which the rod falls on the disc along one radius and sticks to the disc as shown in figure (ii). Now find the angular velocity of the disc in rad/s.

The correct Answer is:36
MI of the system when rod is vertical
I=12mR3+mR2
MI of system when rod is horizontal
I'=12mR2+⎡⎢
⎢
⎢⎣m(R2)212+m(3R4)2⎤⎥
⎥
⎥⎦
=1312mR2
from conservation of angular momentum of system about axis AB is
Iω=I'ω'
or ω'=32mR2ω1312mR2=1813ω
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - DPP 655videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 664videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 635videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise53videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
A bar of mass M and length L is in pure traslatory motion with its of mass velocity V . It collides with and sticks to a second identical bar which is initially at rest . ( Assume that it bocomes one composite bar of length 2L). The angular velocity of the composite bar will be
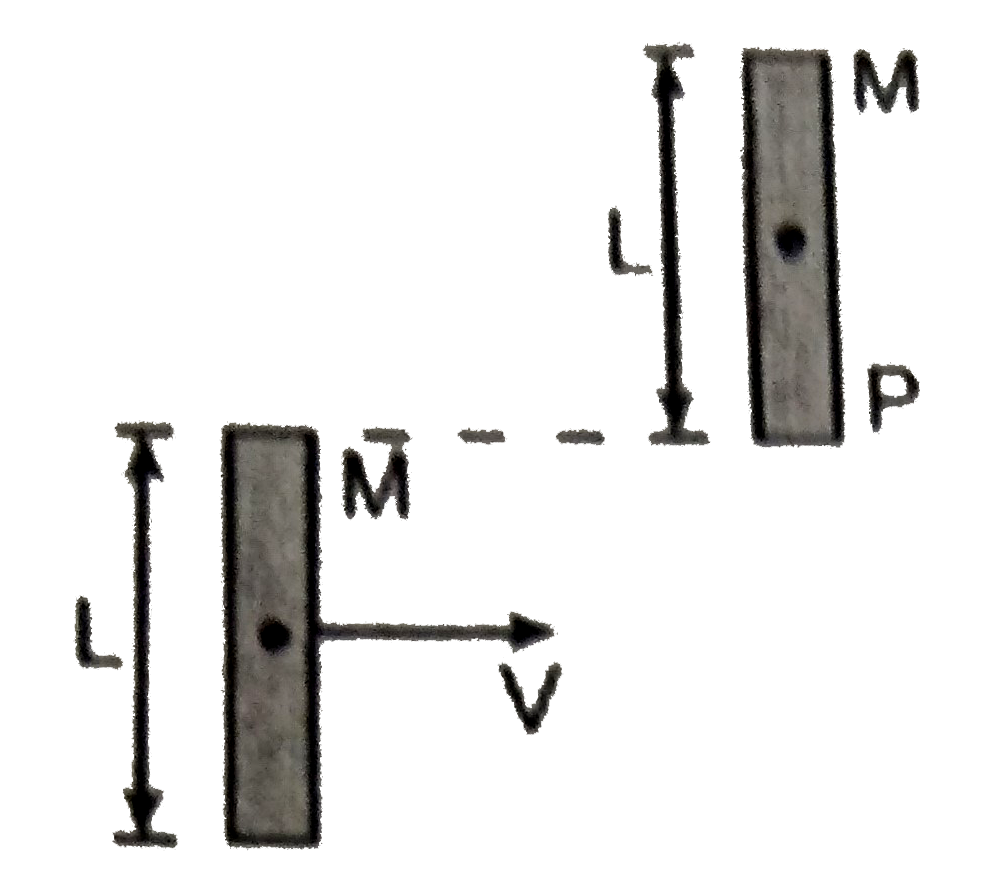 06:28View Solution
06:28View SolutionA ring and a disc of same mass m and same radius R are joinged concentrically. This system is placed on a smooth plane with the common axis parallel to the plane as shown in figure. A horizontal force F is applied on the system at a point which is at a distance x from the centre. The value of x so that it starts pure rolling is
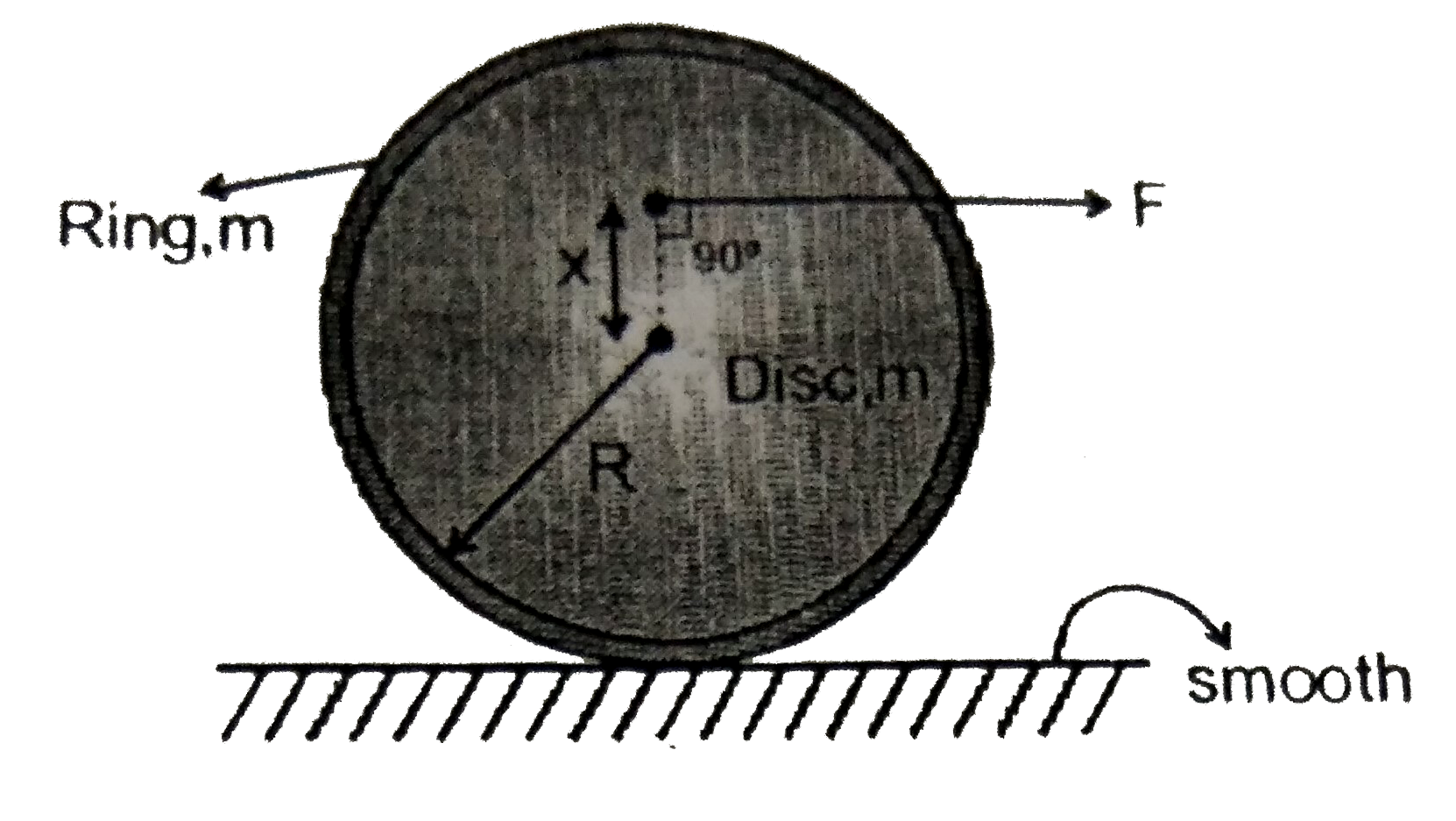 02:22View Solution
02:22View SolutionA uniform disc of mass m and radius r and a point mass m are arranged as shown in the figure. The acceleration of point mass is :( Assume there is no slipping between pulley and thread and the disc can rotate smoothly about a fixed horizontal axis passing through its centre and perpendicular to its plane )
 06:27View Solution
06:27View SolutionSpecific resistance of a wire depends on the
04:28View SolutionA wire loaded by a weight of density 7.8g/cc is found to be of length 100cm. On immersing the weight in water. The length decrease by 0.20 cm find the original length of the wire.
02:12View SolutionTwo point masses of 0.3 kg and 0.7kg are fixed at the ends of a rod of length 1.4 m and of negligible mass. The rod is set rotating about an axis perpendicular to its length with a uniform angular speed. The point on the rod through which the axis should pass in order that the work required for rotation of the rod is minimum, is located at a distance of
View Solution
A rod of mass 2 kg ad length 2 m is rotating about its one end O wth an angular velocity ω=4rad/s. Find angular momentum of the rod about the axis rotation.03:18View SolutionA conical pendulum, a thin uniform rod of length l and mass m , rotates uniformly about a vertical axis with angular velocity omega (the upper end of the rod is hinged). Find the angle theta between the rod and the vertical.
04:25View SolutionIn the figure (i) a disc of mass M(kg) and radius R(m) is rotating smoothly about a fixed vertical axis AB with angular speed 26 rad//s A rod rod CD of length (R)/(2)(m) and mass M(kg) is hinged at one end at point 'D' on the disc. The rod remains in vertical position and rotates along with the disc about axis AB . At some moment the rod CD gets a very smal impulse at point 'C' due to air due to which the rod falls on the disc along one radius and sticks to the disc as shown in figure (ii) . Now find the angular velocity of the disc in rad//s .
09:10View SolutionA uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle theta with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:
05:16View SolutionA uniform disc of mass M and radius R is rotating freely about its central vertical axis with angular speed w0. Another disc of mass m and radius r is free to rotate about a horizontal rod AB. Length of the rod AB isL(<R) and its end A is rigidly attached to the vertical axis of the first disc. The disc of mass m, initially at rest, is placed gently on the disc of mass M as shown in figure. Find the time after which the slipping between the two discs will cease. Assume that normal reaction between the two discs is equal to mg. Coefficient of friction between the two discs is μ.
 View Solution
View SolutionA uniform rod of mass m and length L lies radialy on a disc rotating with angular speed ω in a horizontal plane about vertical axis passing thorugh centre of disc. The rod does not slip on the disc and the centre of the rod is at a distance 2L from the centre of the disc. them the kinetic energy of the rod is
 View Solution
View SolutionA mechanism consists of a part which is translated with a velocity u and a rod AB of length L and mass M hinged at A The rod rotates about axis A with angular velocity omega the kinetic energy of rod when it is vertical as shown is
03:15View SolutionA rod of mass m and length 2R can rotate about an axis passing through O invertical plane.A disc of mass m and radius R//2 is hinged to the other end P ofthe rod and can freely rotate about P. When disc is at lowest point both rod and disc has angular velocity omega . If rod rotates by maximum angle theta=60^(@) with downward vertical, then omega interms of R and g will be(all hinges are smooth)
01:53View SolutionA rod PQ of mass m and length L is rotated about an axis through P as shown in figure. Find the moment of inertia of the rod about the axis of rotation.
 03:13View Solution
03:13View Solution

