Question

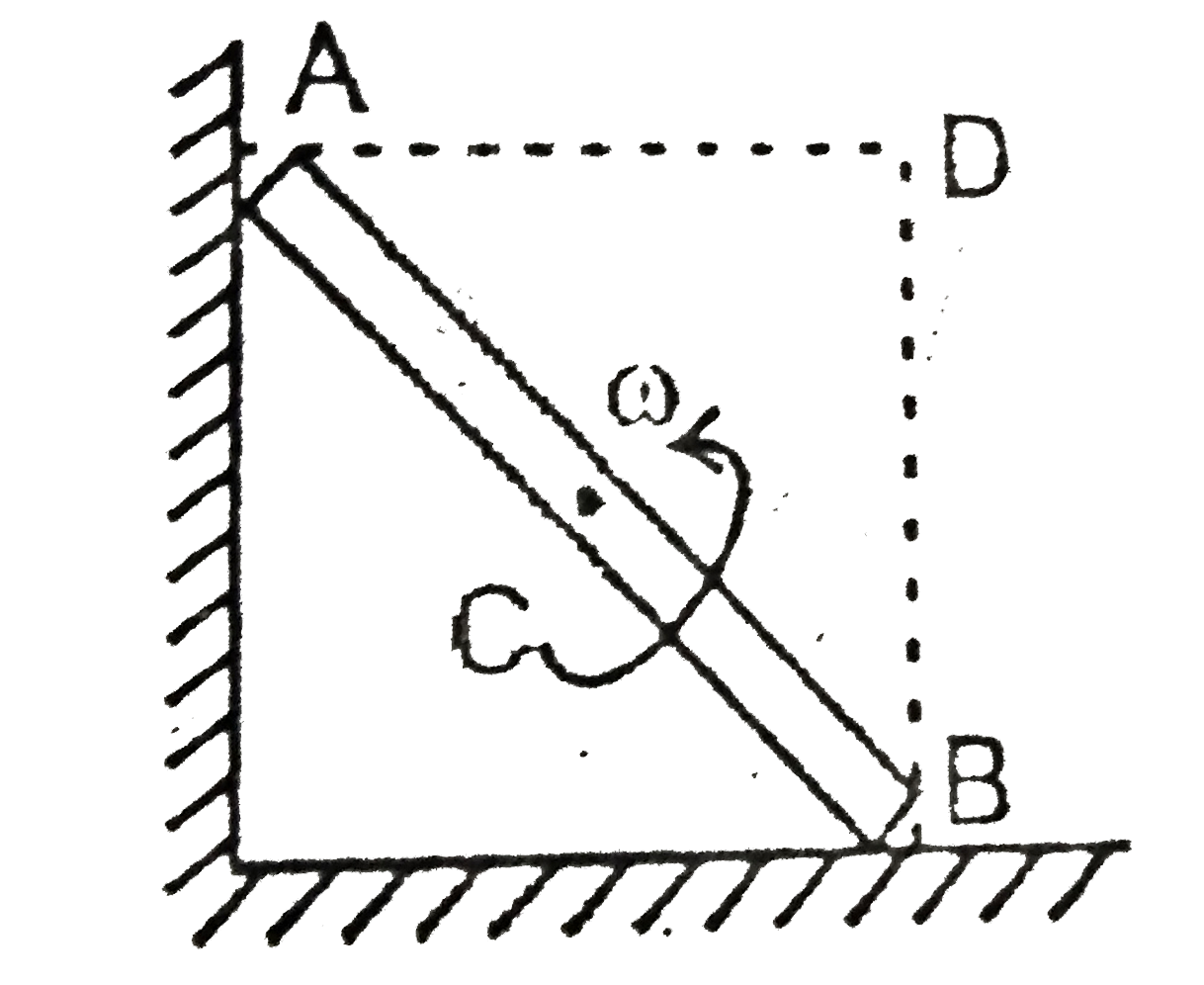
A thin uniform rod $AB$ is sliding between two fixed right angled surfaces. At some instant its angular velocity is $\omega$. If $I_x$ represent moment of inertia of the rod about an axis perpendicualr to the plane and passing through the point $X(A,B,C,\text{or}D)$, the kinetic energy of the rod is

Options

A. `(1)/(2)I_(A)omega^(2)`
B. `(1)/(2)I_(B)omega^(2)`
C. `(1)/(2)I_(C)omega^(2)`
D. `(1)/(2)I_(D)omega^(2)`

Answer

A::B::D

Explanation

(Tough) The point `D` is the instantaneous centre of rotation.
`K.E. =(1)/(2)I_(D) omega^(2)=(1)/(2)I_(A)omega^(2)=(1)/(2)I_(B)omega^(2)`