A solide homogeneous cylinder of height h and base radius r is kept vertically on a conveyer belt moving horizontally with an increasing velocity v=a+bt2. If the cylinder is not allowed to slip then the time whem the cylinder is about to topple , will be equal to
rgbh
2rgbh
2bgrh
rg2bh
The correct Answer is:A
To solve the problem, we need to determine the time at which a solid homogeneous cylinder, placed on a conveyor belt with an increasing velocity, is about to topple. Here’s a step-by-step solution:
Step 1: Understand the Motion of the Cylinder
The cylinder is on a conveyor belt that moves horizontally with a velocity given by the equation:
v=a+bt2
where a and b are constants, and t is time.
Step 2: Determine the Acceleration
To find the acceleration of the cylinder, we differentiate the velocity with respect to time:
a=dvdt=ddt(a+bt2)=2bt
Thus, the acceleration a of the cylinder is:
a=2bt
Step 3: Analyze Forces Acting on the Cylinder
When the cylinder is about to topple, we need to consider the forces acting on it:
- The weight of the cylinder mg acts downward at its center of mass.
- The normal force N acts upward at the base of the cylinder.
- A pseudo force Fpseudo=ma acts horizontally in the opposite direction of the acceleration of the belt.
Step 4: Set Up the Torque Equation
For the cylinder to be in equilibrium just before toppling, the torque about the point of contact (point P) must be balanced. The torque due to the weight of the cylinder and the torque due to the pseudo force must be equal.
The torque due to the weight mg about point P is:
τweight=mg⋅r
where r is the radius of the cylinder.
The torque due to the pseudo force ma about point P is:
τpseudo=ma⋅h2
where h2 is the distance from the center of mass to point P.
Step 5: Set the Torques Equal
Setting the torques equal gives us:
mg⋅r=ma⋅h2
Step 6: Substitute for Acceleration
Substituting a=2bt into the torque equation:
mg⋅r=m(2bt)⋅h2
Step 7: Simplify the Equation
Cancel m from both sides:
gr=2bt⋅h2
This simplifies to:
gr=bht
Step 8: Solve for Time t
Rearranging the equation to solve for t:
t=grbh
Final Answer
The time when the cylinder is about to topple is:
t=grbh
The cylinder is on a conveyor belt that moves horizontally with a velocity given by the equation:
v=a+bt2
where a and b are constants, and t is time.
To find the acceleration of the cylinder, we differentiate the velocity with respect to time:
a=dvdt=ddt(a+bt2)=2bt
Thus, the acceleration a of the cylinder is:
a=2bt
When the cylinder is about to topple, we need to consider the forces acting on it:
- The weight of the cylinder mg acts downward at its center of mass.
- The normal force N acts upward at the base of the cylinder.
- A pseudo force Fpseudo=ma acts horizontally in the opposite direction of the acceleration of the belt.
For the cylinder to be in equilibrium just before toppling, the torque about the point of contact (point P) must be balanced. The torque due to the weight of the cylinder and the torque due to the pseudo force must be equal.
τweight=mg⋅r
where r is the radius of the cylinder.
τpseudo=ma⋅h2
where h2 is the distance from the center of mass to point P.
Setting the torques equal gives us:
mg⋅r=ma⋅h2
Substituting a=2bt into the torque equation:
mg⋅r=m(2bt)⋅h2
Cancel m from both sides:
gr=2bt⋅h2
This simplifies to:
gr=bht
Rearranging the equation to solve for t:
t=grbh
The time when the cylinder is about to topple is:
t=grbh
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - comprehension127videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 707videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 687videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise53videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
A cylinder of mass m and radius R is kept on a rough surface after giving its centre a horizontal speed v0. Find the speed of the centre of the cylinder when it stops slipping.
View SolutionA uniform cylinder of height h and radius r is placed with its circular face on a rough inclined plane and the inclination of the plane to the horizontal is gradually increased. If μ is the coefficient of friction, then under what condition the cylinder will (a) slide before toppling (b) topple before sliding.
View Solution
Knowledge Check
- Question 1 - Select One
A solid cylinder of mass M and radius R rolls without slipping down an inclined plane making an angle 6 with the horizontal. Then its acceleration is.
A1/3 g sinθB2/3 g sinθC2/5 g sinθD2/7 g sinθ
A solid cylinder of mass M and radius R rolls from rest down a plane inclined at an angle θ to the horizontal. The velocity of the centre of mass of the cylinder after it has rolled down a distance d is :
View Solution
A solid sphere of mass m and radius R is gently placed on a conveyer belt moving with constant velocity v0. If coefficient of friction between belt and sphere is 2/7 the distance traveled by the centre of the sphere before it starts pure rolling isView SolutionA cylinder of mass M and radius R is to be raised on a horizontal step of height h=R3. Cylinder is pulled by a rope as shown in figure. Assuming no slipping, the minimum value of force F to raise the cylinder is
_PHY_E05_246_Q01.png) View Solution
View SolutionA cylinder of height H and diameter H/4 is kept on a frictional turntable as shown in Fig. The axis of the cylinder is perpendicular to the surface of the table and the distance of axis of the cylinder is 2H from the centre of the table. The angular speed of the turntable at which the cylinder will start toppling (assume that friction is sufficient to prevent slipping) is
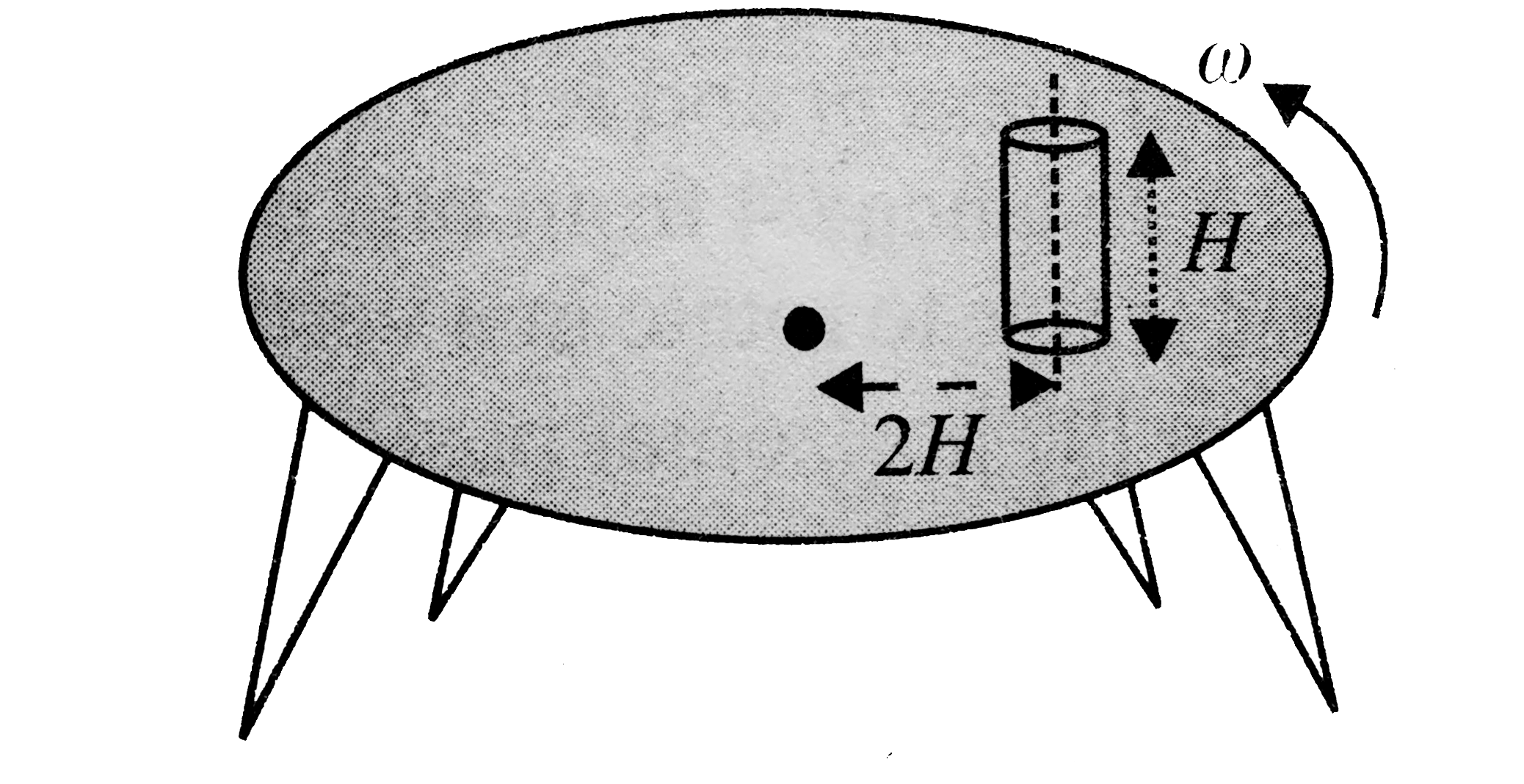 View Solution
View SolutionA homogeneous cylinder of mass Mand radius r is pulled on a horizontal plane by a horizontal force F acting through its centre of mass. Assuming rolling without slipping, find the angular acceleration of the cylinder,
View SolutionA homogeneous cylinder of mass Mand radius r is pulled on a horizontal plane by a horizontal force F acting through its centre of mass. Assuming rolling without slipping, find the angular acceleration of the cylinder,
View SolutionA cylinder of weight W and radius R is to be raised onto a horizontal step of height h as shown in Fig. A rope is wrapped around the cylinder and pulled horizontally with force F. Assuming the cylinder does not slip on the step, find the minimum force F necessary to raise the cylinder.
 View Solution
View Solution

