Figure shows a smooth track which consists of a straight inclined part of length l joining smoothly with the circular part. A particle of mass m is projected up the incline from its bottom. a.Find the minimum projected speed v0 for which the particle reaches the top of the track. b. Assuming that the projection speed is 2v0 and that the block does not lose contact with the track before reading its top, find the force acting on it when it reaches the top. c. Assuming that the projection speed is only slightly greater than v0 where will the block lose contact with the track?
The correct Answer is:(a) √2g[R(1−cosθ)+lsinθ]
(b) 6mg(1−cosθ+lRsinθ)
(c) The radius through the particle makes an angle cos−1(2/3)with the vertical
(a)12mv20=mglsinθ+mgR(1−cosθ)
v0=√2gR(1−cosθ)+2glsinθ

(b)C.O.E.
=12m(2v0)2=mglsinθ−mgR(1−cosθ)=12mv2
=2mv20−mglsinθ−mgR(1−cosθ)=12mv2
=4mgR(1−cosθ)+4mglsinθ−melsinθ−mgR(1−cosθ)=12mv2
=6mgR(1−cosθ)+6mglsinθ=mv2
N=6mg(1−cosθ)+6mglRsinθ
=6mg[(1−cosθ)+lRsinθ]

mgcosθ=mv2R
=12mv2=12mgRcosθ
=mgR(1−cosθ)=12mgRcosθ
cosθ=23tehta=cos−1(23).
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - comprehension
127 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 70
7 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 68
7 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
A particle of mass m is projected with a speed v0 at an angle of projection θ with horizontal. Find the torque of the weight of the particle about the point of projection after time v0sinθg
View Solution
A block is released from the top of the smooth inclined plane of height h. Find the speed of the block as it reaches the bottom of the plane.
View Solution
Knowledge Check
A body is projected up along an inclined plane from the bottom with speed is 2v.If it reaches the bottom of the plane with a velocity v,if θ is the angle of inclination with the horizontal and μ be the coefficient of friction.
A53tanθB35tanθC15tanθD25tanθA particle is projected on an inclined plane with a speed u as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
 .A2u2√3+13g.B4u2√3−19g.C2u2√5−18g.D2u2√3−13g
.A2u2√3+13g.B4u2√3−19g.C2u2√5−18g.D2u2√3−13gIn the figure shown, a particle is released from the position A on a smooth track. When the particle reaches at B, then normal reaction on it by the track. When the particle reaches at B, then normal reaction on it by the track is
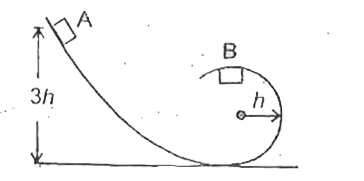 AmgB2mgC23mgDm2gh
AmgB2mgC23mgDm2gh
A particle is projected on an inclined plane with a speed u as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
 .
.
View SolutionIn the figure shown, a particle is released from the position A on a smooth track. When the particle reaches at B, then normal reaction on it by the track. When the particle reaches at B, then normal reaction on it by the track is

View SolutionA particle of mass m1 is projected to the right with speed v1 onto a smooth wedge of mass m2 which is simulateoulsy projected due the left with a speed v2. If the particle attains the highest point of the wedge, find h.

View SolutionA particle of mass m1 is projected to the right with speed v1 onto a smooth wedge of mass m2 which is simulateoulsy projected due the left with a speed v2. If the particle attains the highest point of the wedge, find h.

View SolutionA mass m is moving inside a vertical circular track of radius R. There is no friction. Find the minimum speed (vmin) at which m will round the circle without losing contact with the track. Suppose v=0.775vmin. The mass will move up to certain point P where it will lose contact with the track. Find the angular heightr of the track.
View Solution
