A concave spherical surface of radius of curvature 10cm separates two mediums X and Y of refractive indices 4/3 and 3/2 respectively. Centre of curvature of the surfaces lies in the medium X. An object is placed in medium X.
Image is always real
Image is real if the object distance is greater than 90cm
Image is always virtual
Image is virtual only If the object distance is less than 90cm.
The correct Answer is:C
To solve the problem, we will use the lens maker's formula and the information given about the concave spherical surface separating two media.
1. Identify the Given Values:
- Radius of curvature (R) = -10 cm (negative because the center of curvature is in medium X).
- Refractive index of medium X (n1) = 4/3.
- Refractive index of medium Y (n2) = 3/2.
2. Set Up the Lens Maker's Formula:
The lens maker's formula for a spherical surface is given by:
n2v−n1u=n2−n1R
where:
- n1 = refractive index of the medium where the object is placed (medium X).
- n2 = refractive index of the medium where the image is formed (medium Y).
- u = object distance (we will take it as -x, where x is positive).
- v = image distance.
3. Substitute the Values into the Formula:
Substituting the values into the formula:
3/2v−4/3−x=(3/2)−(4/3)−10
4. Simplify the Right Side:
First, calculate 32−43:
32=96,43=86⇒32−43=96−86=16
Now substitute this into the equation:
3/2v+4/3x=1/6−10
Simplifying the right side gives:
1/6−10=−160
5. Rearranging the Equation:
Now we have:
3/2v+4/3x=−160
6. Finding a Common Denominator:
Multiply through by 60vx to eliminate the denominators:
60x⋅32+60v⋅43=−vx
7. Solving for v:
Rearranging gives:
90x+80v=−vx
80v+vx=−90x
v(80+x)=−90x
v=−90x80+x
8. Analyzing the Sign of v:
Since x is positive, v will be negative, indicating that the image is virtual.
Conclusion:
The image formed is virtual.
- Radius of curvature (R) = -10 cm (negative because the center of curvature is in medium X).
- Refractive index of medium X (n1) = 4/3.
- Refractive index of medium Y (n2) = 3/2.
The lens maker's formula for a spherical surface is given by:
n2v−n1u=n2−n1R
where:
- n1 = refractive index of the medium where the object is placed (medium X).
- n2 = refractive index of the medium where the image is formed (medium Y).
- u = object distance (we will take it as -x, where x is positive).
- v = image distance.
Substituting the values into the formula:
3/2v−4/3−x=(3/2)−(4/3)−10
First, calculate 32−43:
32=96,43=86⇒32−43=96−86=16
Now substitute this into the equation:
3/2v+4/3x=1/6−10
Simplifying the right side gives:
1/6−10=−160
Now we have:
3/2v+4/3x=−160
Multiply through by 60vx to eliminate the denominators:
60x⋅32+60v⋅43=−vx
Rearranging gives:
90x+80v=−vx
80v+vx=−90x
v(80+x)=−90x
v=−90x80+x
Since x is positive, v will be negative, indicating that the image is virtual.
The image formed is virtual.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.10
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.11
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.8
Explore 9 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 19 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCE ENGLISHChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
A concave spherical surface of radius of curvature 100 cm separates two media of refractive indices 1.50 and 43. An object is kept in the first medium at a distance of 30 cm from the surface. Calculate the position of the image.
View SolutionA spherical surface of radius 30 cm separates two transparent media A and B with refractive indices 1'33 and 1.48 respectively. The medium A is on the convex side of the surface. Where should a point object be placed in medium A so that the paraxial rays become parallel after refraction at the surface ?
View Solution
Knowledge Check
A convex refracting surface of radius of curvature 20cm separates two media of refractive indices 4/3and1.60. An object is placed in the first medium (μ=4/3) at a distance of 200cm from the refracting surface. Calculate the position of image formed.
A120cmB240cmC100cmD60cm
A convex surface of radius of curvature 40 cm separate two media of refractive indices 43 and 1.50. An object is kept in the first medium at a distance of 20 cm from the surface. Calculate the position of the image.
View SolutionA spherical convex surface separates object and image space of refractive index 1.0and43. If radius of curvature of the surface is 10cm, find its power.
View SolutionA spherical convex surface separates object and image space of refractive index 1.0and43. If radius of curvature of the surface is 10cm, find its power.
View SolutionA concave spherical refractive surface with radius R separates a medium of refractive index 5/2 from air. As an object is approaching the surface from far away from the surface along the central axis, its image
View SolutionA spherical surface of radius R ssparates two media of refractive indices μ1 and μ1 as shown in figure., Where should an object be placed in medium 1 so that a real image is formed in medium 2 at the same distance?
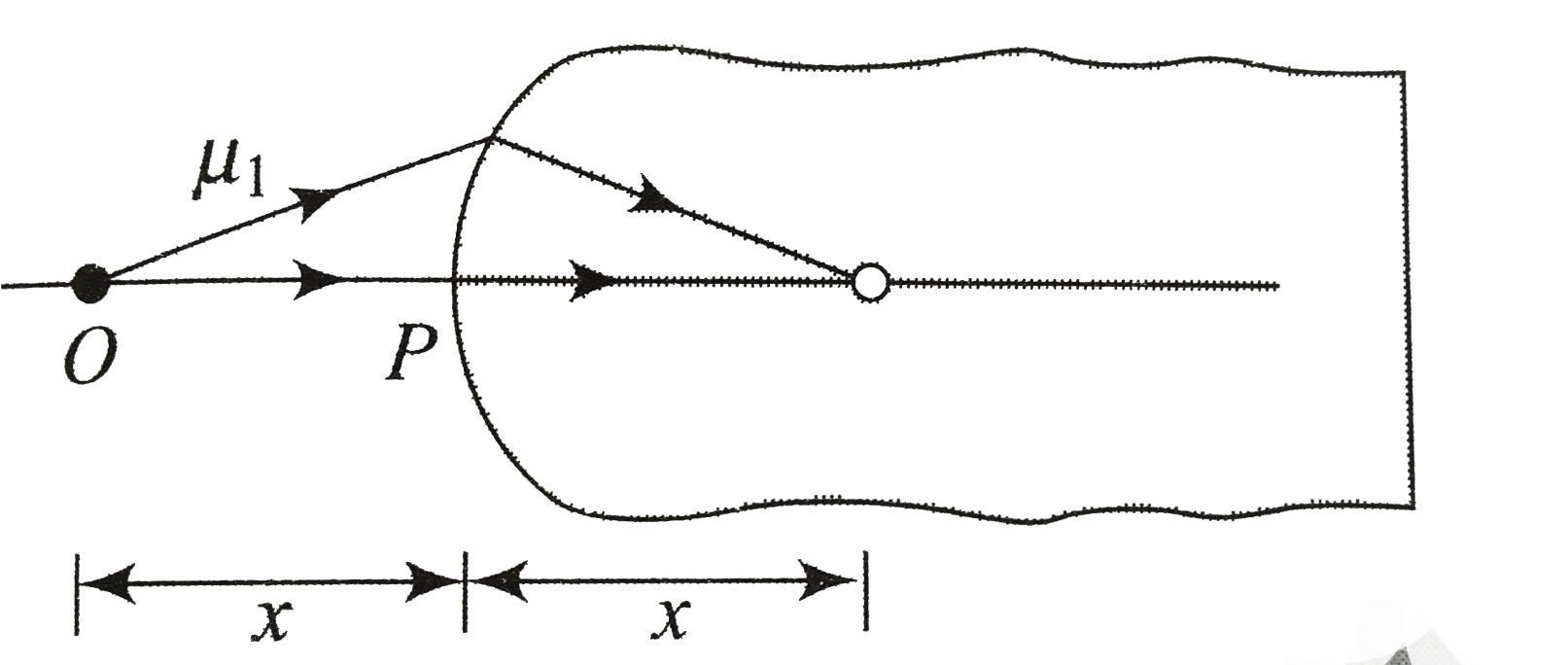
View SolutionA convex spherical refracting surface with radius R separates a medium having refractive index 5/2 from air. As an object is moved towards the surface from far away from the surface along the principle axis, its image
View SolutionFigure below shows a parallel beam of monochromatic light incident on a convex spherical surface, radius of curvature R = 30 cm, which separates glass (refractive index - 1 6) from air. Find the position of the image formed due to refraction of light at this single spherical surface.

View Solution
