Two graphs of the same projectile motion (in the xy-plane) projected from origin are shown. X-axis is along horizontal direction and y-axis is vertically upwards. Take g=10ms−2.
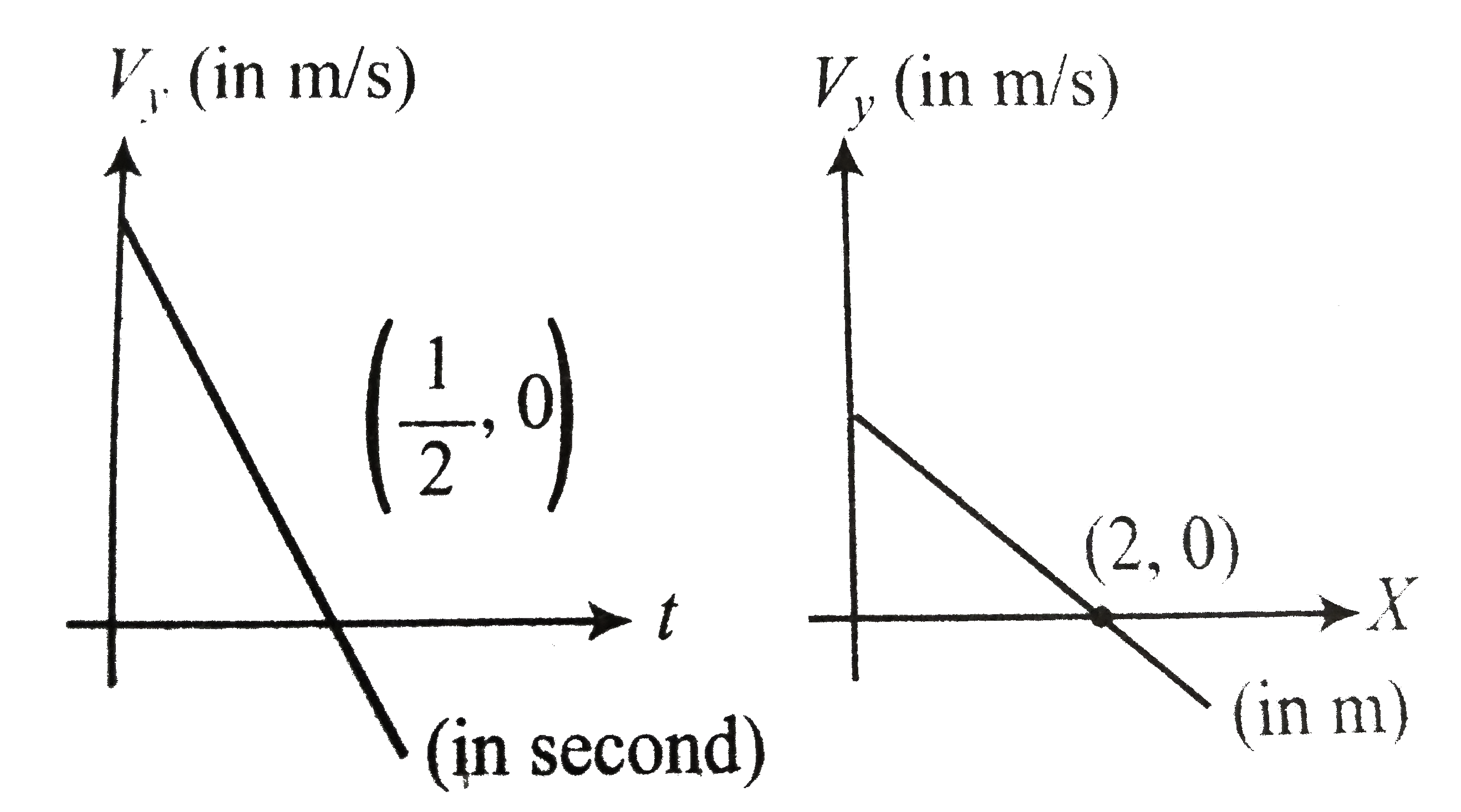
Projection angle with the horizontal is :
Y compenent of initial velocity is 5 m/s
X component of initial velocity is 4 m/s
Time to reach maximum height is 0.5 sec
All the above are correct
The correct Answer is:D
From graph (A) : Vy=0 at t=12sec
i.e., time taken to reach maximum height H is
t=uyg=12⇒uy=5m/s
from graph (B) : vy=0 at x=2m
i.e., when the particle is at maximum height, its displacement along horizontal x=2m
x=ux×t⇒2=ux×12
⇒ux=4m/s
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.18
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.19
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.16
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
Two graphs of the same projectile motion (in the xy-plane) projected from origin are shown. X-axis is along horizontal direction and y-axis is vertically upwards. Take g=10ms−2.
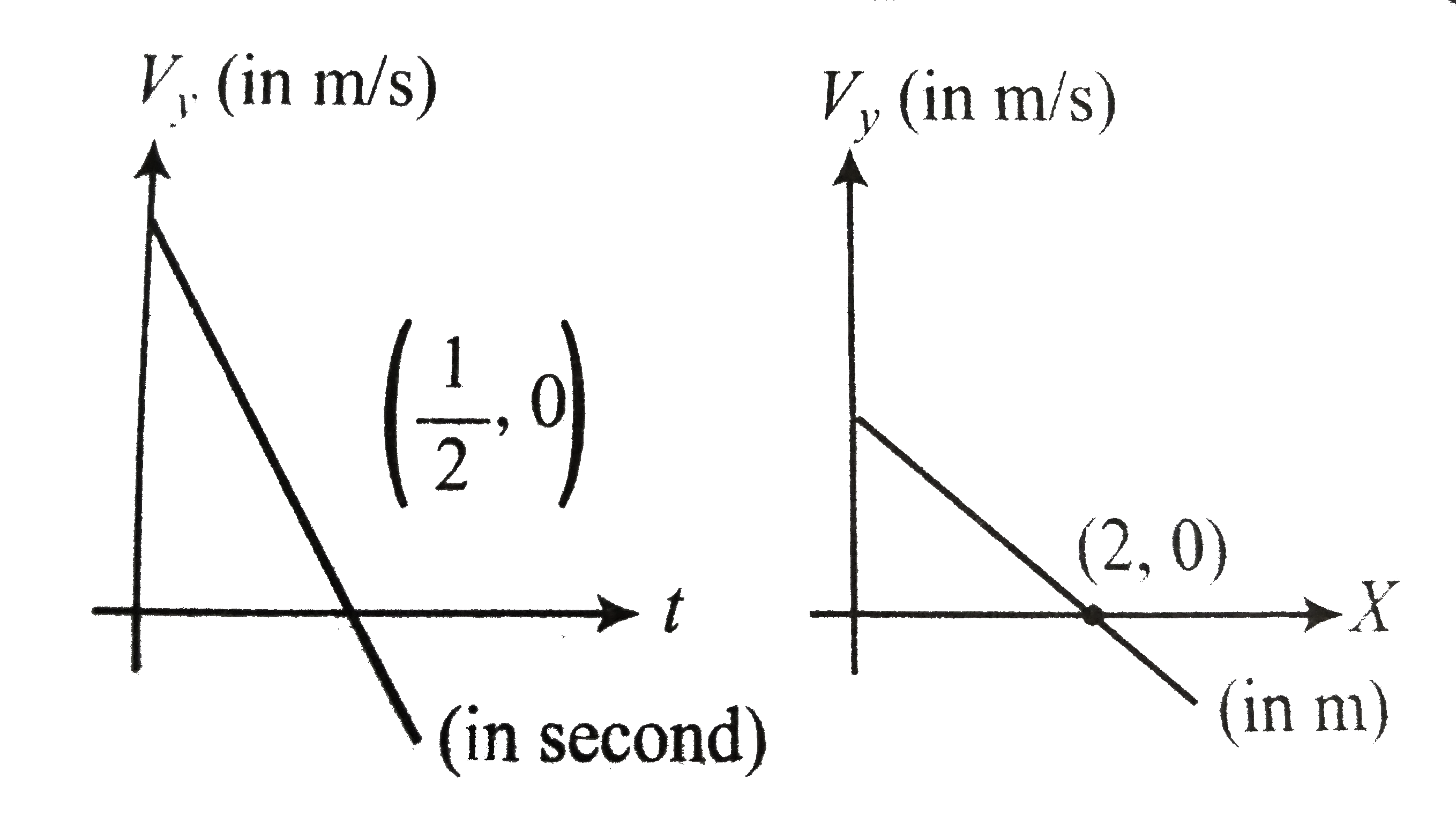 ,
,
The projection speed is :
View SolutionTwo graphs of the same projectile motion (in the xy-plane) projected from origin are shown. X-axis is along horizontal direction and y-axis is vertically upwards. Take g=10ms−2.
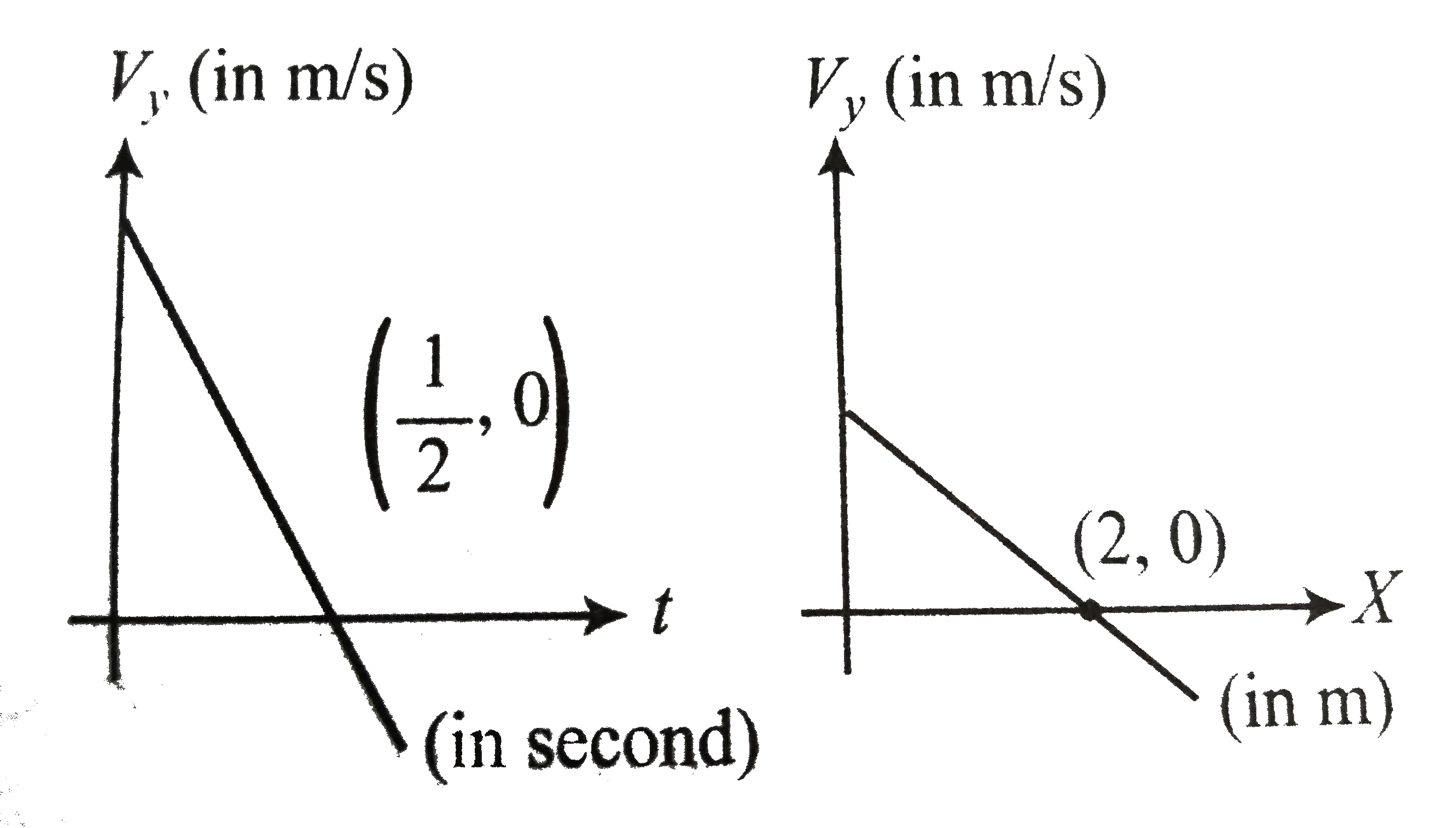 ,
,
Maximum height attained from the point of projection is
View Solution
A particle is projected from the horizontal x-z plane, in vertical x-y plane where x-axis is horizontal and positive y-axis vertically upwards. The graph of y coordinate of the particle v/s time is as shown . The range of the particle is √3. Then the speed of the projected particle is:
View SolutionA particle is projected from gound At a height of 0.4 m from the ground, the velocity of a projective in vector form is →v=(6ˆi+2ˆj)m/s (the x-axis is horizontal and y-axis is vertically upwards). The angle of projection is (g=10m/s2)
View SolutionAt a height of 15 m from ground velocity of a projectile is v=(10ˆi+10ˆj). Here ˆj is vertically upwards and ˆi is along horizontal direction then (g = 10 ms−1)
View SolutionFor shown situation draw a graph showing acceleration of A and B on y-axis and time on x-axis (g=10ms−2)

View SolutionPressure gradient in the horizontal direction in a static fluid is represented by (z-direction is vertically upwards, and x-axis is along horizontal, d is density of fluid):
View SolutionA particle is projected from ground at some angle with horizontal (Assuming point of projection to the origin and the horizontal and vertical directions to be the x and y axis) the particle passes through the points (3, 4) m and (4, 3) m during its motion then the range of the particle would be : (g=10m/s2)
View SolutionA bullet is fired from horizontal ground at some angle passes through the point (3R/4 ,R/4), where R is the range of the bullet. Assume point of the fire to be origin and the bullet moves in x-y plane with x-axis horizontal and y-axis vertically upwards. Then angle of projection is
View SolutionA particle is projected in the x-y plane with y-axis along vertical. Two second after projection the velocity of the particle makers an angle 45∘ with the X-axis. Four second after projection. It moves horizontally. Find velocity of projection.
View Solution
