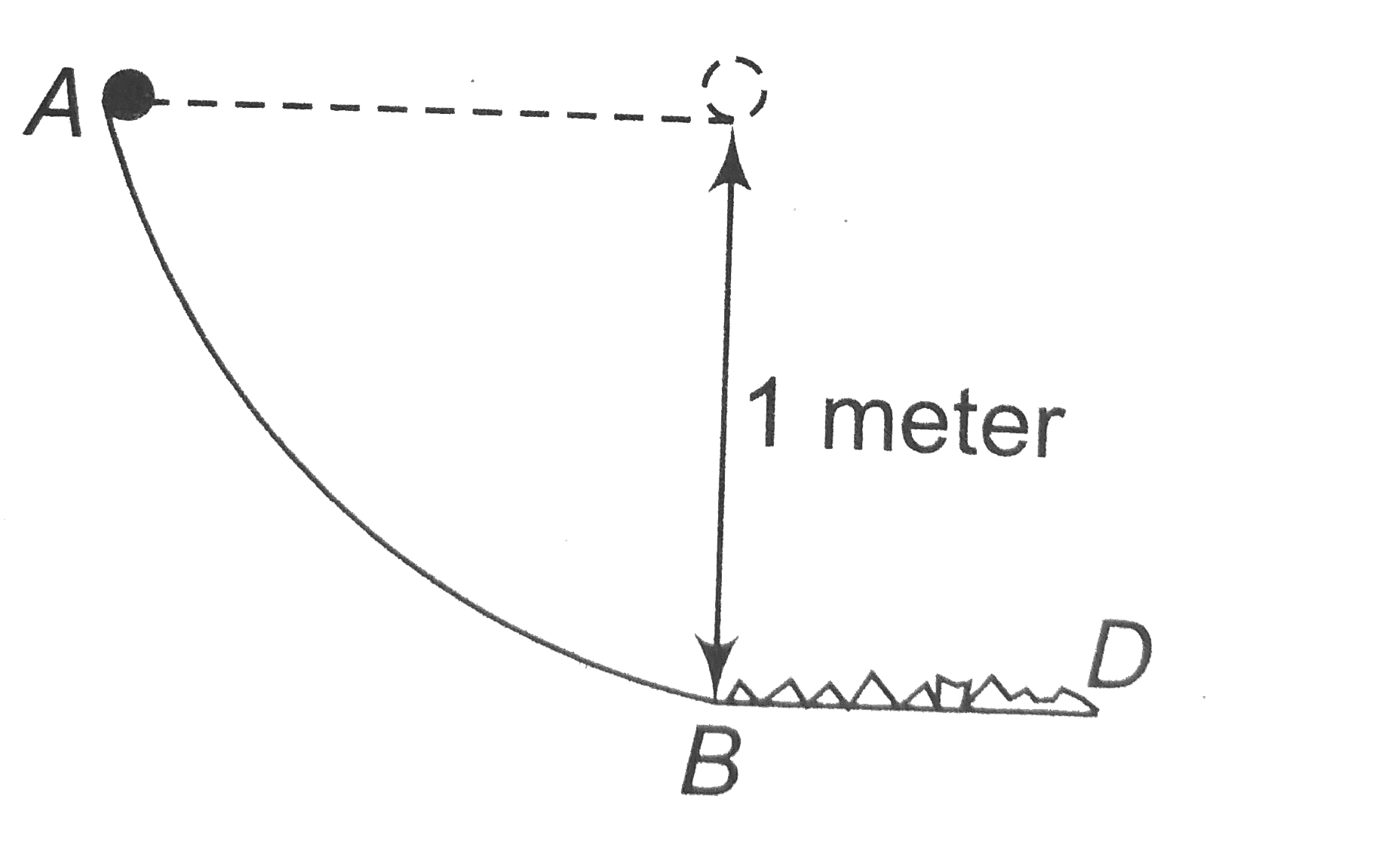
In the track shown in figure section AB is a quadrant of a circle of 1 meter radius. A block is released at A and slides without friction until it reaches B. After B it moves on a rough horizontal floor and comes to rest at distance 3 meters from B. What is the coefficient of friction between floor and body?
1/3
2/3
1/4
3/8
The correct Answer is:A
mg1=12mu2⇒u2=2g...(1)
v2=u2+2as⇒0=2g−2a(3)
⇒a=g3⇒μkg=a
∴μkg=g3
∴uk=13
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.20
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.21
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.18
Explore 9 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 19 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCE ENGLISHChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
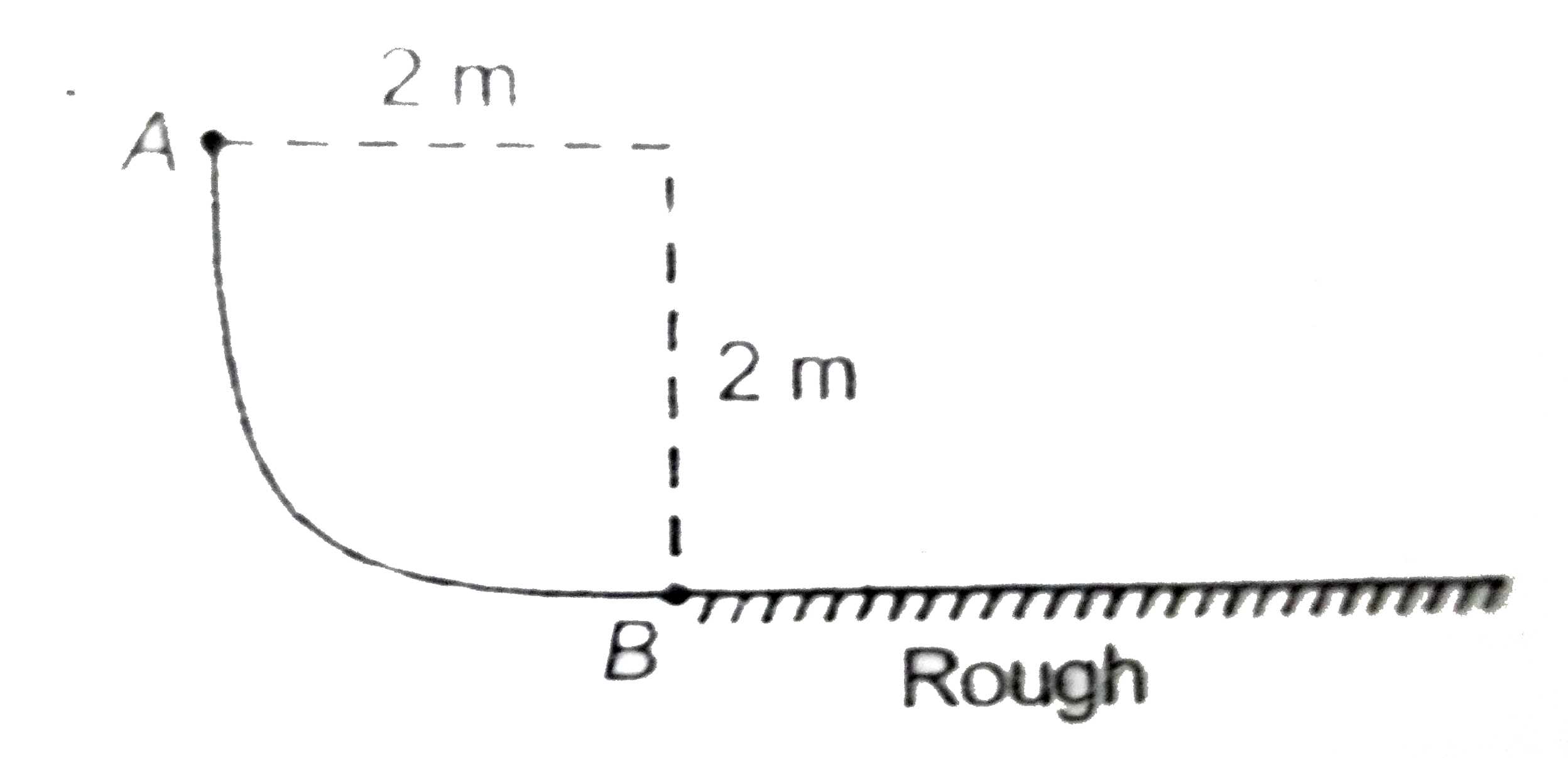
A block is released at A and slides on smooth surface in shape of quarter circel. The horizontal part is rough if the block comes to rest 1.0 m away from B, then what is the coefficient of kinetic friction?
View SolutionThe three blocks in figure are released from rest and accelerate at the rate of 2 ms2. If M = 5 kg , what is the coefficient of friction between the surface and the block B ?

View Solution
Knowledge Check
A block slides with a velocity of 10 m/sec. on a rough horizontal surface. It comes to rest after covering of 50 m. If g is 10 m/sec2, then the coefficient of dynamic friction between the block and surface is
A1B10C2D0.1
A block of mass m is released on the top of a smooth inclined plane of length x and inclination θ as shown in figure. Horizontal surface is rough. If block comes to rest after moving a distabce d on the horizontal surface, then coefficient of friction between block and surface is :-
View SolutionA body is moving along a rough horizontal surface with an initial velocity 6m/s m If the body comes to rest after travelling 9 m , then the coefficient of sliding friction will be
View SolutionStarting from rest a wooden block moves with a velocity of 25ms−1 along a rough ground and comes to rest. Calculate the distance travelled by the wooden block on the rough surface of coefficient of friction 0.25.
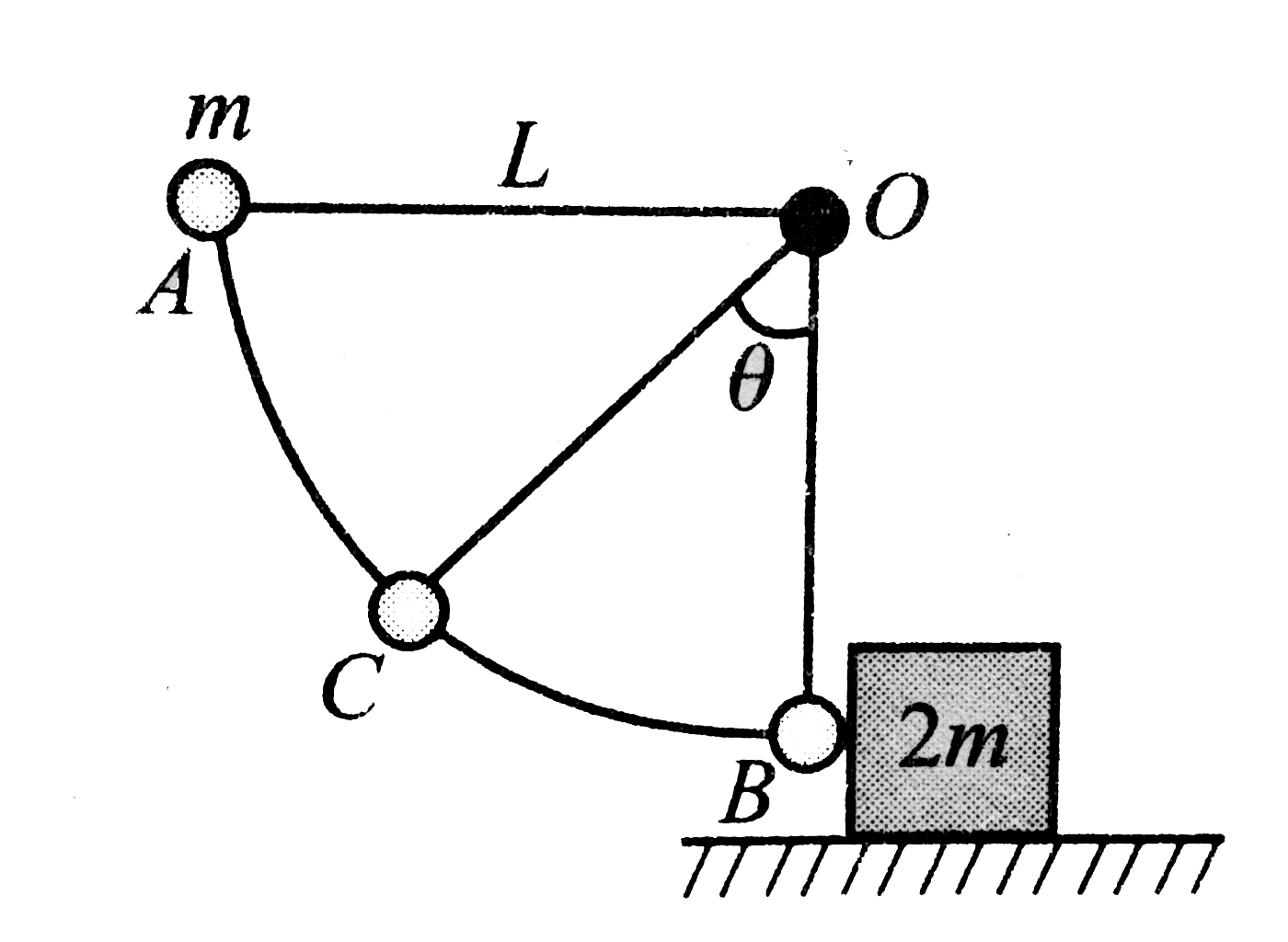
View SolutionA ball of mass m is attached to a cord of length L, pivoted at point O, as shown in Fig. The ball is released from rest at point A, swings down and makes an inelastic collision with a block of mass 2m kept on a rough horizontal floor. The coefficient of restitution of collision is e=2/3 and coefficient of friction between block and surface is After collision, the ball comes momentarily to rest at C when cord makes an angle of θ with the vertical and block moves a distance of 3L/2 on rough horizontal floor before stopping. The values of μ and θ are, respectively,
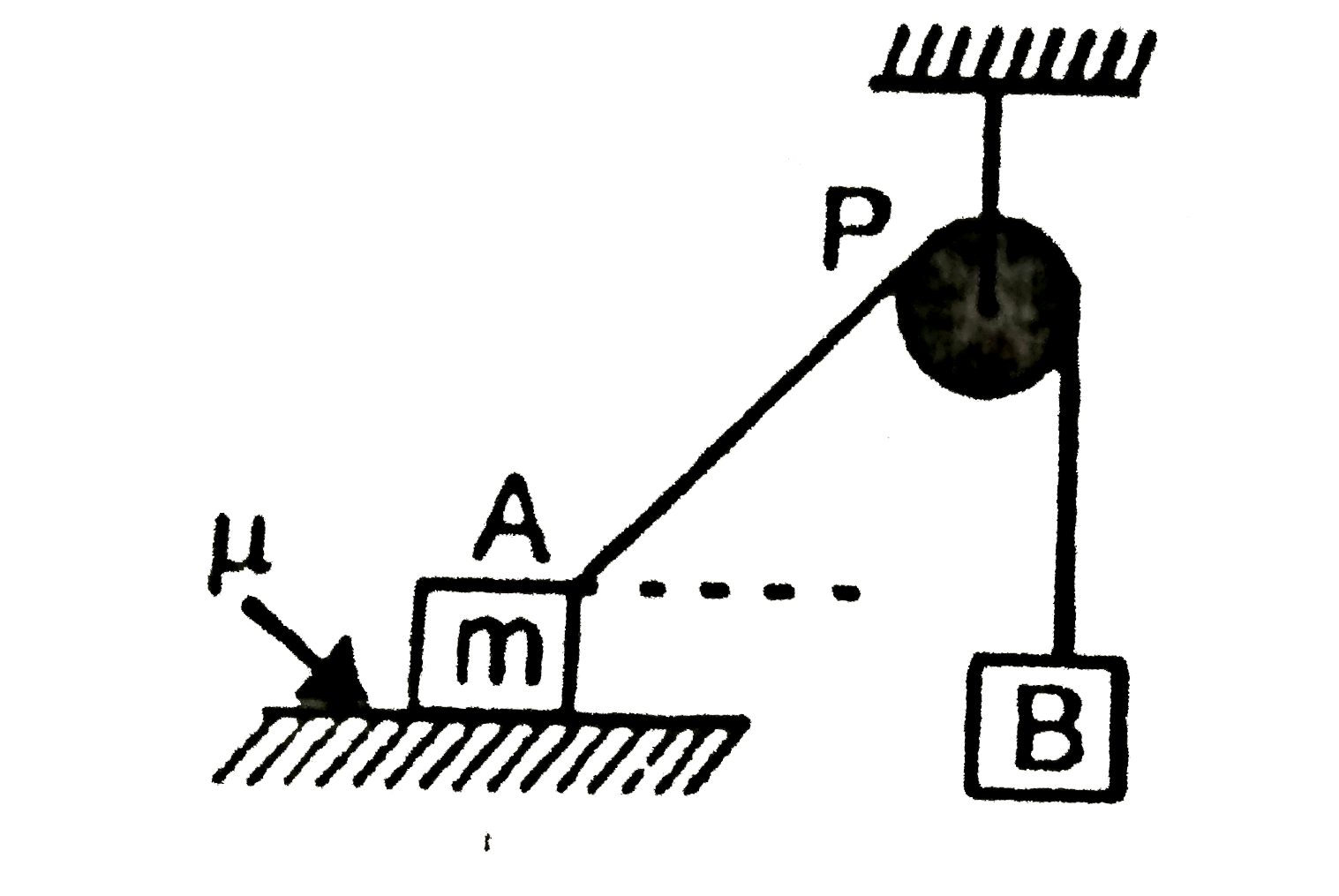
View SolutionIn figure shown minimum mass of block B( at a particular angle between horizontal and string AP) to just slide the block A on rough horizontal surface is m2 as shown in figure. If μ is the coefficient of friction between block A and ground then pμ2 will be :
View Solution
Two blocks A (1 kg) and B (2 kg) are connected by a string passing over a smooth pulley as shown in the figure. B rests on rough horizontal surface and A rest on B. The coefficient of friction between A and B is the same as that between B and the horizontal surface. The minimum horizontal force F required to move A to the left is 25 N. The coefficient of friction is:
View Solution
A block B is placed over a cart which in turn lies over a smooth horizontal floor. Block A and Block C are connected to block B with light inextensible strings passing over light frictionless pulleys fixed to the cart as shown. Initially the blocks and the cart are at rest. All the three blocks have mass m and the cart has mass M(M=3m). Now a constant horizontal force of magnitude F is applied to block A towards right.
Q. Let the coefficient of friction between block B and cart is μ(μ>0) and friction is absent everywhere else. Then the maximum value of force F applied to block A such that there is no relative acceleration between block B and cart is
View Solution