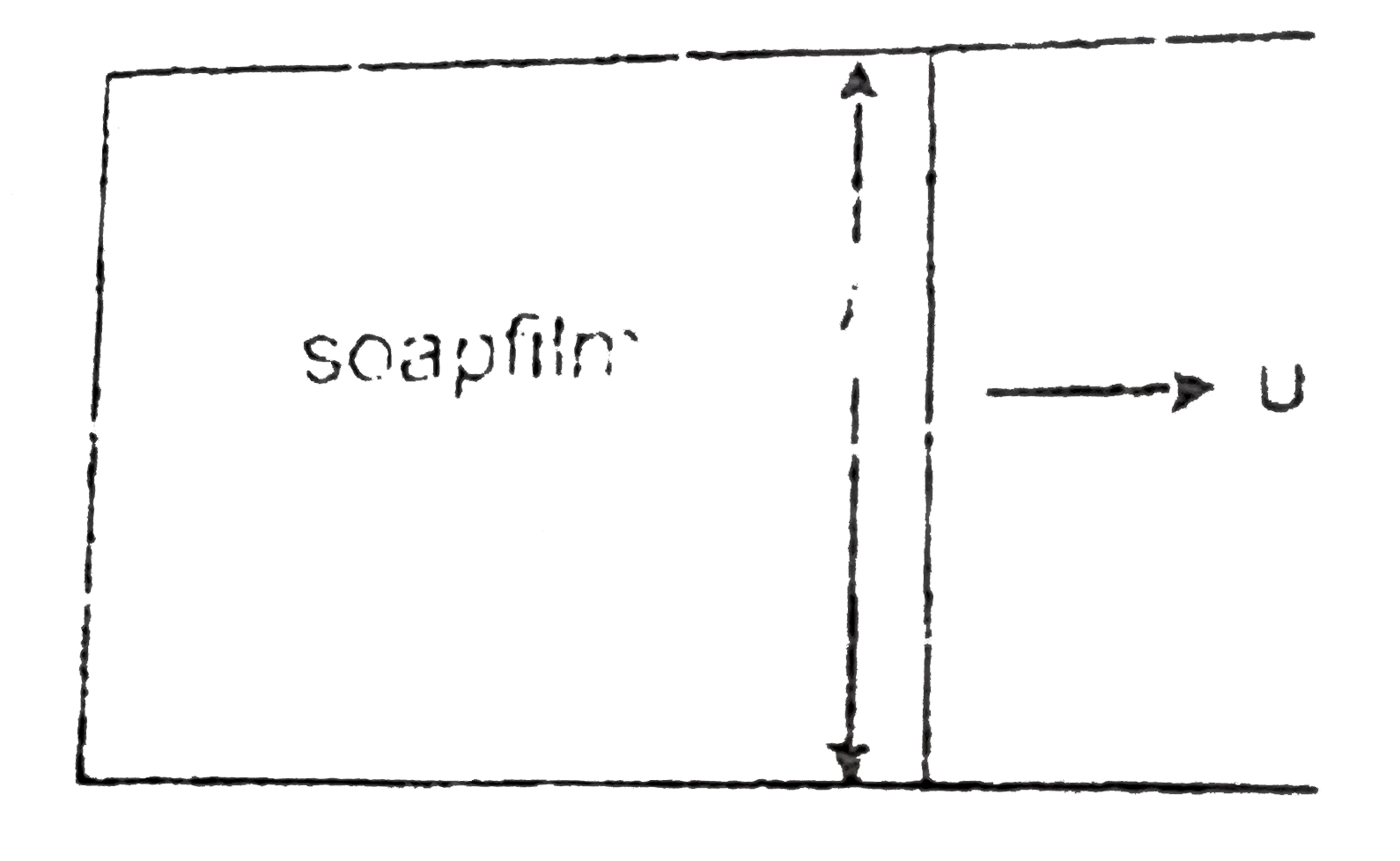
A soap film is created in a small wire frame as shown in the figure. The sliding wire of mass m is given a velocity u to the right and assume that u is small enough so that film does not break. Plane of the film is horizontal and surface tension is T, then time to region the original position of wire is equal to :
umTl
Tlum
mu2lT
It will never regain original position
The correct Answer is:A
a=2Tlm
v=I+at⇒0=u−at
t=ua=um2Tl
Total time T=2t=umTl
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.3620videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.379videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.349videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)19videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
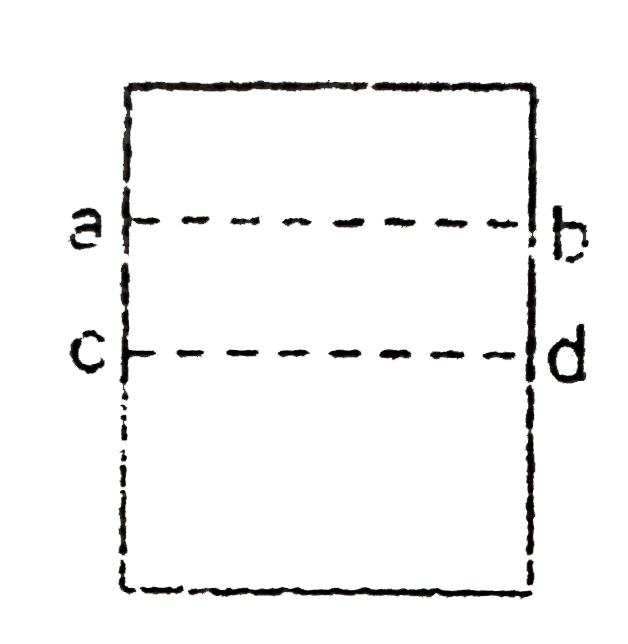
A soap film in stretched over a reclangular vertical wire frame as shown in the figure, what forces hold section abod in equilibrium ?
 View Solution
View SolutionA wire of mass 1g is kept horizontally on the surface of water. The length of the wire that does not break the surface film is (surface tension of water is 70dy≠cm−1)
View SolutionA wire of mass 5 gm is kept horizontally on the surface of water. What ist he minimum length of the wire so that it does not break the surface film.Surface tension =72×10−3N/m
View SolutionA small block is resting on an inclined plane (co-efficient of friction μ>tanθ) as shown in the figure. The inclined plane is given a constant horizontal acceleration 'a' towards right.
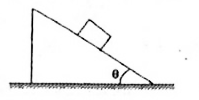
(a) Find the range of 'a' such that the bock does not slide on the plane.
(b) Find the value of 'a' such that the firction force between the block and the plane is zero.View SolutionA wire ring of diameter 0.03m is dipped in a liquid and pulled out gently. If a force of 0.1N is required to break the film, then what is the surface tension of the liquid?
View SolutionA horizontal wire is free to slide on the verticle rails of a conducting frame as shown in figure. The wire has a mass m and length l and the resistance of the circuit is R. If a uniform magnetic field B is directed perpendicular to the frame, the terminal speed of the wire as it falls under the force of gravity is
 View Solution
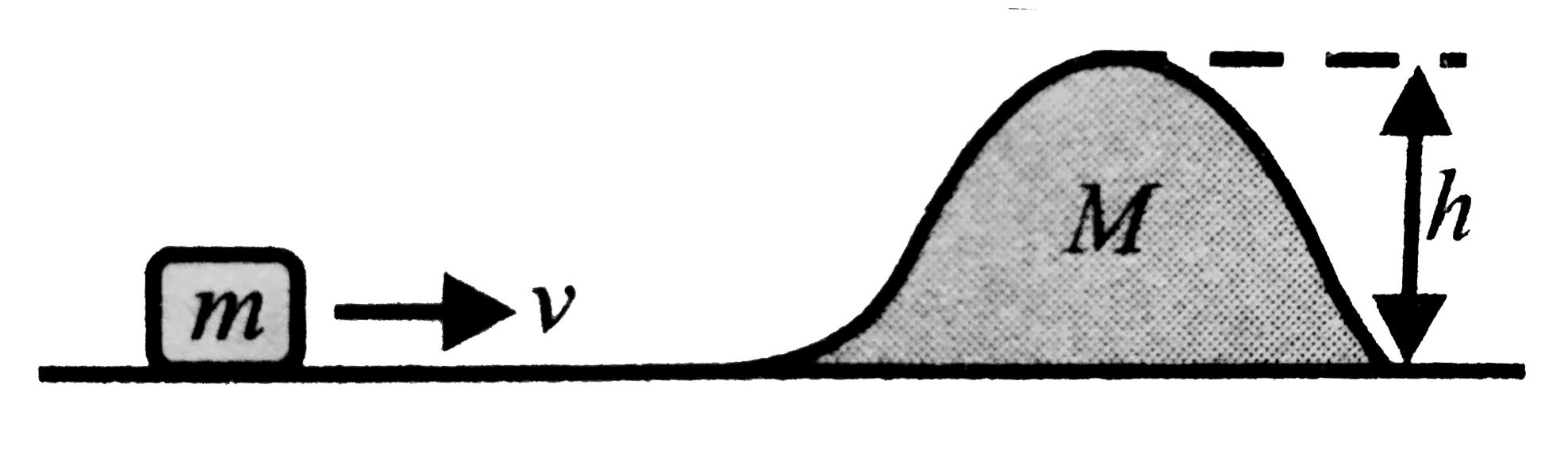
View SolutionFor the system shown in the figure, a small block of mass m and smooth irregular shaped block of mass M, both free to move are placed on a smooth horizontal plane. The minimum velocity v imparted to block so that it will overcome the highest point of M is
 View Solution
View SolutionA U-shaped wire is dipped in a soap solution, and removed. A thin soap film formed between the wire and a light slider supports a weight of 1.5×10−2N (which includes the small weigh of the slider). The length of the slider is 30cm. What is the surface tension of the film?
View SolutionA thin and light thread of sufficient length L is attached to a wire frame. The frame (along with the thread) is dipped into soap solution. When the frame is taken out of the solution, the thread takes the form of a semicircle with a soap film extending between the frame and the thread as shown in the figure (a). Now the thread is deformed into two semicircles by applying a force of F at the middle of the thread, as a result the film gets strectched as shown in the figure. (b). Calculate the surface tension of the soap solution.
 View Solution
View SolutionA small spehre of mass m is connected by a stirng to a nail at O and moves in a circle of radius r on the smooth plane inclined at an angle θ with the horizontal. If the sphere has a velocity u at the top position A. Mark the correct options.
1)the tension in the string as the sphere passes the 90∘ position B is equal to m( u^2/l − 2gsinθ )
2)the tension in the string at the bottom most position C is equal to
m( u^2/l + 5gsinθ )
3)the tension in the string as the sphere passes the 90∘ position B is equal to m( u^2/l + 2gsinθ )
4)the tension in the string at the bottom most position C is equal to
m( u^2/l − 5gsinθ )
 View Solution
View Solution

