Two solids A and B floats in water. It is observed that A floats with half of its volume immersed and B Floats with 2/3 of its volume immersed. The ratio of densities of A and B is
4:3
2:3
3:4
1:3
The correct Answer is:C
To find the ratio of the densities of solids A and B, we can use the principle of buoyancy, which states that the buoyant force acting on a floating object is equal to the weight of the fluid displaced by the object.
1. Understanding the Problem:
- Solid A floats with half of its volume immersed in water.
- Solid B floats with two-thirds of its volume immersed in water.
- We need to find the ratio of the densities of solids A and B.
2. Setting Up the Equations:
- Let the density of solid A be ρA and the density of solid B be ρB.
- The volume of solid A is V, so the volume submerged is 12V.
- The volume of solid B is also V, so the volume submerged is 23V.
3. Applying the Buoyancy Principle:
- The weight of solid A is given by:
WA=ρA⋅V⋅g
- The buoyant force acting on solid A is:
FbA=ρwater⋅(12V)⋅g
- Setting the weight equal to the buoyant force for solid A:
ρA⋅V⋅g=ρwater⋅(12V)⋅g
- Simplifying this gives:
ρA=12ρwater
4. Repeating for Solid B:
- The weight of solid B is given by:
WB=ρB⋅V⋅g
- The buoyant force acting on solid B is:
FbB=ρwater⋅(23V)⋅g
- Setting the weight equal to the buoyant force for solid B:
ρB⋅V⋅g=ρwater⋅(23V)⋅g
- Simplifying this gives:
ρB=23ρwater
5. Finding the Ratio of Densities:
- Now we can find the ratio of the densities ρAρB:
ρAρB=12ρwater23ρwater=12⋅32=34
Final Answer:
The ratio of the densities of solids A and B is:
ρAρB=34
- Solid A floats with half of its volume immersed in water.
- Solid B floats with two-thirds of its volume immersed in water.
- We need to find the ratio of the densities of solids A and B.
- Let the density of solid A be ρA and the density of solid B be ρB.
- The volume of solid A is V, so the volume submerged is 12V.
- The volume of solid B is also V, so the volume submerged is 23V.
- The weight of solid A is given by:
WA=ρA⋅V⋅g
- The buoyant force acting on solid A is:
FbA=ρwater⋅(12V)⋅g
- Setting the weight equal to the buoyant force for solid A:
ρA⋅V⋅g=ρwater⋅(12V)⋅g
- Simplifying this gives:
ρA=12ρwater
- The weight of solid B is given by:
WB=ρB⋅V⋅g
- The buoyant force acting on solid B is:
FbB=ρwater⋅(23V)⋅g
- Setting the weight equal to the buoyant force for solid B:
ρB⋅V⋅g=ρwater⋅(23V)⋅g
- Simplifying this gives:
ρB=23ρwater
- Now we can find the ratio of the densities ρAρB:
ρAρB=12ρwater23ρwater=12⋅32=34
The ratio of the densities of solids A and B is:
ρAρB=34
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.43
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.44
10 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.41
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
Two cubical blocks identical in dimensions float in water in such a way that 1st block floats with half part immersed in water and second block floats with 3/4 of its volume inside the water. The ratio of densities of blocks is
View SolutionA block of wood of volume 30cm3 floats it water with 20cm3 of its volume immersed.
Calculate the density.
View SolutionA block of wood floats in freshwater with two - third of its volume submerged . In oil , the block floats with one - fourth of its volume submerged. The density of oil is
View SolutionA body P floats in water with half its volume immersed. Another body Q floats in a liquid of density 34th of the density of water with two - third of the volume immersed. The ratio of density of P to that of Q is
View SolutionA body floats in water with 40% of its volume outside water. When the same body floats in an oil. 60% of its volume remians outside oil. The relative density of oil is
View SolutionA piece of wood floats in water with two-thirds of its volume submerged in water. In a certain oil it has 0.95 of its volume submerged. What is the density of wood and the oll?
View SolutionA solid body floating in water has 15th of its volume immersed in it. What fraction of its volume will be immersed, if it floats in a liquid of specific gravity 1.2 ?
View SolutionA body floats in water with its one-third volume above the surface. The same body floats in a liquid with one-third volume immersed. The density of the liquid is
View SolutionA block of density ρ floats in a liquid with its one third volume immersed. The density of the liquid is
View Solution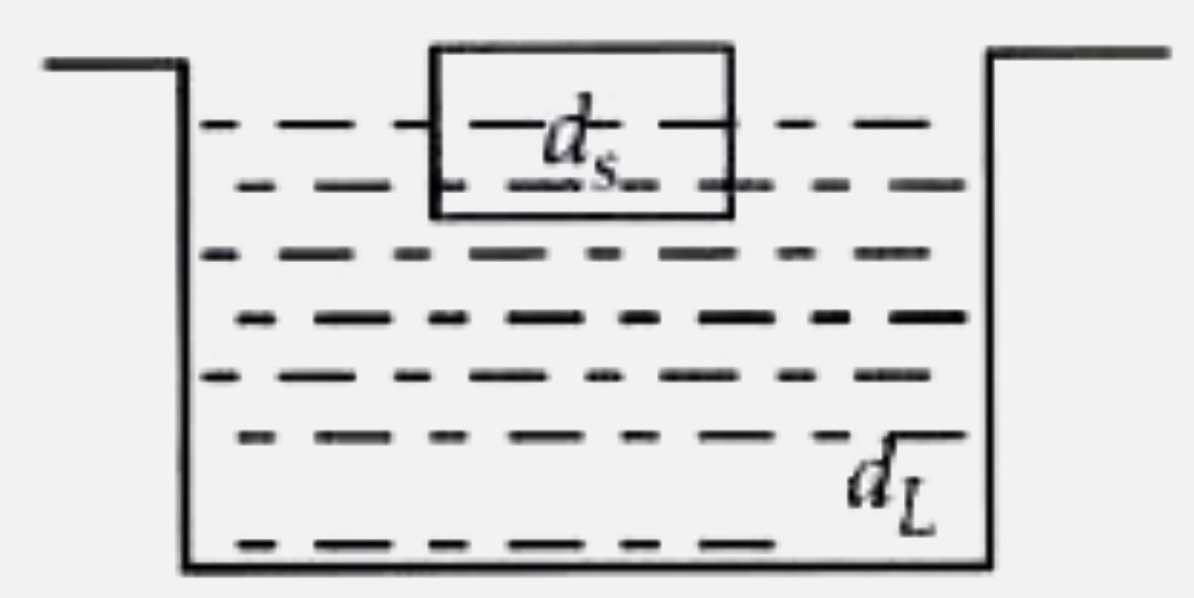
The figure above shows a solid of density dS floating in a liquid of density dL.
The same solid floats in water with 3th5 of its volume immersed in it. Calculate the density of the solid. (density of water = 1 g cm−3 )
View Solution
