A transparent solid cube of side 'a' has refractive index 3/2. A point source of light is embedded in it at its centre. Find the minimum area of the surface of the cube which must be painted black so that the source is not visible from outside.
The correct Answer is:6πa25
To solve the problem of determining the minimum area of the surface of a transparent solid cube that must be painted black so that a point source of light embedded at its center is not visible from outside, we can follow these steps:
1. Understanding the Geometry:
- The cube has a side length of 'a'.
- The point source of light is located at the center of the cube.
2. Critical Angle Calculation:
- The refractive index of the cube (denser medium) is given as μd=32.
- The refractive index of air (rarer medium) is μr=1.
- The critical angle θc can be calculated using Snell's law:
sinθc=μrμd=132=23
3. Finding the Radius of the Circle:
- The radius R of the circular area from which the light source is visible can be determined using the geometry of the problem. The distance from the center of the cube to the face is a2.
- Using the relationship involving the critical angle:
R=(a2)tanθc
- To find tanθc, we can use the identity:
tanθc=sinθc√1−sin2θc=23√1−(23)2=23√59=23⋅3√5=2√55
- Therefore, substituting back:
R=(a2)⋅2√55=a√55
4. Calculating the Area to be Painted:
- Since the cube has 6 faces and the area of each circular region (where the source is visible) is given by:
Acircle=πR2=π(a√55)2=π⋅5a225=πa25
- The total area to be painted black on all 6 faces is:
Atotal=6⋅Acircle=6⋅πa25=6πa25
Final Answer:
The minimum area of the surface of the cube that must be painted black so that the source is not visible from outside is:
6πa25
- The cube has a side length of 'a'.
- The point source of light is located at the center of the cube.
- The refractive index of the cube (denser medium) is given as μd=32.
- The refractive index of air (rarer medium) is μr=1.
- The critical angle θc can be calculated using Snell's law:
sinθc=μrμd=132=23
- The radius R of the circular area from which the light source is visible can be determined using the geometry of the problem. The distance from the center of the cube to the face is a2.
- Using the relationship involving the critical angle:
R=(a2)tanθc
- To find tanθc, we can use the identity:
tanθc=sinθc√1−sin2θc=23√1−(23)2=23√59=23⋅3√5=2√55
- Therefore, substituting back:
R=(a2)⋅2√55=a√55
- Since the cube has 6 faces and the area of each circular region (where the source is visible) is given by:
Acircle=πR2=π(a√55)2=π⋅5a225=πa25
- The total area to be painted black on all 6 faces is:
Atotal=6⋅Acircle=6⋅πa25=6πa25
The minimum area of the surface of the cube that must be painted black so that the source is not visible from outside is:
6πa25
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.4520videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.4611videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.4320videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)19videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
A disc is placed on a surface of pond which has refractive index 35 . A source of light is placed 4 m below the surface of liquid. The minimum radius of disc will be so light is not coming out
View SolutionRefractive index of water is 5/3. A light source is placed in water at a depth of 4m. Then what must be the minimum radius of disc placed on water surface so that the light of source can be stopped?
View Solution
Knowledge Check
- Question 1 - Select One
A point source of light is placed at a depth of h below the surface of water of refractive index μ. A floating opaque disc is placed on the surface of water so that light from the source is not visible from the surface. The minimum diameter of the disc is
A2h(μ2−1)1/2B2h(μ2−1)1/2Ch2(μ2−1)1/2Dh(μ2−1)1/2
A disc is placed on the surface of pond filled with liquid of refractive index 53. A source of light is placed 4m below the surface of liquid. Calculate the minimum area of the disc so that light does not come out of liquid.
View SolutionA rectangulat block of refractive index μ is placed on a printed page lying on a horizontal surface as shown in Fig. , Find the minimum value of μ so that the letter L on the page is not visible from any of the vertical sides.
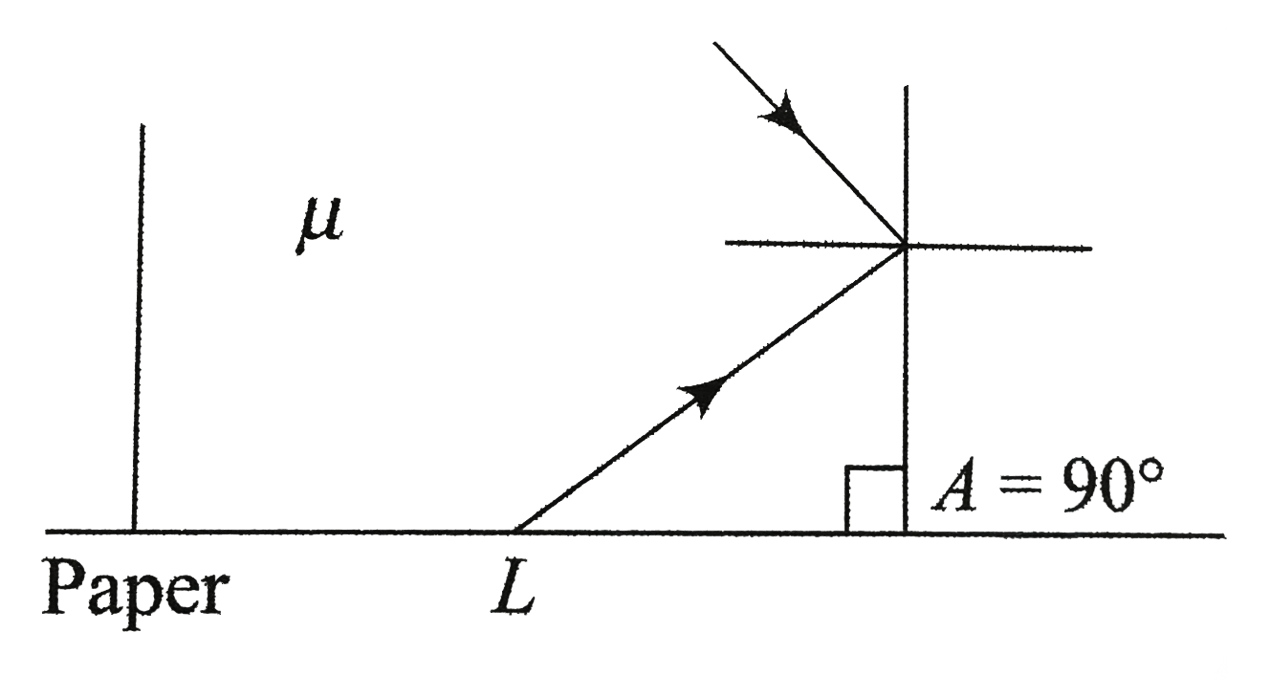 View Solution
View SolutionA slab of refractive index μ is placed in air and light is incident at maximum angle θ0 from vertical. Find minimum value of μ for which total internal reflection takes place at the vertical surface.
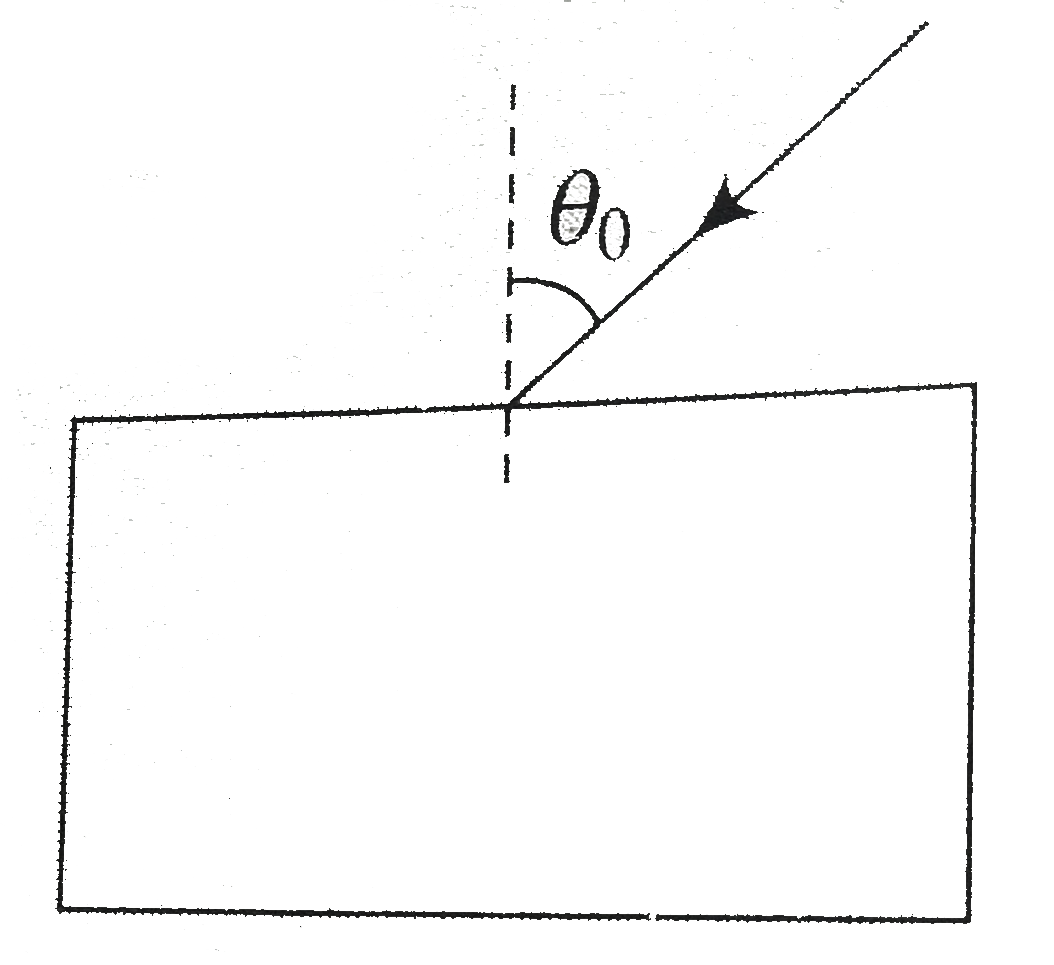 View Solution
View SolutionA parallel beam of light emerges from the opposite surface of the sphere when a point source of light lies at the surface of the sphere. The refractive index of the sphere is
View SolutionA point source is placed at a depth h below the surface of water (refractive index =μ). The medium above the surface area of water is air from water.
View SolutionA point source of light is placed 4 m below the surface of water of refractive index 53. The minimum diameter of a disc, which should be placed over the source, on the surface of water to cut off all light coming out of water is
View SolutionA transparent solid cylindrical rod has a refractive index of 2√3 .It is surrounded by air. A light ray is incident at the mid-point of one end of the rod as shown in the figure. The incident angle θ for which the light ray grazes along the wall of the rod is:
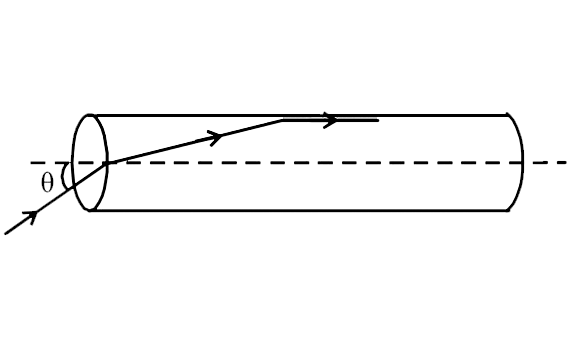 View Solution
View Solution

