A small sized mass m is attached by a massless string (of length L) to the top of a fixed frictionless solid cone whose axis is vertical. The half angle at the vertex of cone is theta. If the mass m moves around in a horizontal circle at speed v , what is the maximum value of v for which mass stay in contact with the comes? (g is acceleration due to gravity.)
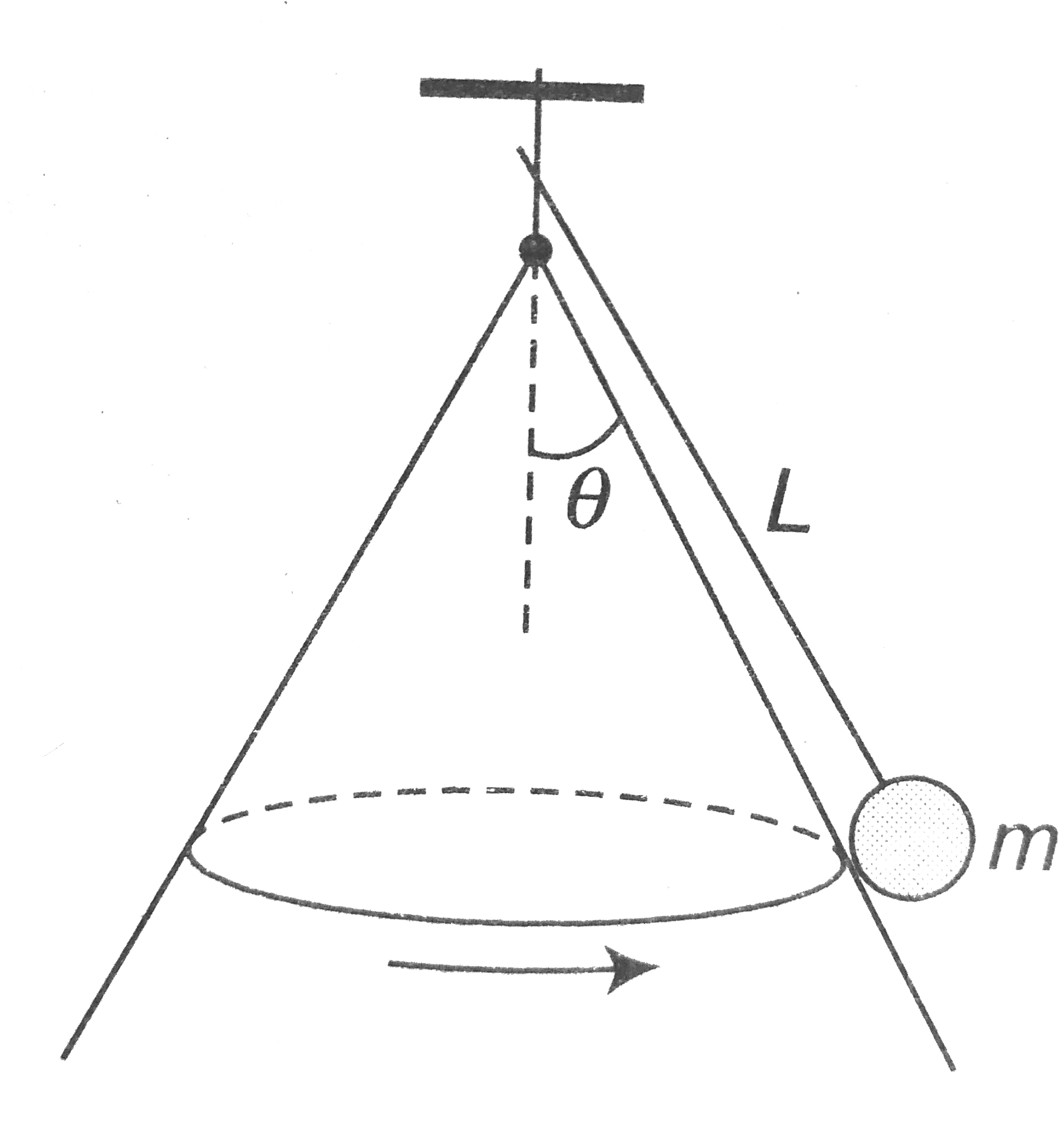
√gLcosθ
√gLsinθ
√gLsinθtanθ
√gLtanθ
The correct Answer is:C
At maximum velocity the mass will just loose contact with cone and will behave like free conical pendulum with time period :
T=2π√Lcosθg⇒ω=2πT√gLcosθ
Hence vmax=(Lsinθ)ω=√gLsinθtanθ.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.529videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.5320videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.509videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)19videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
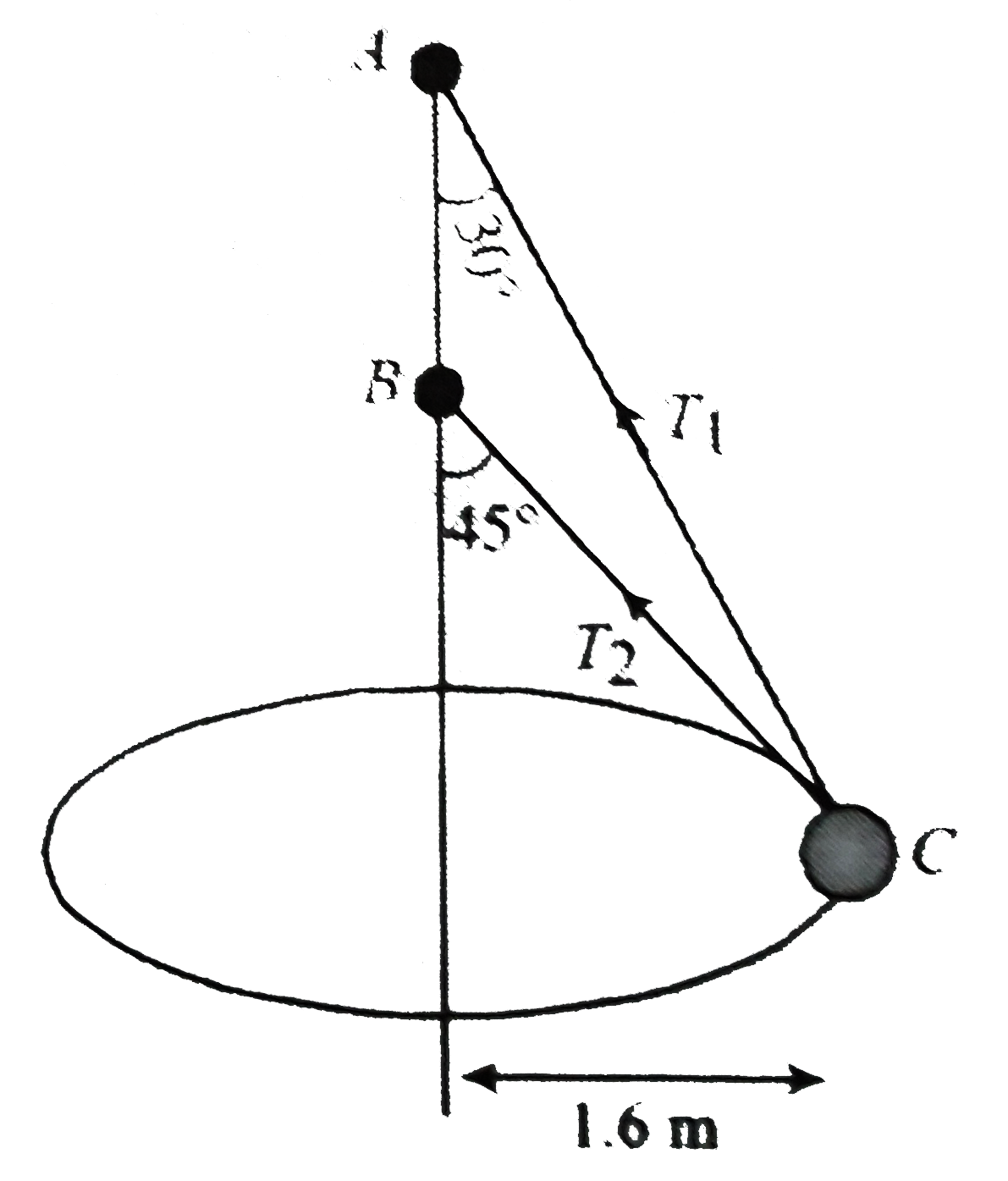
Two wires ACandBC are tied at C of small sphere of mass 5kg which revolves at a constant speed v in the horizontal circle of radius 1.6m Find the maximum value of v
 View Solution
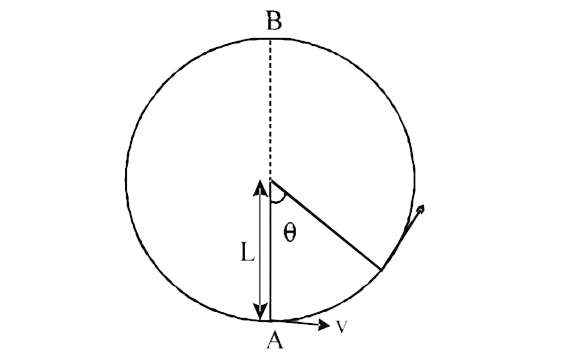
View SolutionA bob of mass M is suspended by a massless string of length L. The horizontal velocity v at position A is just sufficient to make it reach the point B. The angle θ at which the speed of the bob is half of that at A, satisfies
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A stone of mass 5 kg is tied to a string of length 10 m is whirled round in a horizontal circle. What is the maximum speed with which the stone can be whirled around if the string can withstand a maximum tension of 200 N?
A10ms−1B15ms−1C20ms−1D25ms−1
A particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
View SolutionA stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
View SolutionThree blocks with masses m , 2m and 3m are connected by strings, as shown in the figure. After an upward force F is applied on block m , the masses move upward at costant speed v . What is the net force on the block of mass 2m ? (g is the acceleration due to gravity). ltBrgt
 View Solution
View SolutionThree blocks with masses m , 2m and 3m are connected by strings, as shown in the figure. After an upward force F is applied on block m , the masses move upward at costant speed v . What is the net force on the block of mass 2m ? (g is the acceleration due to gravity). ltBrgt
 View Solution
View SolutionA particle of mass 'm' is moving in horizontal circle inside a smooth inverted fixed vertical cone above height 'h' from apex. Angle of cone is θ, then
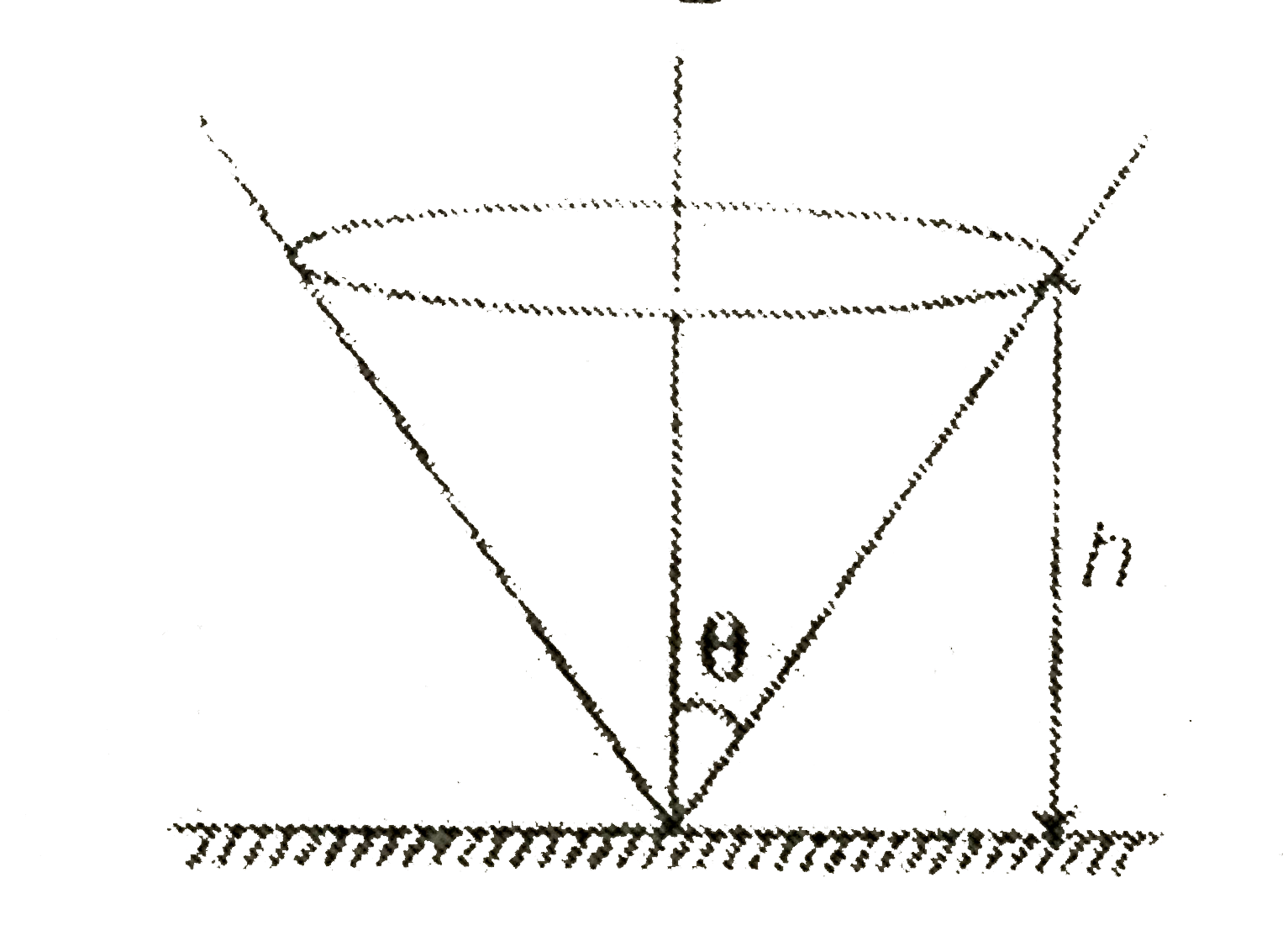 View Solution
View SolutionA block of mass 3M connected to a massless rod of length L lies at rest on a fixed frictionless table. A second block of mass M moving with speed v0 strikes the opposite end of the rod at right angle and sticks. The velocity of centre of mass of the system after collision is
_PHY_E05_239_Q01.png) View Solution
View SolutionA block of mass m is attached with a massless in string. Breaking strength of string is 4mg. Block is moving up. The maximum acceleration and maximum retardation of the block can be
 View Solution
View Solution

