When a perosn throws a meter stivk it is found that the centre of the stick is moving with speed 10m/s and left end stick with speed 20m/s. Both points move vertically upwards at that moment. Then angular speed the stick is :
20 rad/sec
10 rad/sec
30 rad/sec
none of these
The correct Answer is:A
To solve the problem of finding the angular speed of the stick when thrown, we can follow these steps:
Step 1: Understand the problem
We have a meter stick, and we know the speeds of two points on it: the center of the stick and the left end. The center of the stick moves with a speed Vc=10m/s and the left end moves with a speed Vp=20m/s. We need to find the angular speed ω of the stick.
Step 2: Define the distance from the center to the end of the stick
The length of the stick is 1 meter, so the distance from the center of the stick to either end is:
r=12m
Step 3: Use the relationship between linear speed and angular speed
The relationship between the linear speed of a point on a rotating object and its angular speed is given by:
V=Vc+rω
where V is the linear speed of the point, Vc is the speed of the center, r is the distance from the center to the point, and ω is the angular speed.
Step 4: Set up the equation for the left end of the stick
For the left end of the stick, we can write:
Vp=Vc+rω
Substituting the known values:
20=10+(12)ω
Step 5: Solve for ω
Rearranging the equation gives:
20−10=12ω
10=12ω
Multiplying both sides by 2:
ω=20rad/s
Conclusion
The angular speed of the stick is ω=20rad/s.
---
We have a meter stick, and we know the speeds of two points on it: the center of the stick and the left end. The center of the stick moves with a speed Vc=10m/s and the left end moves with a speed Vp=20m/s. We need to find the angular speed ω of the stick.
The length of the stick is 1 meter, so the distance from the center of the stick to either end is:
r=12m
The relationship between the linear speed of a point on a rotating object and its angular speed is given by:
V=Vc+rω
where V is the linear speed of the point, Vc is the speed of the center, r is the distance from the center to the point, and ω is the angular speed.
For the left end of the stick, we can write:
Vp=Vc+rω
Substituting the known values:
20=10+(12)ω
Rearranging the equation gives:
20−10=12ω
10=12ω
Multiplying both sides by 2:
ω=20rad/s
The angular speed of the stick is ω=20rad/s.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.529videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.5320videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.509videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)19videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
A system is shown in the figure. Block A is moving with 1m/s towards left. Wedge is moving with 1m/s towards right. Then speed of the block B will be :
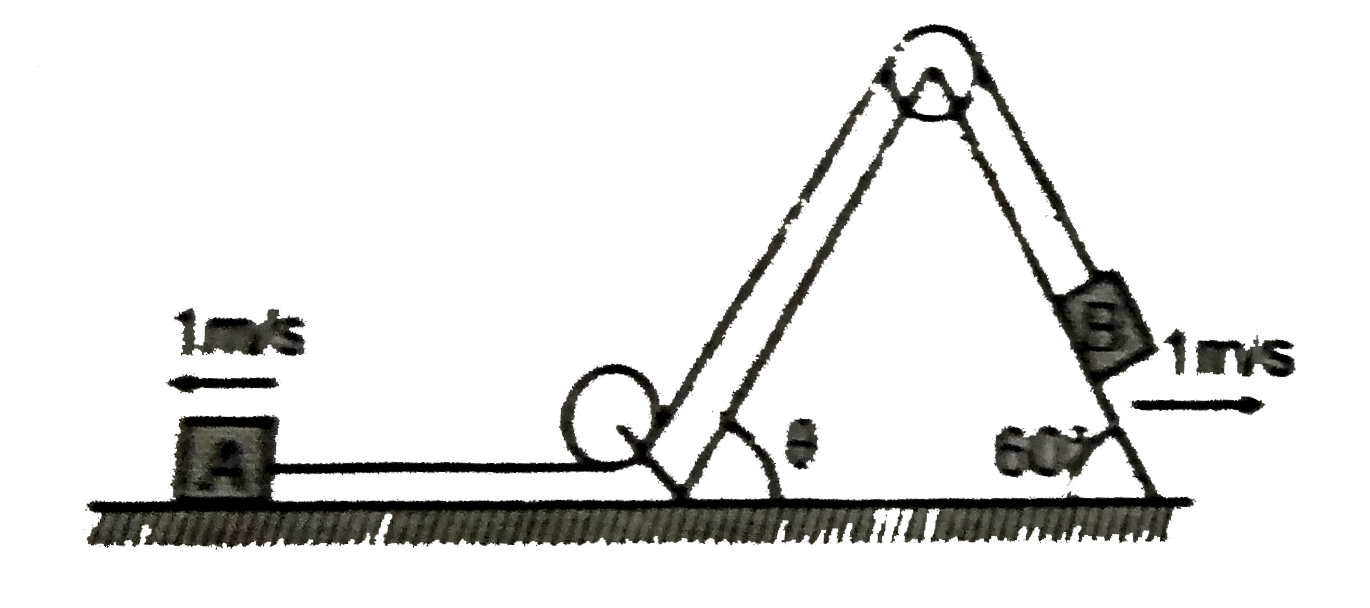 View Solution
View SolutionA highly elastic ball moving at a speed of 3m/s approaches a wall moving towards it with a speed of 3m/s. After the collision. the speed of the ball will be
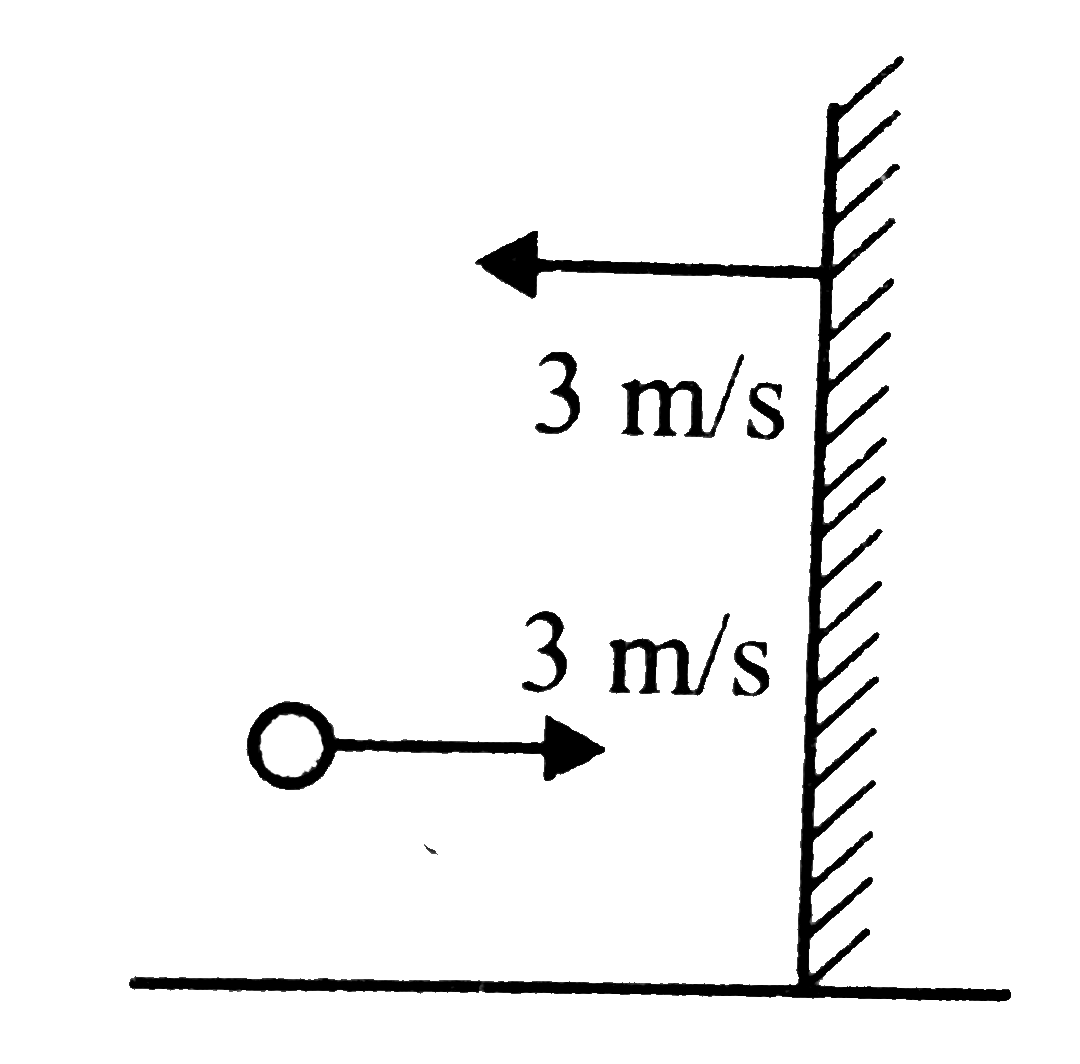 View Solution
View Solutiontruck is moving with a speed of 15 m/s. A car chasing this truck with a speed of 10 m/s fires a bullet at truck with muzzle velocity 90 km/h. The speed with which the bullet hit the truck is
View SolutionA metre stick is pivoted about its centre. A piece of wax of mass 20 g travelling horizontally and perpendicular to it at 5 m/s strikes and adheres to one end of the stick so that the stick starts to rotate in a horizontal circle. Given the moment of inertia of the stick and wax about the pivot is 0.02 kg m2, the initial angular velocity of the stick is :
View SolutionSpeed of an object moving in cirular path of radius 10 m with angular speed 2 rad/s is
View SolutionA car moves a distance of 100 m. It coveres first half with speed of 10 m/s and another half with speed of v m/s. If the average speed of car is 18 m/s, then value of v is
View SolutionA rod of mass 4m and length L is hinged at the mid point. A ball of mass 'm' moving with speed V in the plane of rod, strikes at the end at an angle of 45∘ and sticks to it. The angular velocity of system after collision is-
View SolutionA ball is thrown upward with speed 10 m/s from the top to the tower reaches the ground with a speed 20 m/s. The height of the tower is [Take g=10m/s2]
View SolutionA man standing on the edge of the terrace of a high rise building throws a stone, vertically up with at speed of 20m/s. Two seconds later, an identical stone is thrown vertically downwards with the same speed of 20m,. Then
View SolutionA car is moving at a speed of 40 m/s on a circular track of radius 400 m. this speed is increasing at the rate of 3 m/s2. The acceleration of car is
View Solution

