A rod of mass 4m and length L is hinged at the mid point. A ball of mass 'm' moving with speed V in the plane of rod, strikes at the end at an angle of and sticks to it. The angular velocity of system after collision is-
The correct Answer is:A
To solve the problem of finding the angular velocity of the system after the collision, we can follow these steps:
1. Identify the System:
- We have a rod of mass 4m and length L hinged at its midpoint.
- A ball of mass m is moving with speed V and strikes the end of the rod at an angle of 45∘.
2. Determine the Components of the Ball's Velocity:
- The ball strikes at an angle of 45∘, so we can resolve its velocity into two components:
- Vx=Vcos(45∘)=V√2
- Vy=Vsin(45∘)=V√2
3. Calculate the Initial Angular Momentum:
- The initial angular momentum Li of the ball about the hinge point (midpoint of the rod) can be calculated using the perpendicular distance from the hinge to the line of action of the ball's momentum.
- The distance from the hinge to the end of the rod is L2.
- The perpendicular component of the momentum is p_{\perpendicular} = m V_y = m \cdot \frac{V}{\sqrt{2}}.
- Therefore, the initial angular momentum is:
L_i = p_{\perpendicular} \cdot r = \left(m \cdot \frac{V}{\sqrt{2}}\right) \cdot \left(\frac{L}{2}\right) = \frac{mV L}{2\sqrt{2}}
4. Calculate the Moment of Inertia of the System:
- The moment of inertia I of the rod about the hinge is given by:
Irod=13⋅(4m)⋅L2=4mL23
- The moment of inertia of the ball about the hinge is:
Iball=m(L2)2=m⋅L24=mL24
- Therefore, the total moment of inertia I of the system after the collision is:
I=Irod+Iball=4mL23+mL24
- To combine these, find a common denominator (which is 12):
I=16mL212+3mL212=19mL212
5. Apply Conservation of Angular Momentum:
- Since there are no external torques acting on the system, the initial angular momentum Li must equal the final angular momentum Lf:
Li=Lf⟹mVL2√2=Iω
- Substituting for I:
mVL2√2=19mL212⋅ω
6. Solve for Angular Velocity ω:
- Cancel m and L from both sides:
V2√2=19L12⋅ω
- Rearranging gives:
ω=V2√2⋅1219L=6V19√2L
Final Answer:
ω=6V19√2L
- We have a rod of mass 4m and length L hinged at its midpoint.
- A ball of mass m is moving with speed V and strikes the end of the rod at an angle of 45∘.
- The ball strikes at an angle of 45∘, so we can resolve its velocity into two components:
- Vx=Vcos(45∘)=V√2
- Vy=Vsin(45∘)=V√2
- The initial angular momentum Li of the ball about the hinge point (midpoint of the rod) can be calculated using the perpendicular distance from the hinge to the line of action of the ball's momentum.
- The distance from the hinge to the end of the rod is L2.
- The perpendicular component of the momentum is p_{\perpendicular} = m V_y = m \cdot \frac{V}{\sqrt{2}}.
- Therefore, the initial angular momentum is:
L_i = p_{\perpendicular} \cdot r = \left(m \cdot \frac{V}{\sqrt{2}}\right) \cdot \left(\frac{L}{2}\right) = \frac{mV L}{2\sqrt{2}}
- The moment of inertia I of the rod about the hinge is given by:
Irod=13⋅(4m)⋅L2=4mL23
- The moment of inertia of the ball about the hinge is:
Iball=m(L2)2=m⋅L24=mL24
- Therefore, the total moment of inertia I of the system after the collision is:
I=Irod+Iball=4mL23+mL24
- To combine these, find a common denominator (which is 12):
I=16mL212+3mL212=19mL212
- Since there are no external torques acting on the system, the initial angular momentum Li must equal the final angular momentum Lf:
Li=Lf⟹mVL2√2=Iω
- Substituting for I:
mVL2√2=19mL212⋅ω
- Cancel m and L from both sides:
V2√2=19L12⋅ω
- Rearranging gives:
ω=V2√2⋅1219L=6V19√2L
ω=6V19√2L
Topper's Solved these Questions
Similar Questions
A uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is

View SolutionA rod of mass m and length l hinged at the centre is placed on a horizontal surface. A bullet of mass m moving with velocity v strikes the end A of the rod and gets embedded in it. The angular velocity with which the systems rotates about its centre of mass after the bullet strikes the rod

View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View SolutionA block of mass 3M connected to a massless rod of length L lies at rest on a fixed frictionless table. A second block of mass M moving with speed v0 strikes the opposite end of the rod at right angle and sticks. The velocity of centre of mass of the system after collision is
_PHY_E05_239_Q01.png)
View SolutionA wooden log of mass M and length L is hinged by a frictionless nail at O.A bullet of mass m strikes with velocity v and sticks to it. Find angular velocity of the system immediately after the collision aboutO.

View SolutionConsider the uniForm rod oF mass M=4m and length l pivoted about its centre. A mass m moving with velocity v making angle θ=π4 to the rod's long axis collides with one end oF the rod and sticks to it. The angular oFIGURE the rod-mass system just aFIGUREter the collision is:
View SolutionA particle of mass 2m moving with velocity v strikes a stationary particle of mass 3m and sticks to it . The speed of the system will be
View SolutionA uniform rod of mass m and length / is hinged at upper end. Rod is free to rotate in vertical plane. A bail of mass m moving horizontally with velocity vo collides at lower end of rod perpendicular to it and sticks to it. The minimum velocity of the ball such that combined system just completes the vertical circle will be
View SolutionA Iong slender rod of mass 2kg and length m is placed on a smooth horizontal table. Two particles of masses 2kg and 1kg strike the rod simultaneously and stick to the rod after collision as shown in fig.
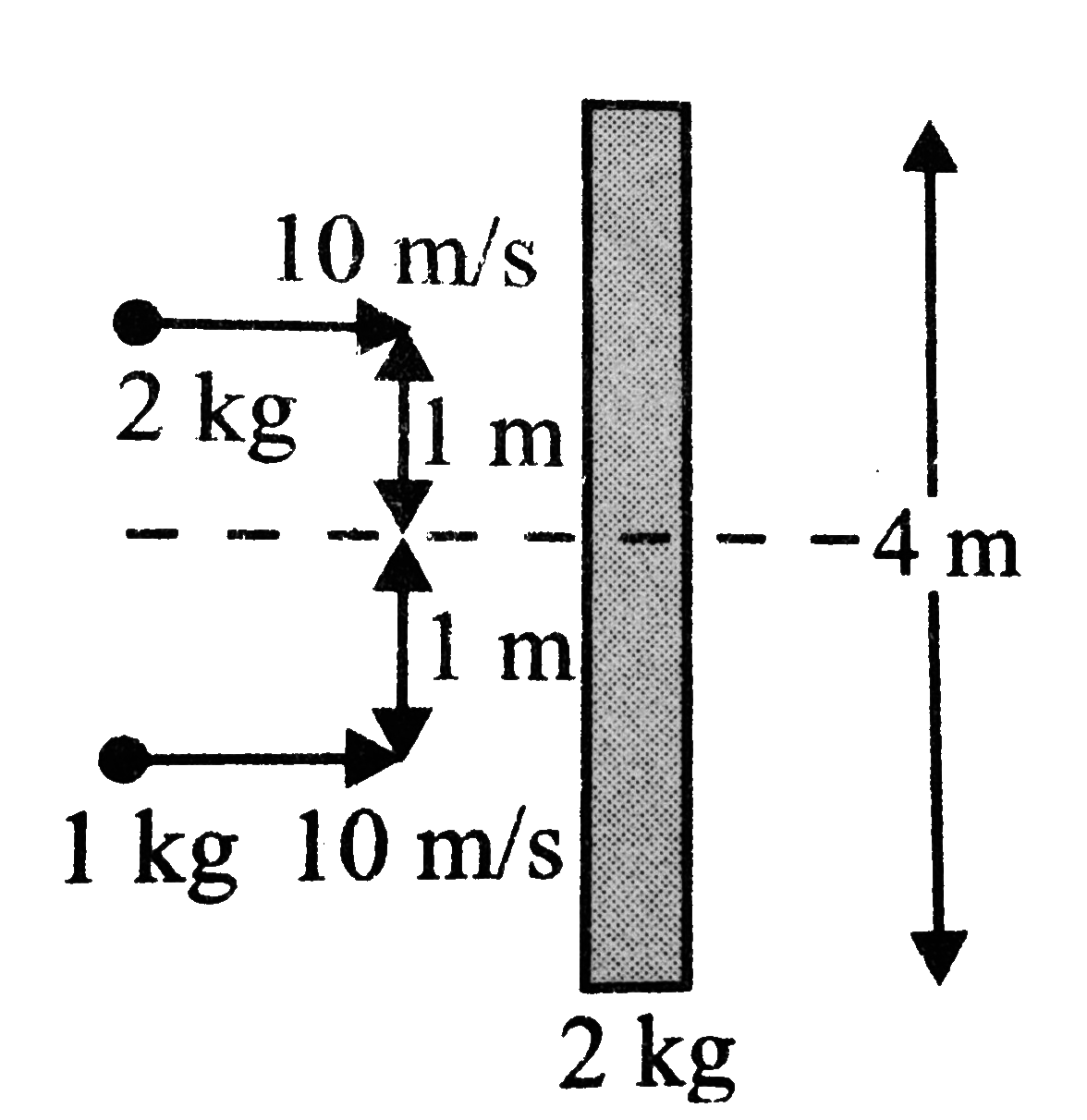
Angular velocity of the rod after collision is
View SolutionA bar of mass m and length l is in pure translational motion with its centre of mass moving with a velocity v. It collides and sticks to another identical bar at rest as shown in the figure. Assuming that after the collision the system of the two bars becomes one composite bar of length 2l, then the angular velocity of the composite bar will be
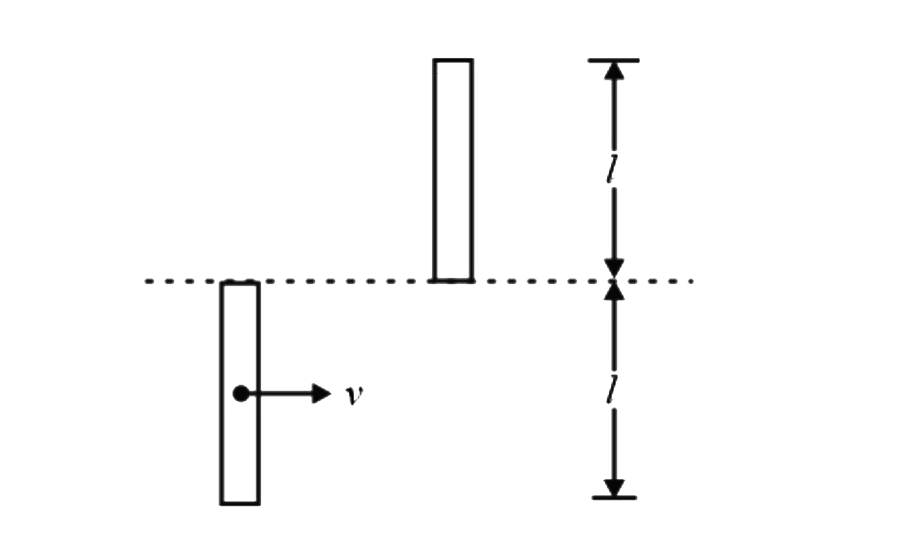
View Solution
