A thin superconducting (zero resistance) ring a held above a vertical long solenoid, as shown in the figure. The axis of symmetry of the ring is same to that of the solenoid. The cylindrically symmetric magnetic field around the ring can be described approximately in terms of the vertical and radial component of the magnetic field vector as Bz=B0(1−αz) and Br=B0βr, where B0,α and β are positive constants, and z & r are vertical and radial position coordinates, respectively, Initially plane of the ring is horizontal has no current flowing in it. When relreased, it starts to move downwards with its axis axis still vertical. Initial coordinates of the centre of the ring 'O' is z = 0 and r =0. In the given diagram point O is on the axis and slightly above the solenoid having vertical and radial position coordinates as (0,0) Ring has mass m, radius m, radius r0 and self inductance L. Assume the acceleration due to gravity as g.

Find the time period of SHM (for small displacement alon z-axis) of the ring.
1B0r20√2mLαβ
12B0r20√2mLαβ
1B0r20√mL3αβ
ring will not perform SHM
The correct Answer is:A
Total magnetic flux at any position
ϕ=Bzπr20−LI
Since, R=0, so ϕ=B0(1−αz)πr20−LI= constant
From initial condition (z=0,I=0), the value of constant is ϕ=B0πr20
Using the above equation the current in the ring I=1LB0απr20z
The lorentz foce acting on the ring (which can only be vertical because of the symmetry of the assembly) can be expressed as)
Fz=−B0I(z)2πr0=−2B20αβπ2r40zL=−kz
Equation of motion of the ring is maz=Fz−mg=−kz−mg
Equilibrium position
z0=−mg/kω0=√km.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.53
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.54
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.51
20 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
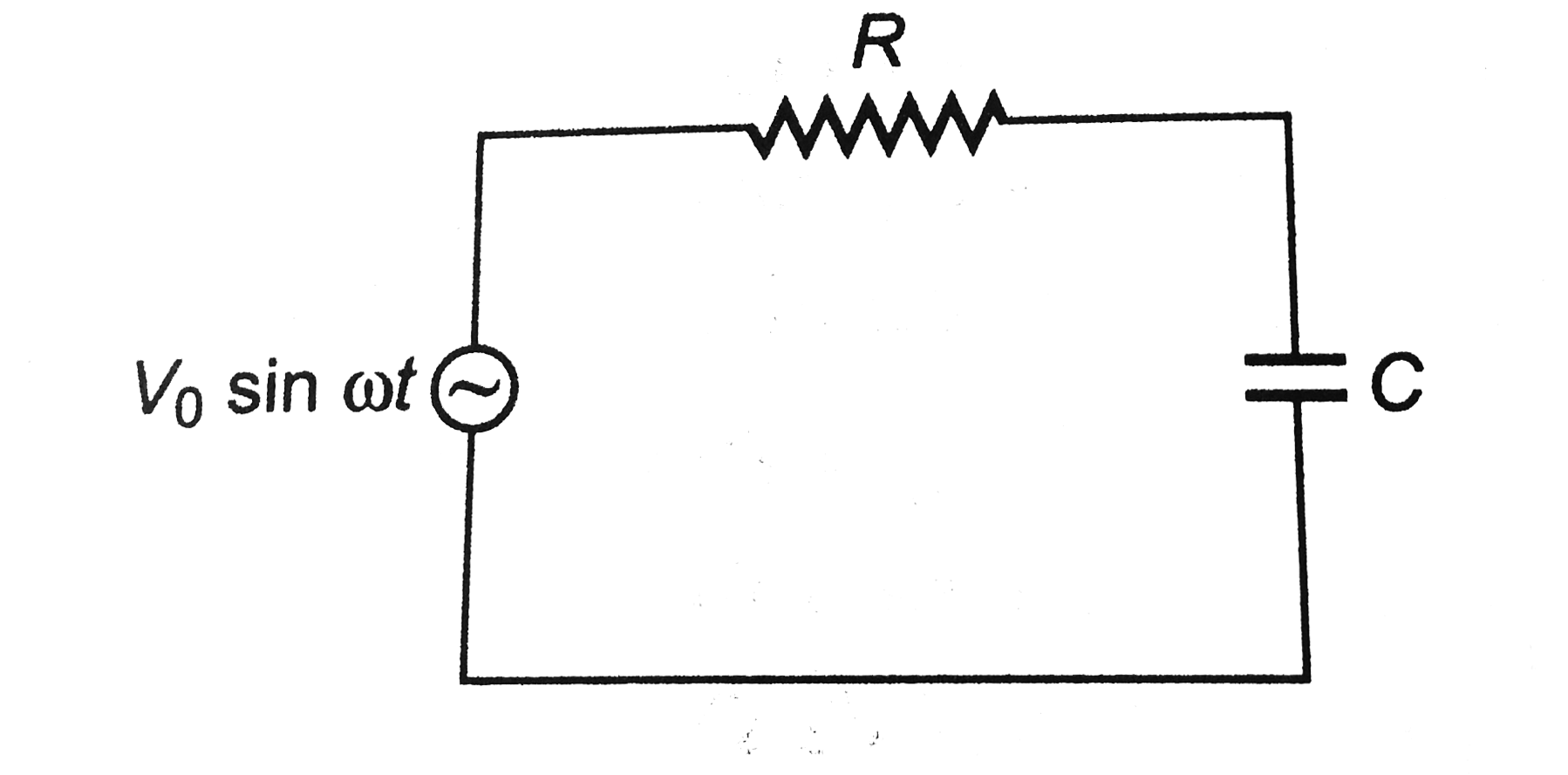
An AC voltage source V=V0sinωt is connected across resistance R and capacitance C as shown in figure. It is given that ωC=1R. The peak current is I0. If the angular frequency of the voltage source is changed to ω√3, then the new peak current in the circuit is
 .
.
View SolutionIn arrangement shown in figure, plane wavefront of monochromatic light of wavelength λ is incident on identical slits S1 and S2. There is another pair of indentical slits S3 and S4 which are having separation Z=λD2d Point O is on the screen at the common perpendicular bisector of S1S2 and S3S4.I1 is the intensity at point O Now the board having slits S3S4 is moved upward parallel to itself and perpendicular to line AO till slit S4 is on line AO and it is observed that now intensity at point O is I2 then I2I1 is :

View SolutionThe secondary coil of an ideal step down transformer is delivering 500 watt power at 12.5A current. If the ratio of turns in the primary to the secondary is 5:1 then the current flowing in the primary coil will be:
View SolutionA galvanometer having 30 divisions has a current sensitivity of 20μA/ division. It has a resistance of 5Ω How will you convert it into an ammeter measuring upto 1A ?
View SolutionAn electromagnetic wave of frequency υ=3 MHz passes from vacuum into a dielectric medium with permittivity ε=4. Then
View SolutionThe correct relation is (Where B_(H) = Horizontal component of earth's magnetic field, B_(V) = Vertical component of earth's magnetic field and B= Total intensity of earth's magnetic field)
View SolutionA metallic ring of field. If z is the radius l (ring being horizontal is falling under gravity in a region haivng a magnetic field. If z is the vertical direction, the z-component of magnetic field is B_(z) = B_(0) (1 + lambda z) . If R the resistance of the ring and if the ring falls with a velocity upsilon , find the energy lost in the resistance If the ring has reached a constant velocity, use the conservation of energy to determine upsilon in terms of m, B, lambda and acceleration due to gravity g.
View SolutionA direct current flows in a solenoid of length L and radius R,(Kgt gtR) , producing a magnetic field of magnetic B_(0) inside the solenoid .
View SolutionA thin superconducting (zero resistance) ring a held above a vertical long solenoid, as shown in the figure. The axis of symmetry of the ring is same to that of the solenoid. The cylindrically symmetric magnetic field around the ring can be described approximately in terms of the vertical and radial component of the magnetic field vector as B_(z) = B_(0)(1-alpha z) and B_(r) = B_(0) beta r , where B_(0),alpha and beta are positive constants, and z & r are vertical and radial position coordinates, respectively, Initially plane of the ring is horizontal has no current flowing in it. When relreased, it starts to move downwards with its axis axis still vertical. Initial coordinates of the centre of the ring 'O' is z = 0 and r =0. In the given diagram point O is on the axis and slightly above the solenoid having vertical and radial position coordinates as (0,0) Ring has mass m, radius m, radius r_(0) and self inductance L. Assume the acceleration due to gravity as g. Find the magnitude of current in the ring at a vertical position z.
View SolutionA thin superconducting (zero resistance) ring a held above a vertical long solenoid, as shown in the figure. The axis of symmetry of the ring is same to that of the solenoid. The cylindrically symmetric magnetic field around the ring can be described approximately in terms of the vertical and radial component of the magnetic field vector as B_(z) = B_(0)(1-alpha z) and B_(r) = B_(0) beta r , where B_(0),alpha and beta are positive constants, and z & r are vertical and radial position coordinates, respectively, Initially plane of the ring is horizontal has no current flowing in it. When relreased, it starts to move downwards with its axis axis still vertical. Initial coordinates of the centre of the ring 'O' is z = 0 and r =0. In the given diagram point O is on the axis and slightly above the solenoid having vertical and radial position coordinates as (0,0) Ring has mass m, radius m, radius r_(0) and self inductance L. Assume the acceleration due to gravity as g. Find the vertical coordinates z for equilibrium position of the ring.
View SolutionA thin superconducting (zero resistance) ring a held above a vertical long solenoid, as shown in the figure. The axis of symmetry of the ring is same to that of the solenoid. The cylindrically symmetric magnetic field around the ring can be described approximately in terms of the vertical and radial component of the magnetic field vector as B_(z) = B_(0)(1-alpha z) and B_(r) = B_(0) beta r , where B_(0),alpha and beta are positive constants, and z & r are vertical and radial position coordinates, respectively, Initially plane of the ring is horizontal has no current flowing in it. When relreased, it starts to move downwards with its axis axis still vertical. Initial coordinates of the centre of the ring 'O' is z = 0 and r =0. In the given diagram point O is on the axis and slightly above the solenoid having vertical and radial position coordinates as (0,0) Ring has mass m, radius m, radius r_(0) and self inductance L. Assume the acceleration due to gravity as g. Find the time period of SHM (for small displacement alon z-axis) of the ring.
View Solutionकिसी स्थान पर पृथ्वी के चुम्बकीय - क्षेत्र का क्षैतिज घटक B0 तथा ऊर्ध्वाधर घटक B0 परिणाम में बराबर हैं उस स्थान पर सम्पूर्ण तीव्रता का मान होगा -
View SolutionThe magnetic field on the axis of a circular current carrying conductor of radius r at a distance r from centre is Ba and the magnetic field at its centre is Bc. The value of Ba:Bc is
View Solutionr त्रिज्या की धारावाही कुंडली के केंद्र पर चुंबकीय क्षेत्र B0 है। इस कुंडली के अक्ष पर उसके केंद्र से कितनी दूरी पर चुंबकीय क्षेत्र 127B0 होगा ?
View SolutionA conducting ring of radius ris placed perpendicularly inside a time varying magnetic field given by B=B0+αl. B0 and a are positive constants. E.m.f. induced in the ring is
View SolutionThe magnetic field at the centre of a circular current carrying conductor of radius r is Bc . The magnetic field on its axis at a distance r from the centre is Ba. The value of Bc:Ba will be
View Solution
