An polaroid long cylindrical object with radius R has a charge distribution that depends upon distance r from the axis like this : ρ=ar+br2(r≤R, a and b are non zero constant, ρ is volume charge density). If electric field outside the cylinder is zero than value of ab is :
3R/4
−3R/4
−4R/3
4R/3
The correct Answer is:B
To solve the problem, we need to determine the ratio ab given the charge density distribution ρ=ar+br2 for a long cylindrical object with radius R, under the condition that the electric field outside the cylinder is zero.
1. Understand the Problem: We know that the electric field outside the cylinder is zero. According to Gauss's law, this implies that the total charge enclosed within a Gaussian surface (which is outside the cylinder) must be zero.
2. Set Up the Charge Density: The volume charge density is given by:
ρ(r)=ar+br2(0≤r≤R)
3. Calculate Total Charge Inside the Cylinder: The total charge Q inside the cylinder can be found by integrating the charge density over the volume of the cylinder:
Q=∫R0ρ(r)⋅dV
where dV=2πrdr (the differential volume element for a cylindrical shell).
4. Substituting for dV:
Q=∫R0(ar+br2)⋅(2πr)dr
Q=2π∫R0(ar2+br3)dr
5. Evaluate the Integral:
Q=2π(ar33+br44)R0
Q=2π(aR33+bR44)
6. Set Total Charge to Zero: Since the electric field outside the cylinder is zero, we set Q=0:
aR33+bR44=0
7. Rearranging the Equation:
aR33=−bR44
8. Finding the Ratio ab:
ab=−3R4
Final Answer:
The value of ab is:
ab=−3R4
ρ(r)=ar+br2(0≤r≤R)
Q=∫R0ρ(r)⋅dV
where dV=2πrdr (the differential volume element for a cylindrical shell).
Q=∫R0(ar+br2)⋅(2πr)dr
Q=2π∫R0(ar2+br3)dr
Q=2π(ar33+br44)R0
Q=2π(aR33+bR44)
aR33+bR44=0
aR33=−bR44
ab=−3R4
The value of ab is:
ab=−3R4
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.54
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.55
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.52
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
A solid sphere of radius R has a charge Q distributed in its volume with a charge density ρ=kra, where k and a are constants and r is the distance from its centre. If the electric field at r=R2 is 18 times that r=R, find the value of a.
View SolutionA very long uniformly charged cylinder (radius R) has a surface charge density σ . A very long uniformaly charged line charge( linear charge density λ) is placed along the ctlinder axis. If electric field intensity vector outside the cylinder is zerom then :
View SolutionFor spherically symmetrical charge distribution, electric field at a distance r from the centre of sphere is →E=kr7→r, where k is a constant. What will be the volume charge density at a distance r from the centre of sphere?
View SolutionA hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
View SolutionA long cylindrical volume (of radius R) contains a uniformly distributed charge of density ρ. Consider a point P inside the cylindrical volume at a distance x from its axis as shown in the figure. Here x can be more than or less than R. Electric field at point P is :

View SolutionA cylindrical space of radius R is filled with a uniform magnetic induction parallel to the axis of the cylinder. If B charges at a constant rate, the graph showin the variation of induced electric field with distance r from the axis of cylinder is
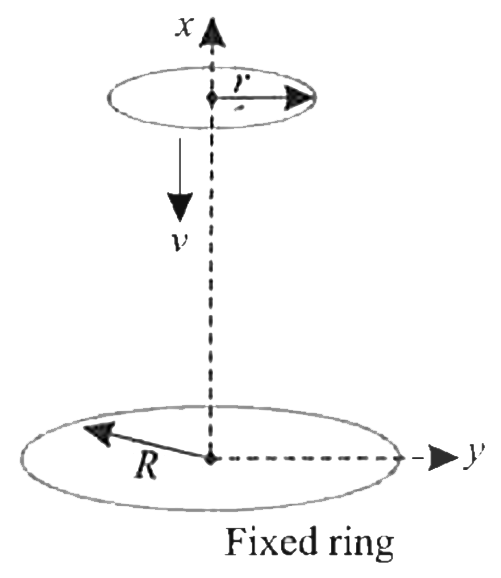
View SolutionA ring of radius R is placed in the plane its centre at origin and its axis along the x-asis and having uniformly distributed positive charge. A ring of radius r(<<R) and coaxial with the larger ring is moving along the axis with constant velcity , then the variation of electrical flux (ϕ) passing through the smaller ring with position will be best represent by :
View SolutionA solid non-conduction cylinder of radius R is charge such that volume charge density is proporation to r where r is distance from axis. The electric field E at a distance r(r<R) well depend on r as.
View SolutionA sphere of charges of radius R carries a positive charge whose volume chasrge density depends only on the distance r from the ball's centre as ρ=ρ0(1−rR), where ρ0 is constant. Assume epsilon as theh permittivity of space.
the maximum electric field intensity is
View SolutionA very long, solid insulating cylinder with radius R has a cylindrical hole with radius a bored along its entire length. The axis of the hole is at a distance b from the axis of the cylinder, where a<b<R (as shown in figure). The solid material of the cylinder has a uniform volume charge density ρ. Find the magnitude and direction of the electric field inside the hole, and show that this is uniform over the entire hole.
 .
.
View Solution
