A solid sphere of radius R has a charge Q distributed in its volume with a charge density ρ=kra, where k and a are constants and r is the distance from its centre. If the electric field at r=R2 is 18 times that r=R, find the value of a.
To solve the problem, we need to find the value of a given the electric field at r=R2 is 18 times the electric field at r=R. The charge density is given as ρ=kra.
1. Charge Density and Charge Enclosed:
The charge density is given by ρ=kra. To find the total charge Q enclosed within a sphere of radius R, we will integrate the charge density over the volume of the sphere:
Q=∫R0ρdV=∫R0kradV
The volume element in spherical coordinates is dV=4πr2dr. Therefore, we have:
Q=∫R0kra(4πr2)dr=4πk∫R0ra+2dr
2. Integrating:
The integral can be computed as follows:
∫R0ra+2dr=Ra+3a+3
Thus, the total charge Q becomes:
Q=4πk⋅Ra+3a+3=4πkRa+3a+3
3. Electric Field Inside the Sphere:
To find the electric field at r=R2, we need to calculate the charge enclosed within r=R2:
QR2=∫R20kra(4πr2)dr=4πk∫R20ra+2dr
Evaluating this integral:
QR2=4πk⋅(R2)a+3a+3=4πka+3⋅Ra+32a+3
4. Electric Field Calculation:
The electric field E at a distance r from the center of a uniformly charged sphere is given by:
E=14πϵ0Qenclosedr2
For r=R2:
E(R2)=14πϵ0⋅4πka+3⋅Ra+32a+3(R2)2
Simplifying this:
E(R2)=kRa+3ϵ0(a+3)⋅4R2⋅2a+3=8kRa+1ϵ0(a+3)2a
5. Electric Field at the Surface:
For r=R:
E(R)=14πϵ0⋅QR2=14πϵ0⋅4πkRa+3a+3R2=kRa+1ϵ0(a+3)
6. Setting Up the Equation:
According to the problem, we have:
E(R2)=18E(R)
Substituting the expressions we derived:
8kRa+1ϵ0(a+3)2a=18⋅kRa+1ϵ0(a+3)
Canceling kRa+1ϵ0(a+3) from both sides gives:
8⋅8=2a⟹64=2a⟹a=6
Final Answer:
The value of a is 6.
The charge density is given by ρ=kra. To find the total charge Q enclosed within a sphere of radius R, we will integrate the charge density over the volume of the sphere:
Q=∫R0ρdV=∫R0kradV
The volume element in spherical coordinates is dV=4πr2dr. Therefore, we have:
Q=∫R0kra(4πr2)dr=4πk∫R0ra+2dr
The integral can be computed as follows:
∫R0ra+2dr=Ra+3a+3
Thus, the total charge Q becomes:
Q=4πk⋅Ra+3a+3=4πkRa+3a+3
To find the electric field at r=R2, we need to calculate the charge enclosed within r=R2:
QR2=∫R20kra(4πr2)dr=4πk∫R20ra+2dr
Evaluating this integral:
QR2=4πk⋅(R2)a+3a+3=4πka+3⋅Ra+32a+3
The electric field E at a distance r from the center of a uniformly charged sphere is given by:
E=14πϵ0Qenclosedr2
For r=R2:
E(R2)=14πϵ0⋅4πka+3⋅Ra+32a+3(R2)2
Simplifying this:
E(R2)=kRa+3ϵ0(a+3)⋅4R2⋅2a+3=8kRa+1ϵ0(a+3)2a
For r=R:
E(R)=14πϵ0⋅QR2=14πϵ0⋅4πkRa+3a+3R2=kRa+1ϵ0(a+3)
According to the problem, we have:
E(R2)=18E(R)
Substituting the expressions we derived:
8kRa+1ϵ0(a+3)2a=18⋅kRa+1ϵ0(a+3)
Canceling kRa+1ϵ0(a+3) from both sides gives:
8⋅8=2a⟹64=2a⟹a=6
The value of a is 6.
Similar Questions
A solid non conducting sphere of radius R has a non-uniform charge distribution of volume charge density, ρ=ρ0rR, where ρ0 is a constant and r is the distance from the centre of the sphere. Show that : (i) the total charge on the sphere is Q=πρ0R3 (ii) the electric field inside the sphere has a magnitude given by, E=KQr2R4
View SolutionAn insulating solid sphere of the radius R is charged in a non - uniform manner such that the volume charge density ρ=Ar, where A is a positive constant and r is the distance from the centre. The potential difference between the centre and surface of the sphere is
View Solution
Knowledge Check
- Question 1 - Select One
A system consits of a uniformly charged sphere of radius R and a surrounding medium filled by a charge with the volume density ρ=αr, where α is a positive constant and r is the distance from the centre of the sphere. Find the charge of the sphere for which the electric field intensity E outside the sphere is independent of R.
Aα2ε0B2αε0C2παR2DNone of these
The region between two concentric spheres of radii 'a' and 'b', respectively (see figure), have volume charge density ρ=Ar, where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is:
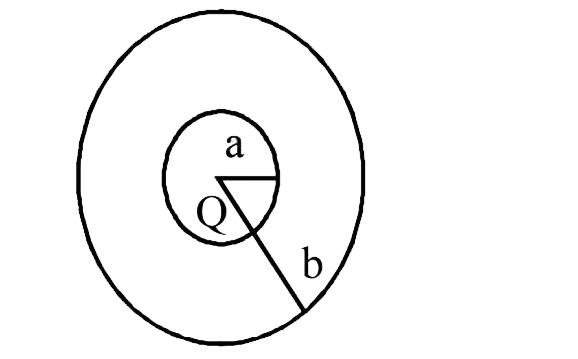 View Solution
View SolutionThe region between two concentric spheres of radii ‘a’ and ‘b’, respectively (see figure), has volume charge density p=Ar, where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is :
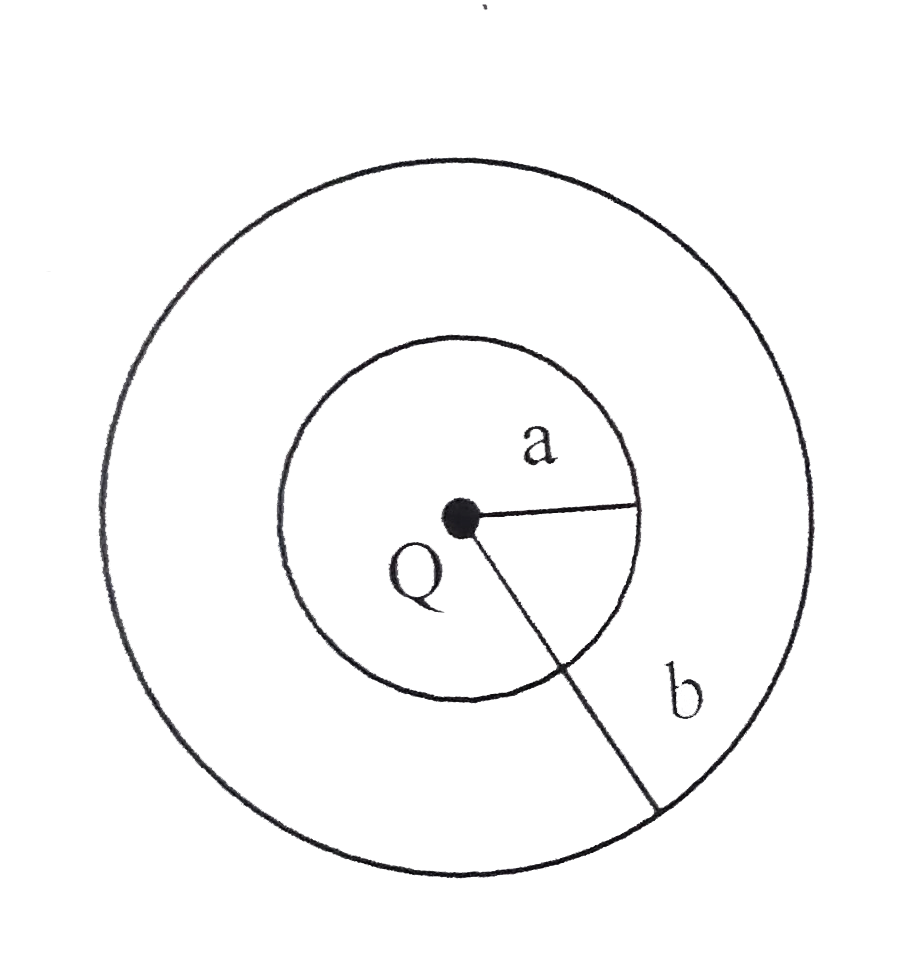 View Solution
View SolutionA sphere of radius R carries charge such that its volume charge density is proportional to the square of the distance from the centre. What is the ratio of the magnitude of the electric field at a distance 2 R from the centre to the magnitude of the electric field at a distance of R/2 from the centre?
View SolutionA solid sphere of radius R has charge q uniformly distributed over its volume. The distance from it surfce at which the electrostatic potential is equal to half of the potential at the centre is
View SolutionA solid sphere of radius R has charge q uniformly distributed over its volume. The distance from it surfce at which the electrostatic potential is equal to half of the potential at the centre is
View SolutionCharge is distributed within a sphere of radius R with a volume charge density p(r)=Ar2e−2r/a, where A and a are constants. If Q is the total charge of this charge distribution, the radius R is :
View SolutionA solid sphere of radius R has charge q uniformly distributed over its volume. The distance from its surface at which the electrostatic potential is equal to half of the potential at the centre is
View Solution

