A point charge placed on the axis of a uniformly charged disc experiences a force f due to the disc. If the charge density on the disc σ is, the electric flux through the disc, due to the point charge will be
2πfσ
f2πσ
f2σ
fσ
The correct Answer is:D
To solve the problem, we need to find the electric flux through a uniformly charged disc due to a point charge placed on its axis. Let's break down the solution step by step.
Step 1: Understand the Configuration
We have a uniformly charged disc with charge density σ and a point charge Q placed at a distance x along the axis of the disc. The goal is to find the electric flux Φ through the disc due to this point charge.
Step 2: Electric Field Due to the Disc
The electric field E at a point along the axis of a uniformly charged disc can be expressed as:
Ed=σ2ϵ0(1−x√R2+x2)
where R is the radius of the disc, σ is the surface charge density, and ϵ0 is the permittivity of free space.
Step 3: Calculate the Electric Flux
The electric flux Φ through the disc due to the electric field E can be calculated using the formula:
Φ=E⋅A
where A is the area of the disc. The area A of the disc is given by:
A=πR2
Thus, the electric flux through the disc becomes:
Φ=Ed⋅πR2
Step 4: Substitute the Electric Field Expression
Substituting the expression for Ed into the flux equation, we have:
Φ=(σ2ϵ0(1−x√R2+x2))⋅πR2
Step 5: Simplify the Expression
Now we can simplify the expression for electric flux:
Φ=σπR22ϵ0(1−x√R2+x2)
Step 6: Relate Flux to Force
From the previous parts, we know that the force F experienced by the point charge due to the electric field can be expressed as:
F=Q⋅Ed
Using the relationship between electric flux and force, we can express the flux in terms of force:
Φ=Fσ
Final Result
Thus, the electric flux through the disc due to the point charge is given by:
Φ=Fσ
We have a uniformly charged disc with charge density σ and a point charge Q placed at a distance x along the axis of the disc. The goal is to find the electric flux Φ through the disc due to this point charge.
The electric field E at a point along the axis of a uniformly charged disc can be expressed as:
Ed=σ2ϵ0(1−x√R2+x2)
where R is the radius of the disc, σ is the surface charge density, and ϵ0 is the permittivity of free space.
The electric flux Φ through the disc due to the electric field E can be calculated using the formula:
Φ=E⋅A
where A is the area of the disc. The area A of the disc is given by:
A=πR2
Thus, the electric flux through the disc becomes:
Φ=Ed⋅πR2
Substituting the expression for Ed into the flux equation, we have:
Φ=(σ2ϵ0(1−x√R2+x2))⋅πR2
Now we can simplify the expression for electric flux:
Φ=σπR22ϵ0(1−x√R2+x2)
From the previous parts, we know that the force F experienced by the point charge due to the electric field can be expressed as:
F=Q⋅Ed
Using the relationship between electric flux and force, we can express the flux in terms of force:
Φ=Fσ
Thus, the electric flux through the disc due to the point charge is given by:
Φ=Fσ
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.62
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.63
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.60
8 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
Find the electric field on the axis of a charged disc.
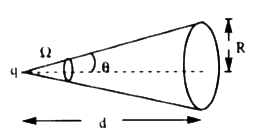
View SolutionA point charge q is placed at a distance d from the centre of a circular disc of radius R. Find electric flux flowing through the disc due to that charge
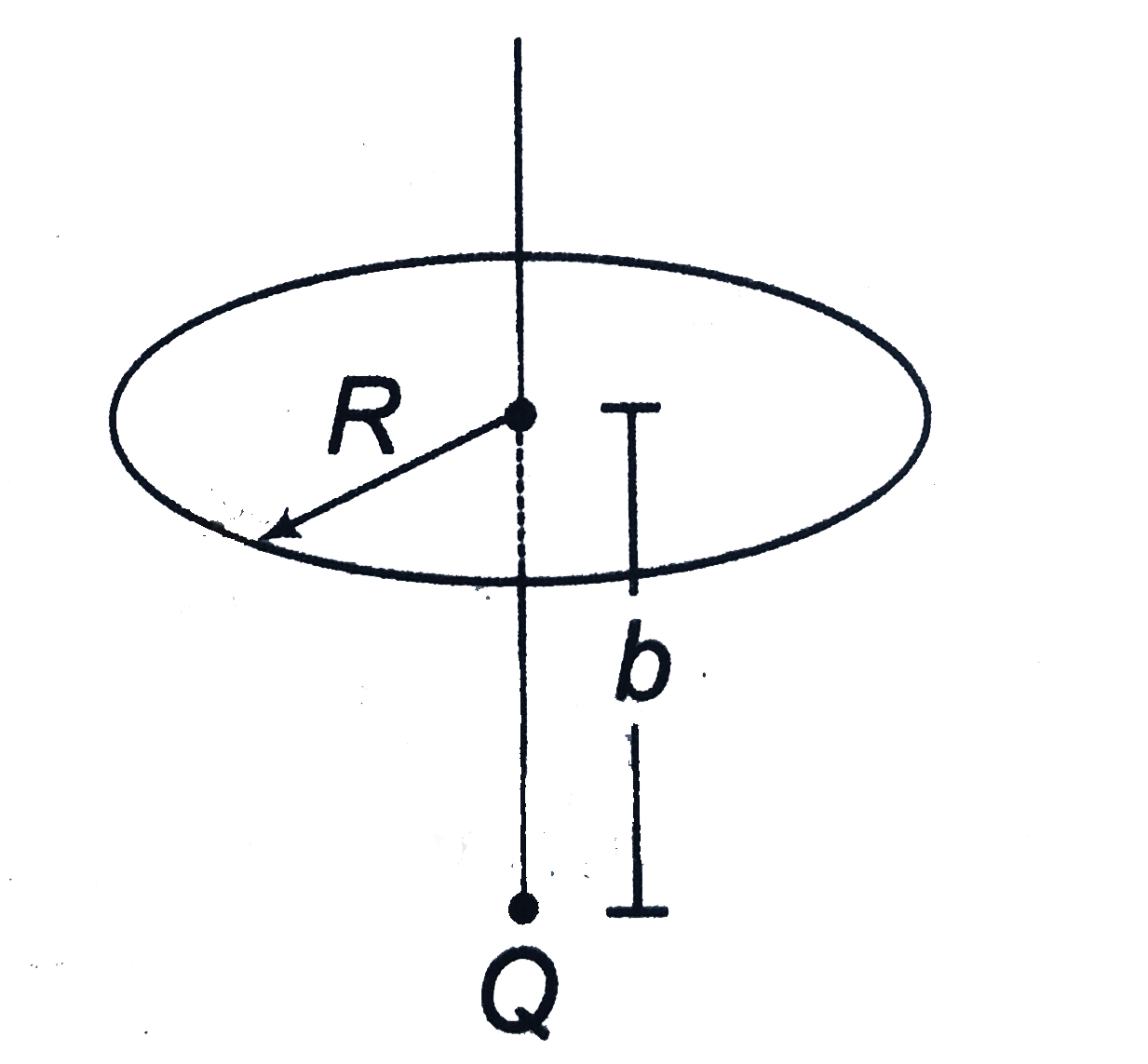
View SolutionA point charge Q is located on the axis of a disc of radius R at a distance b from the plane of the disc (figure). Show that if one-fourth of the electric flux from the charge passes through the disc, then R=√3b.
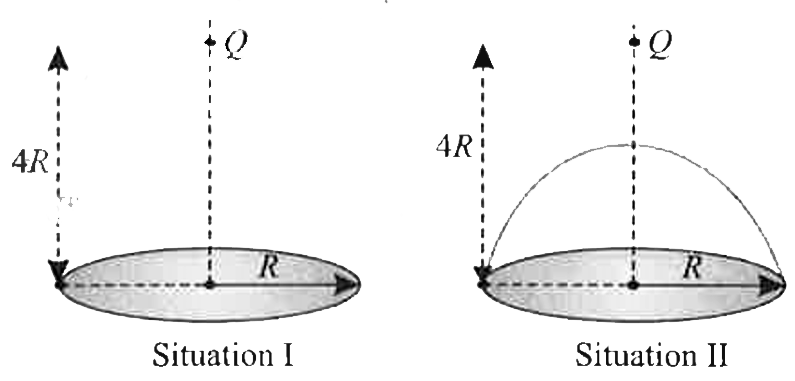
View SolutionA positive point charge Q is placed (on the axis of disc) at a distance of 4 R . Above the centre of a disc of radius R as shown in situation I. the magnitude of electric flux through the disc is (ϕ). Now a hemis pherical shell of radius R is placed over the disc. such that it forms a closed surface as shown in situation II. The flux through the curved suface in situation II taking direction of area vector along outward normal as positive is
View SolutionA charge +Q is placed on middle of edge of the cube.Then electric flux through cube due to field of charge +Q is
View SolutionA point charge Q is located on the axis of a disc of radius R at a distance b from the plane of the disk. If one - fourth of the electric flux from the charge passes through the disk, then R=√kb. Find k.

View SolutionA point charge q is placed at a distance r from a very long charged thread of unoform linear charge density λ. Find out total electric force experienced by the line charge due to the point charge. (Neglect gravity).
View SolutionA uniformly charged square plate having side L carries a uniform surface charge density σ. The plate lies in the y−z plane with its centre at the origin. A point charge q lies on the x-axis. The flux of the electric field of q through the plate is ϕ0, while the foce on the point charge q due to the plate is F0, along the x-axis. Then,
View SolutionA point charge q is placed at the origin . How does the electric field due to the charge very with distance r from the origin ?
View SolutionDerive an expression for electric field intensity at a point due to point charge.
View Solution