Moment of inertia of an ellipse shaped wire of mass 'm', semimajor axis 'a' about an axis passing through the centre and perpendicular to the plane of wire can be :
ma2
1.2ma2
1.4ma2
0.6ma2
The correct Answer is:D
To find the moment of inertia of an ellipse-shaped wire of mass 'm' and semi-major axis 'a' about an axis passing through the center and perpendicular to the plane of the wire, we can follow these steps:
Step 1: Understand the Geometry
The ellipse has a semi-major axis 'a' and a semi-minor axis 'b'. For the moment of inertia calculation, we need to visualize the ellipse and how it relates to a circle of radius 'a'.
Step 2: Moment of Inertia of a Circle
The moment of inertia I of a circular wire of mass m and radius a about an axis perpendicular to its plane through its center is given by:
Icircle=ma2
Step 3: Compare the Ellipse with the Circle
The ellipse can be thought of as a stretched circle. The points on the ellipse are at a distance less than or equal to 'a' from the center. Therefore, the moment of inertia of the ellipse will be less than that of the circle because the mass distribution is not as far from the axis of rotation compared to the circle.
Step 4: Moment of Inertia of the Ellipse
The moment of inertia I of the ellipse about the same axis can be expressed in terms of the moment of inertia of the circle:
Iellipse<Icircle=ma2
This implies that the moment of inertia of the ellipse is less than ma2.
Step 5: Conclusion
Since the moment of inertia of the ellipse is less than that of the circle, we can conclude that the moment of inertia of the ellipse-shaped wire is:
Iellipse<ma2
Final Answer
The moment of inertia of the ellipse-shaped wire of mass 'm' and semi-major axis 'a' about an axis passing through the center and perpendicular to the plane of the wire can be represented as:
Iellipse<ma2
The ellipse has a semi-major axis 'a' and a semi-minor axis 'b'. For the moment of inertia calculation, we need to visualize the ellipse and how it relates to a circle of radius 'a'.
The moment of inertia I of a circular wire of mass m and radius a about an axis perpendicular to its plane through its center is given by:
Icircle=ma2
The ellipse can be thought of as a stretched circle. The points on the ellipse are at a distance less than or equal to 'a' from the center. Therefore, the moment of inertia of the ellipse will be less than that of the circle because the mass distribution is not as far from the axis of rotation compared to the circle.
The moment of inertia I of the ellipse about the same axis can be expressed in terms of the moment of inertia of the circle:
Iellipse<Icircle=ma2
This implies that the moment of inertia of the ellipse is less than ma2.
Since the moment of inertia of the ellipse is less than that of the circle, we can conclude that the moment of inertia of the ellipse-shaped wire is:
Iellipse<ma2
The moment of inertia of the ellipse-shaped wire of mass 'm' and semi-major axis 'a' about an axis passing through the center and perpendicular to the plane of the wire can be represented as:
Iellipse<ma2
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.6710videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.689videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.659videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)19videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionThe moment of inertia of a solid cylinder of mass M, length 2R and radius R about an axis passing through the centre of mass and perpendicular to the axis of the cylinder is I1 and about an axis passing through one end of the cylinder and perpendicular to the axis of cylinder is I2
View SolutionThe moment of inertia of a uniform semicircular wire of mass m and radius r, about an axis passing through its centre of mass and perpendicular to its plane is mr2(−kπ2). Find the value of k.
View SolutionThe moment of inertia of a thin square plate ABCD of uniform thickness about an axis passing through the centre O and perpendicular to plate is
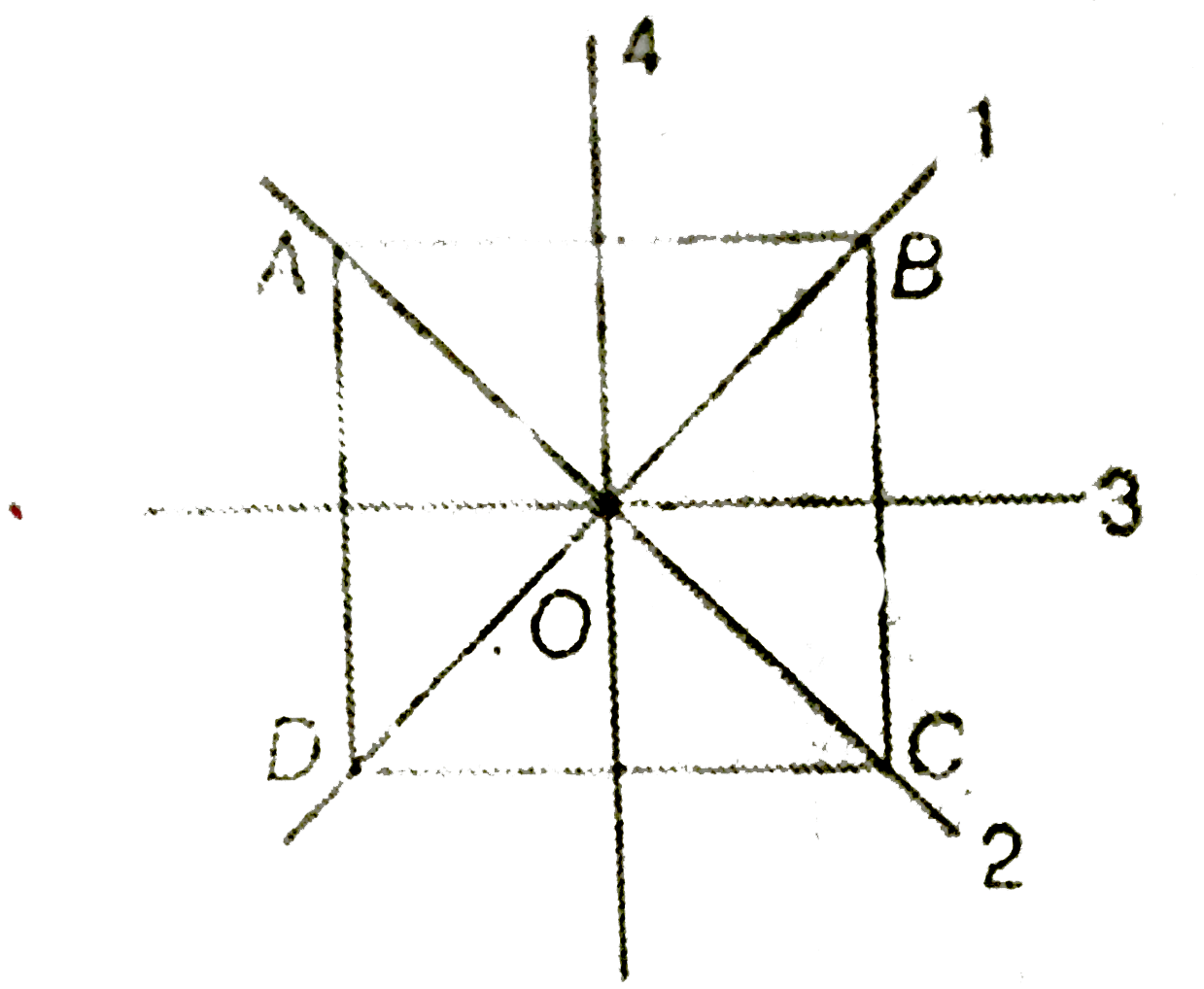 View Solution
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionThe moment of inertia of a uniform semicircular wire of mass M and radius R about an axis passing through its centre of mass and perpendicular to its plane is xMR210. Find the value of x? (Take π2=10)
View SolutionMoment of inertia of a thin rod of mass m and length l about an axis passing through a point l/4 from one end and perpendicular to the rod is
View SolutionCalculate the moment of inertia of a rectangular frame formed by uniform rods having mass m each as shown in about an axis passing through its centre and perpendicular to the plane of frame. Also find moment of inertia about an axis passing through PQ ?
 View Solution
View SolutionCalculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View SolutionCalculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View Solution

