The distance between two moving particles P and Q at any time is a.If vr be their relative velocity and if u and v be the components of vr, along and perpendicular to PQ.The closest distance between P and Q and time that elapses before they arrive at their nearest distance is
av1v2
av2v2
avv21
avv22
The correct Answer is:A
To solve the problem, we need to find the closest distance between two moving particles P and Q and the time that elapses before they arrive at their nearest distance.
1. Understanding the Setup:
- Let the distance between the two particles P and Q at any time be A.
- The relative velocity vr of the two particles can be resolved into two components:
- u: the component of vr along the line joining P and Q (PQ).
- v: the component of vr perpendicular to PQ.
2. Finding the Closest Distance:
- The closest distance between the two particles occurs when the line connecting them is perpendicular to the relative velocity vector.
- This closest distance can be represented as QR, where QR is the perpendicular distance from the line of motion to the point of closest approach.
- Using trigonometry, we can express QR in terms of A and the angle α between the relative velocity and the line joining P and Q:
QR=Acos(α)
3. Finding the Time to Closest Approach:
- The time T taken to reach the closest distance is given by the formula:
T=DistanceVelocity
- Here, the distance is QR and the velocity is the component of the relative velocity perpendicular to PQ, which is v.
- Therefore, we can write:
T=QRv=Acos(α)v
4. Relating cos(α) to the Relative Velocity:
- From the triangle formed by the components of the relative velocity, we can express cos(α) as:
cos(α)=vvr
- Substituting this back into the time equation gives:
T=A⋅vvrv=Avr
5. Final Expression:
- The closest distance QR can be expressed as:
QR=A⋅vvr
- The time T taken to reach this closest distance is:
T=Avr
Conclusion:
- The closest distance between particles P and Q is A⋅vvr.
- The time elapsed before they arrive at their nearest distance is Avr.
- Let the distance between the two particles P and Q at any time be A.
- The relative velocity vr of the two particles can be resolved into two components:
- u: the component of vr along the line joining P and Q (PQ).
- v: the component of vr perpendicular to PQ.
- The closest distance between the two particles occurs when the line connecting them is perpendicular to the relative velocity vector.
- This closest distance can be represented as QR, where QR is the perpendicular distance from the line of motion to the point of closest approach.
- Using trigonometry, we can express QR in terms of A and the angle α between the relative velocity and the line joining P and Q:
QR=Acos(α)
- The time T taken to reach the closest distance is given by the formula:
T=DistanceVelocity
- Here, the distance is QR and the velocity is the component of the relative velocity perpendicular to PQ, which is v.
- Therefore, we can write:
T=QRv=Acos(α)v
- From the triangle formed by the components of the relative velocity, we can express cos(α) as:
cos(α)=vvr
- Substituting this back into the time equation gives:
T=A⋅vvrv=Avr
- The closest distance QR can be expressed as:
QR=A⋅vvr
- The time T taken to reach this closest distance is:
T=Avr
- The closest distance between particles P and Q is A⋅vvr.
- The time elapsed before they arrive at their nearest distance is Avr.
Topper's Solved these Questions
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - MCQ_TYPE
27 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - COMPREHENSION_TYPE
19 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
Similar Questions
The displacement-time graphs of two particles P and Q are as shown in the figure. The ratio of their velocities VP and VQ will be
View SolutionTwo particles start moving from the same point along the same straight line. The first moves with constant velocity v and the second with constant acceleration a. During the time that elapses before the sound catches the first, the greatest distance between the particle is.
View SolutionTwo particles are moving with velocities v1andv2 . Their relative velocity is the maximum, when the angle between their velocities is
View SolutionTwo points of a rod move with velocity 3v and v perpendicular to the rod and in the same direction. Separated by a distance r. Then the angular velocity of the rod is :
View SolutionLet S be the set of all points in a plane and R be a relation on S defines as R={(P,Q): distance between PandQ is less than 2 units} Show that R is reflexive and symmetric but not transitive.
View SolutionLet S be the set of all points in a plane and R be a relation on S defines as R={(P,Q): distance between PandQ is less than 2 units} Show that R is reflexive and symmetric but not transitive.
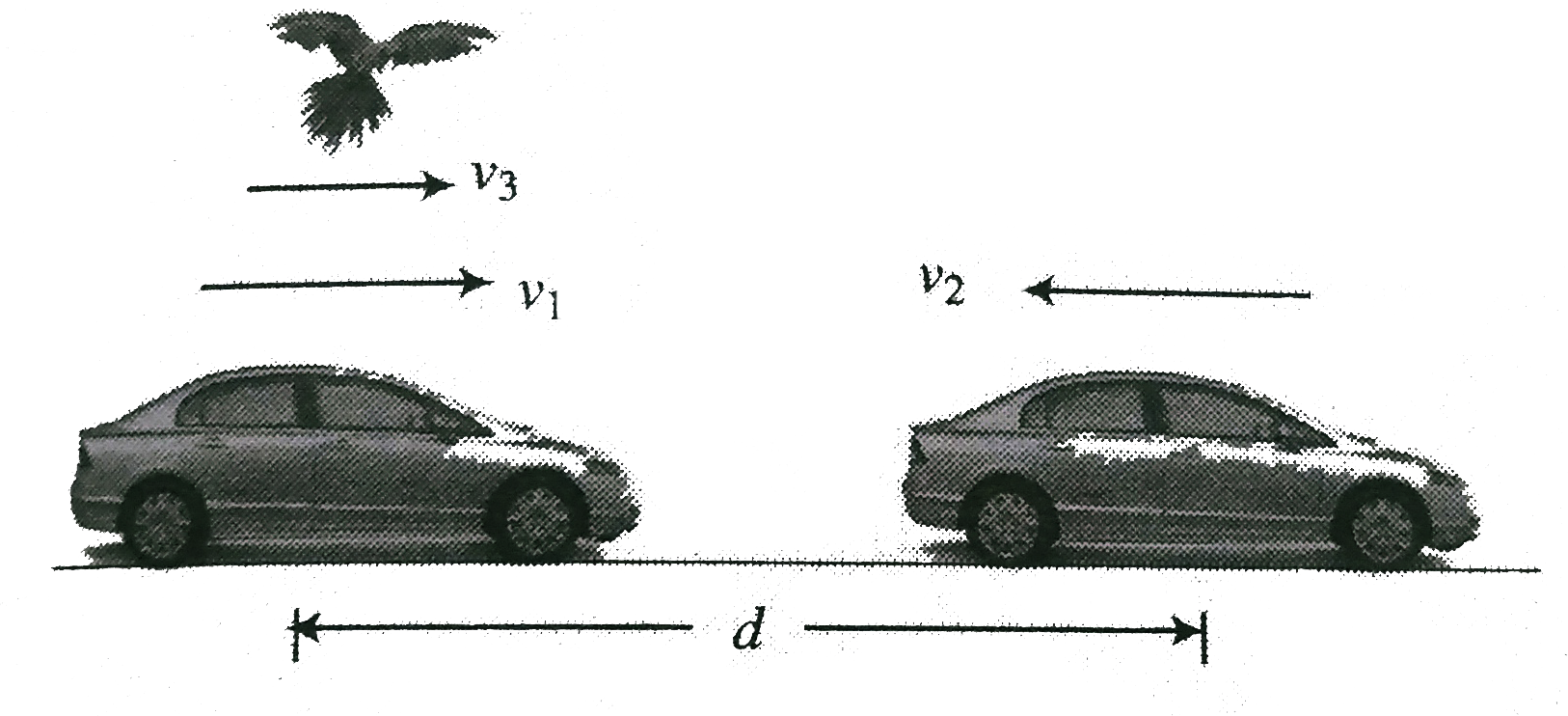
View SolutionA bird flies to and fro between two cars wich move with velocities v1 and v2, If the speed of the bird is v3 and the initial distance ofseparation between then is d, find the total distance covered bythe bird till the cars meet.
 .
.
View SolutionA : for a moving particle distance can never be negative or zero.
R : Distance is a scalar quantity and never decreases with time for moving object.
View SolutionA particle P of charge q and m , is placed at a point in gravity free to move. Another particle Q, of same charge and mass , is projected from a distance r from P with an initial speed v0 towards P , initial the distance between P and Q decreases and then increases.
The potential energy of the system of particles P and Q, at closest separation is
View SolutionTwo particles p and q located at distances rp and rq respectively from the centre of a rotating disc such that rp>rq.
View Solution
