A horizontal pipe carries water in the positive direction of x. Small identical holes are made at three different places along the pipe such that streams of water from them come out vertically upwards. The height upto which the water stream rise from the three holes
increase in the +Ve x-direction
decreases in the +ve x-direction
are the same in all
are the same for the first two and less for the third hole
The correct Answer is:C
To solve the problem of determining the height to which water streams rise from three holes in a horizontal pipe, we will use Bernoulli's theorem. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Setup
We have a horizontal pipe carrying water, and there are three holes made at different points along the pipe. Water flows out of these holes vertically upwards.
Step 2: Apply Bernoulli's Theorem
According to Bernoulli's theorem for a fluid flowing in a horizontal direction, the equation can be expressed as:
P+12ρv2=constant
where:
- P is the pressure,
- ρ is the density of the fluid (water in this case),
- v is the velocity of the fluid.
Step 3: Analyze the Flow
Since the pipe is horizontal, the gravitational potential energy term does not come into play. The pressure and kinetic energy terms are the only ones we need to consider.
Step 4: Consider the Effect of Holes
When water exits the holes, it will rise to a certain height due to the pressure at that point. The height h to which the water rises can be related to the pressure and velocity using the principle of conservation of energy.
Step 5: Determine Pressure and Velocity at Holes
If the velocity of the water is the same at all three holes (which is true since the cross-sectional area of the pipe does not change), then the pressure at all three holes will also be the same. This is because, according to Bernoulli’s principle, if the velocity remains constant, the pressure must also remain constant.
Step 6: Conclude the Height of Water Rise
Since the pressure is the same at all three holes and the velocity of the water is also the same, the height to which the water rises from each hole will be identical. Thus, the height h will be the same for all three holes.
Final Answer
The height to which the water streams rise from the three holes is the same.
We have a horizontal pipe carrying water, and there are three holes made at different points along the pipe. Water flows out of these holes vertically upwards.
According to Bernoulli's theorem for a fluid flowing in a horizontal direction, the equation can be expressed as:
P+12ρv2=constant
where:
- P is the pressure,
- ρ is the density of the fluid (water in this case),
- v is the velocity of the fluid.
Since the pipe is horizontal, the gravitational potential energy term does not come into play. The pressure and kinetic energy terms are the only ones we need to consider.
When water exits the holes, it will rise to a certain height due to the pressure at that point. The height h to which the water rises can be related to the pressure and velocity using the principle of conservation of energy.
If the velocity of the water is the same at all three holes (which is true since the cross-sectional area of the pipe does not change), then the pressure at all three holes will also be the same. This is because, according to Bernoulli’s principle, if the velocity remains constant, the pressure must also remain constant.
Since the pressure is the same at all three holes and the velocity of the water is also the same, the height to which the water rises from each hole will be identical. Thus, the height h will be the same for all three holes.
The height to which the water streams rise from the three holes is the same.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Examples22videos
FLUID MECHANICS
- BOOK - RESONANCE ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Board Level Exercise18videos
FLUID MECHANICS
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise52videos
ELECTROSTATICS
- BOOK - RESONANCE ENGLISHCHAPTER - FULL TEST 1EXERCISE - Exercise30videos
FULL TEST 1
Similar Questions
Water pours out rate of Q from a tap, into a cylindrical vessel of radius r. The rate at which the height of water level rises the height is h, is
View SolutionA rectangular tank is placed on a horizontal ground and is filled with water to a height H above the base. A small hole is made on one vertical side at a depth D below the level of the water in the tank. The distance x from the bottom of the tank at which the water jet from the tank will hit the ground is
View Solution
Knowledge Check
- Question 1 - Select One
A water barrel stands on a table of height h. If a small holes is punched in the side of the barrel at its base, it is found that the resultant stream of water strikes the ground at a horizontal distance R from the table. What is the depth of water in the barrel?
AR2hBR22hCR24hD4R2h
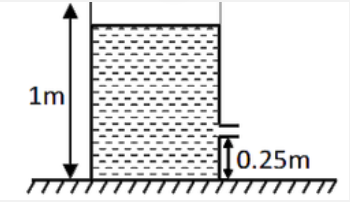
If a small orifice is made at a height of 0.25 m from the ground, the horizontal range of water stream will be : -
 View Solution
View SolutionA hose lying on the ground shoots a stream of water upward at an angle of 60∘ to the horizontal with the velocity of 16ms−1. The height at which the water strikes the wall 8m away is.
View SolutionIn a garden a spherical sprinkler is used at the end of the lose from which the speed of the flowing water is the same to every direction. The water beam which is directed vertically upward reaches a height of h. Once the sprinkler is placed to the ground and at another time ti a height of h. By what factor will the watered area of greater in the second case ? (Neglect air resistance and consider the pressure in the sprinkler constant.)
View SolutionTwo particles are simultaneously thrown in horizontal direction from two points on a riverbank, which are at certain height above the water surface. The initial velocities of the particles are v1=5m/sandv2=7.5m/s respectively. Both particles fall into the water at the same time. First particles enters the water at a point s = 10 m from the bank. Determine
(a) the time of flight of the two particles,
(b) the height from which they are thrown,
(c) the point where the second particle falls in water.View SolutionWater level is maintained ina cylindrical vessel up to a fixed height H. The vessel is kept on a horizontal plane. At what height above the bottom should a hole be made in the vessel so that the water stream coming out of the hole strikes the horizontal plane at the greatest distance from the vessel.
 View Solution
View SolutionOn the opposite sides of vertical vessel filled with water, two identical holes are opened. If area of cross-section for each is a and difference of height of these two is h and p is density of water, then force on the vessel is
View SolutionWater is filled to a height of 2.5m in a container lying rest on a horizontal surface as shown in the figure. The bottom of the container is square shaped of side √3 and its top is open. There is a very small hole in the vertical wall of the container near the bottom. A small cap closes the hole. The hole gets opened when pressure near the bottom becomes more than 4×104 pascal
a, What minimum acceleration can be given to the container in the positive x-direction so that the cap will come out of the hole? Assume water does not spill out of container when the container accelerates.
Find the velocity of efflux as soon as the container starts moving with the acceleration calculated in part a. of the question.
 View Solution
View Solution

