The total power dissipated in watts in the circuit shown here is

4W
16 W
40 W
54 W
The correct Answer is:D
The resistance of 6Ω and 3Ω are in parallel in the given circuit, their equivalent resistance is 1R1=16+13=1+26=12
or R1=2Ω
Again R1 is in series with 4Ω resistance hence
R=R1+4=2+4=6Ω
Thus, the total dissipated in the circuit
p=V2R
Here V=18V,R=6Ω
Thus, p=(18)26=54W
Topper's Solved these Questions
Similar Questions
The power dissipated in the circuit shown in the figure is 30 W. The value of R is
View SolutionPower factor of the circuit shown here is

View SolutionThe power dissipated in the circuit shown in the is 30 watts. The value of R is
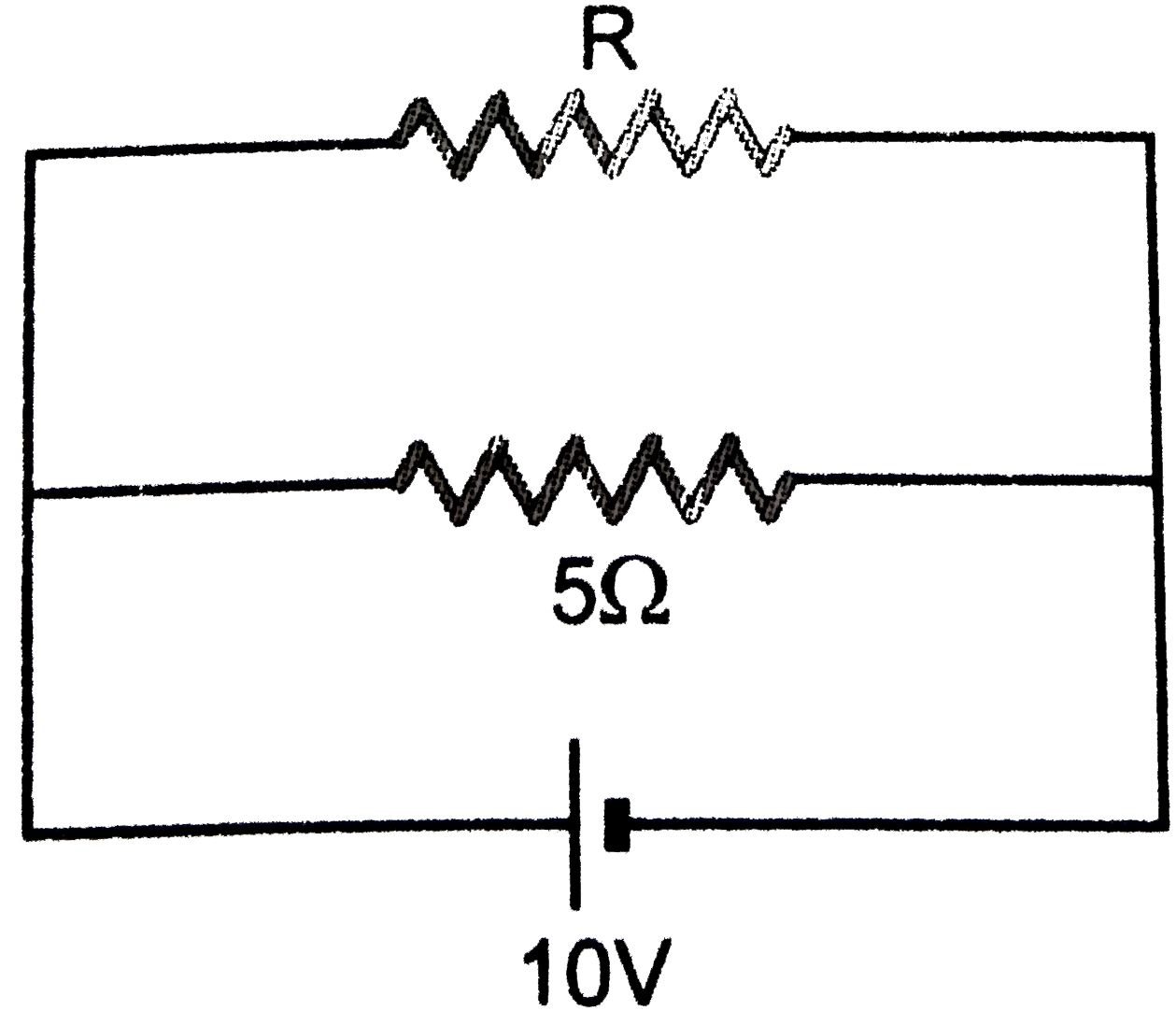
View SolutionThe power dissipated in the circuit shown in the is 30 watts. The value of R is

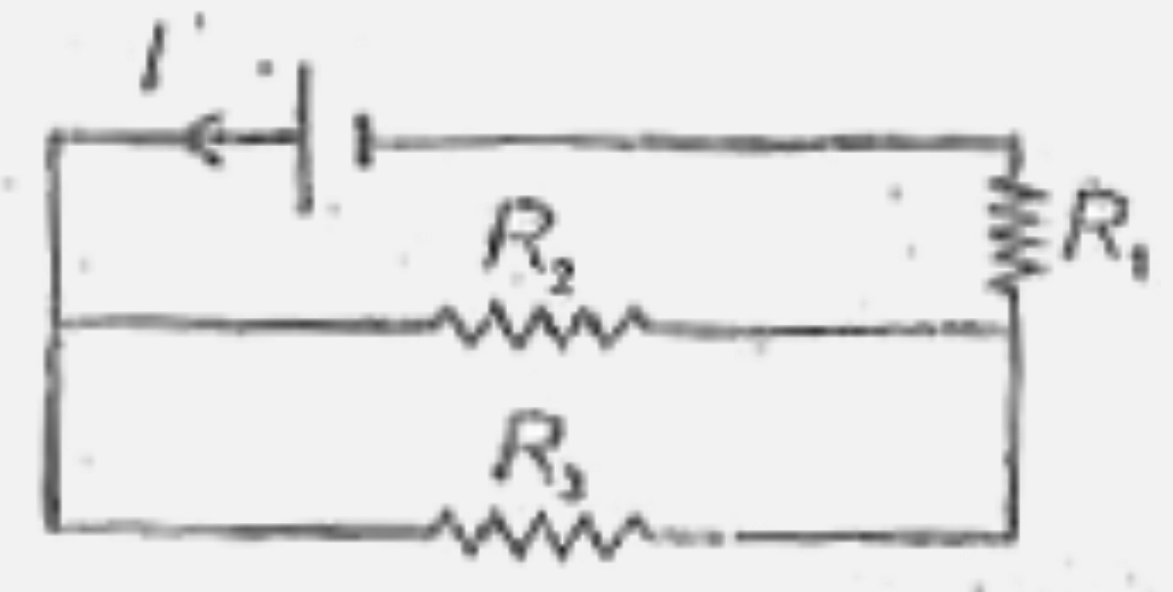
View SolutionRefer to the circuit shown . What will be the total power dissipation in the circuit if P is the power dissipated in R1 ? It is given that R2=4R1 and R3=12R1
View SolutionPower dissipated across the 8Ω in the circuit shown here is 2W. The power dissiated in watt units across the 3Ω is

View SolutionThe power dissipated in the resistance R, in the circuit as shown in the figure, is maximum if R is equal to
View SolutionThe power dissipated in the adjacent circuit is -
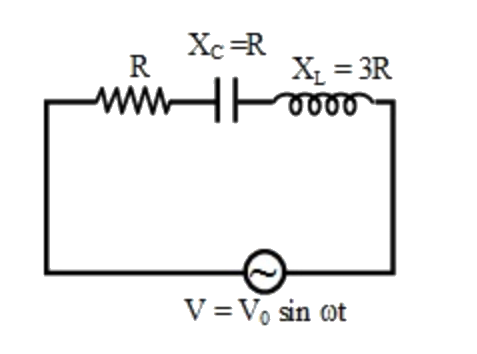
View SolutionIf the power dissipated in the 27Ω resistor in the circuit shown is 108 watt, the potential difference across the 4Ω resistor is
View SolutionFour equal resistance dissipated 5 W of power together when connected in series to a battery of negligible internal resistance . The total power dissipated in these resistance when connected in parallel across the same battery would be .
View Solution

