A student measures the terminal potential difference (V) of a cell (of emf ε and internal resistance r ) as a function fo the current (I) folwing through it . The slope and intercept of the graph between V and I, respectively, equal to
ε and -r
−r and ε
r and −ε
−ε and r
The correct Answer is:B
According to ohm's law
and dVdl=−r
and V=ε if I=0 [As V+IR=ε]
∴ Slope of the graph =-r and intercept =ε
Topper's Solved these Questions
Similar Questions
A student measures the terminal potential difference (V) of a cell (of emf ε and internal resistance r) as a function of the current (I) flowing through it. The slope and intercept of the graph between V and I, then respectively, equal
View SolutionA cell of emf ε and internal resistance r is charged by a current I, then
View SolutionHow are the potential difference (V), current (I) and resistance (R) related ?
View SolutionAccording to this diagram , the potential difference across the terminals is ( internal resistance of cell =r)
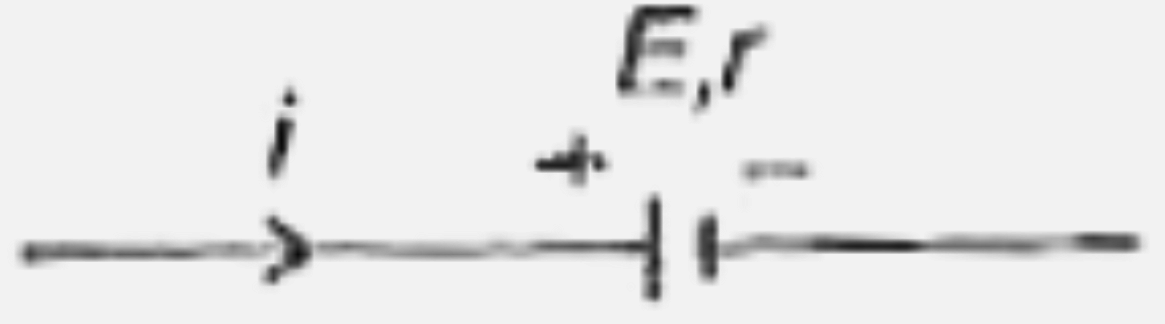 View Solution
View SolutionA cell of emf 'E' and internal resistance 'r' draws a current 'I'. Write the relation between terminal voltage 'V' in terms of E, I and r.
View SolutionA resistor R is connected to a cell of emf e and internal resistance r. Potential difference across the resistor R is found to be V. State the relation between e, V, R and r.
View SolutionCurrent I is being driven through a cell of emf E and internal resistance r as shown in the figure. Choose the following correct statements.
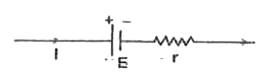 View Solution
View SolutionFor a cell, a graph is plotted between the potential difference V across the terminals of the cell and the current I drawn the cell. The emf and the internal resistance of the cell are E and r, respectively. Then
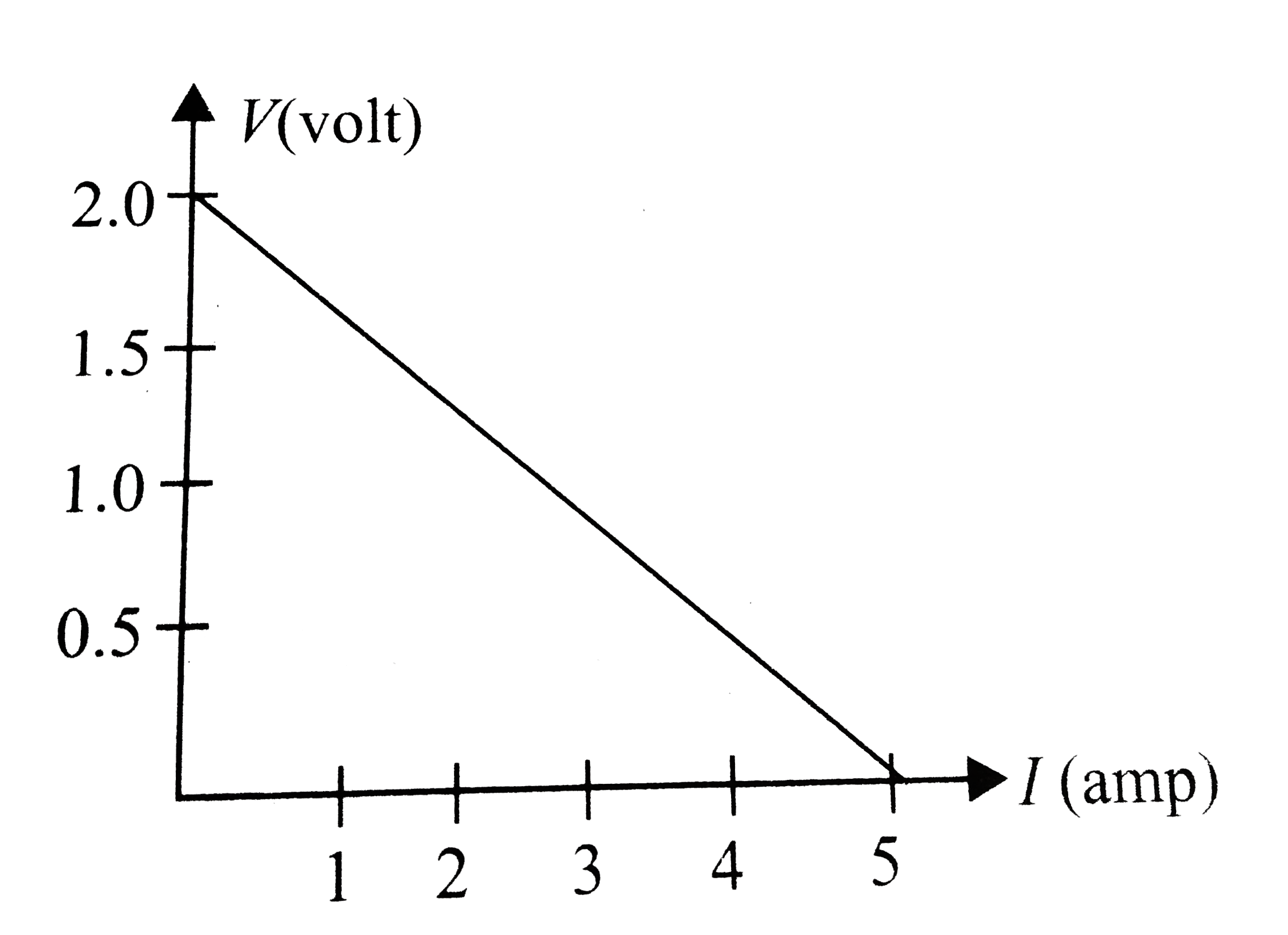 View Solution
View SolutionAssertion: Terminal potential difference of a cell is always less than its emf.
Reason: Potential drop on internal resistance of cell increases terminal potential difference.View SolutionA cell of e.m. E and internal resistance r is connected across a resistancer. The potential difference between the terminals of the cell must be
View Solution
