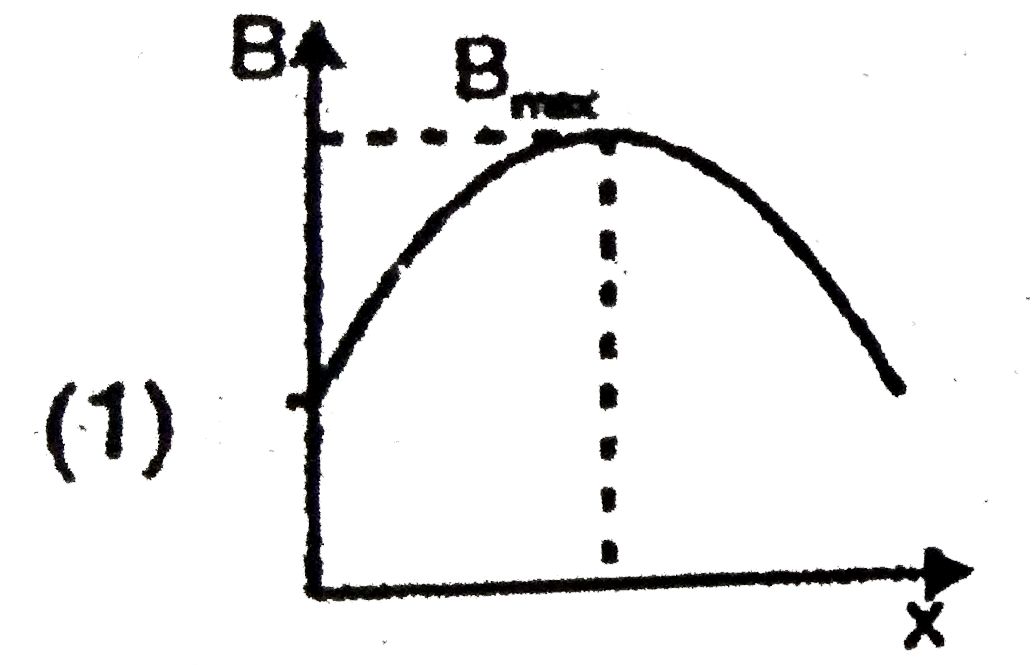
The correct curve between the magnetic induction (B) along the axis of a along solenoid due to current flow i in it and distance x from one end is -


The correct Answer is:A
To solve the problem of determining the correct curve between the magnetic induction (B) along the axis of a long solenoid due to current flow (I) and the distance (x) from one end, we can follow these steps:
Step 1: Understand the Magnetic Field in a Long Solenoid
The magnetic field (B) inside a long solenoid can be expressed as:
B=μ0nI
where:
- μ0 is the permeability of free space,
- n is the number of turns per unit length of the solenoid,
- I is the current flowing through the solenoid.
Step 2: Analyze the Magnetic Field at Different Points
1. At one end of the solenoid (x = 0):
- The magnetic field is given by:
B=μ0nI2
(This is because at the end of the solenoid, the angle θ1 is 90 degrees and θ2 is 0 degrees).
2. At the center of the solenoid:
- The magnetic field is maximum and is given by:
B=μ0nI
(At the center, both angles θ1 and θ2 are close to 0 degrees).
3. At the other end of the solenoid (x = L):
- The magnetic field is again:
B=μ0nI2
(Here, θ1 is 0 degrees and θ2 is 90 degrees).
Step 3: Sketch the Graph
- The magnetic field starts at μ0nI2 at one end (x = 0), increases to μ0nI at the center (x = L/2), and then decreases back to μ0nI2 at the other end (x = L).
- Therefore, the graph of B versus x will be a curve that rises to a maximum at the center and then falls back down, resembling a bell-shaped curve.
Step 4: Identify the Correct Option
- Based on the analysis, the correct curve that represents the relationship between magnetic induction (B) and distance (x) from one end of the solenoid is the one that starts at μ0nI2, reaches a maximum of μ0nI at the center, and returns to μ0nI2 at the other end.
Conclusion
The correct option is the one that shows this bell-shaped curve, indicating that the magnetic field increases from one end to the center and then decreases towards the other end.
---
The magnetic field (B) inside a long solenoid can be expressed as:
B=μ0nI
where:
- μ0 is the permeability of free space,
- n is the number of turns per unit length of the solenoid,
- I is the current flowing through the solenoid.
1. At one end of the solenoid (x = 0):
- The magnetic field is given by:
B=μ0nI2
(This is because at the end of the solenoid, the angle θ1 is 90 degrees and θ2 is 0 degrees).
- The magnetic field is maximum and is given by:
B=μ0nI
(At the center, both angles θ1 and θ2 are close to 0 degrees).
- The magnetic field is again:
B=μ0nI2
(Here, θ1 is 0 degrees and θ2 is 90 degrees).
- The magnetic field starts at μ0nI2 at one end (x = 0), increases to μ0nI at the center (x = L/2), and then decreases back to μ0nI2 at the other end (x = L).
- Therefore, the graph of B versus x will be a curve that rises to a maximum at the center and then falls back down, resembling a bell-shaped curve.
- Based on the analysis, the correct curve that represents the relationship between magnetic induction (B) and distance (x) from one end of the solenoid is the one that starts at μ0nI2, reaches a maximum of μ0nI at the center, and returns to μ0nI2 at the other end.
The correct option is the one that shows this bell-shaped curve, indicating that the magnetic field increases from one end to the center and then decreases towards the other end.
Topper's Solved these Questions
Similar Questions
The magnetic field along the axis of an air cored solenoid is B. The magnetic field energy density is
View SolutionA circular coil of wire of radius 'r' has 'n' turns and carries a current 'I'. The magnetic induction (B) at a point on the axis of the coil at a distance √3r from its centre is
View SolutionA current i ampere flows along the inner conductor of a coaxial cable and returns along the outer conductor fo the cable, then the magnetic induction at any point outside the conductor at a distance r metre from the axis is
View SolutionUsing Ampere's circuital law, obtain an expression for the magnetic field along the axis of a current carrying solenoid of length l and having N number of turns.
View SolutionA magnetic field is established by a circular current i of radius a. Find the magnetic field gradient (i.e. the derivative of the magnetic field induction vector) in the direction of the circular current's axis at a point whose distance from the centre of the turn is x.
View SolutionA slightly divergent beam of charged particles accelerated by a Potential difference V propogates from a point A along the axis of a solenoid. The beam is brought into focus at a distance l from the point A at two successive values of magnetic induction B1andB2. Find the specific charge q/m of the particles.
View SolutionEach of two long parallel wires carries a constant current i along the same direction . The wires are separated by a distance 2I. The magnitude of resultant magnetic induction in the symmetric plane of this system located between the wires at a distance R from each wire will be
View SolutionA proton is projected with a uniform velocity 'v' along the axis of a current carrying solenoid, then
View SolutionFigure shows a straight wire of length a carrying a current I. What is the magnitude of magnetic field induction produced by the current at P, which is lying at a perpendicular distance a from one end of the wire.


View SolutionA wire is bent to form a semi-circle of radius a. the wire rotates about its one end with angular velocity ω.Axis of rotation being perpendicular to plane of the semicircle . In the space , a uniform magnetic field of induction B exists along the axis of rotation as shown . The correct statement is :
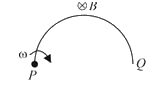
View Solution
