The unit of mutual inductance is-
volt
weber
tesla
henry
The correct Answer is:D
To determine the unit of mutual inductance, we can follow these steps:
Step 1: Understand the Concept of Mutual Inductance
Mutual inductance is the property of a coil (or inductor) that quantifies the induced electromotive force (emf) in one coil due to a change in current in another coil. It is represented by the symbol M.
Step 2: Recall the Definition of Inductance
Inductance (L) is defined as the ratio of the induced emf in a coil to the rate of change of current through it. The formula for inductance is given by:
L=−dΦdt⋅1didt
where Φ is the magnetic flux.
Step 3: Relate Mutual Inductance to Induced EMF
For mutual inductance, the induced emf (E) in one coil due to a change in current in another coil can be expressed as:
E=−Mdidt
where M is the mutual inductance.
Step 4: Determine the Unit of Mutual Inductance
From the equation E=−Mdidt, we can rearrange it to find the unit of mutual inductance:
M=−Edidt
The unit of emf (E) is volts (V), and the unit of current (i) is amperes (A). Therefore, the unit of didt is A/s (amperes per second).
Thus, the unit of mutual inductance can be expressed as:
Unit of M=VoltsAmperes/second=V⋅sA
Step 5: Simplify the Units
Using the relation 1Henry=1V⋅sA, we find that the unit of mutual inductance is indeed Henry (H).
Conclusion
The unit of mutual inductance is Henry (H).
Final Answer
The correct option is D: Henry (H).
---
Mutual inductance is the property of a coil (or inductor) that quantifies the induced electromotive force (emf) in one coil due to a change in current in another coil. It is represented by the symbol M.
Inductance (L) is defined as the ratio of the induced emf in a coil to the rate of change of current through it. The formula for inductance is given by:
L=−dΦdt⋅1didt
where Φ is the magnetic flux.
For mutual inductance, the induced emf (E) in one coil due to a change in current in another coil can be expressed as:
E=−Mdidt
where M is the mutual inductance.
From the equation E=−Mdidt, we can rearrange it to find the unit of mutual inductance:
M=−Edidt
The unit of emf (E) is volts (V), and the unit of current (i) is amperes (A). Therefore, the unit of didt is A/s (amperes per second).
Unit of M=VoltsAmperes/second=V⋅sA
Using the relation 1Henry=1V⋅sA, we find that the unit of mutual inductance is indeed Henry (H).
The unit of mutual inductance is Henry (H).
The correct option is D: Henry (H).
Topper's Solved these Questions
Similar Questions
A current of 10A in the primary of a circuit is reduced to zero at a uniform rate in 10−3 sec. If the coefficient of mutual inductance is 3 henry, what is the induced emf?
View Solutionwrite the unit of self inductance
View SolutionThe coefficient of self inductance and the coefficient of mutual inductance have
View SolutionThe coefficient of mutual inductance when magnetic flux change by 4×10−2Wb and current changes by 0.01A, will be
View SolutionThe coefficient of mutual inductance when magnetic flux change by 2×10−2Wb and current changes by 0.01A, will be
View SolutionThe coefficient of mutual inductance between the primary and secondary of the coil is 5H .A current of 10 A is cut - off in 0.5 s . The induced emf is :
View SolutionA coil of radius r is placed at the centre of the large coil of radius R where R⟩r and coils are in same plane.The coefficient of mutual inductance between the coil is
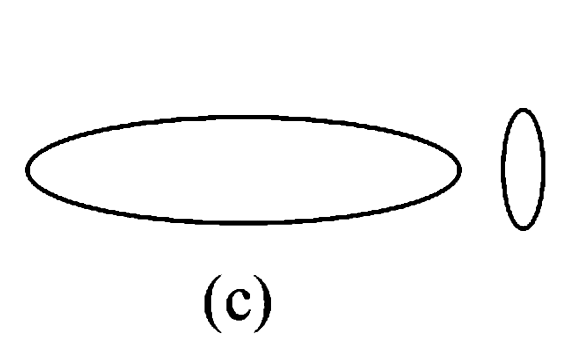
View SolutionTwo circular coils can be arranged in any of the three situation shown in the figure. Their mutual inductance will be
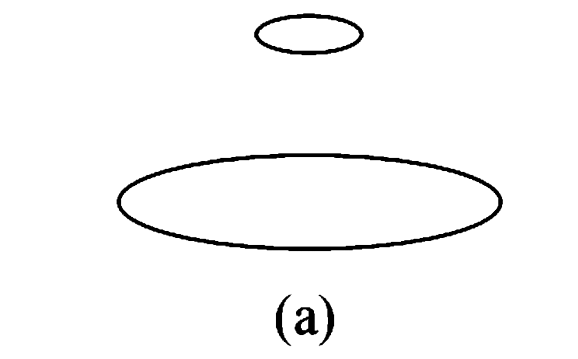 ,
, 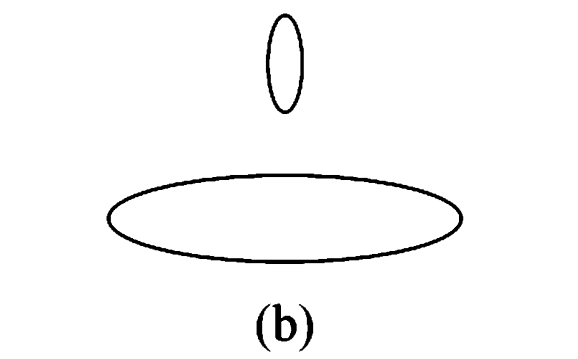 ,
, 
View SolutionTwo circular coils have their centres at the same point. The mutual inductance between them will be maximum when their axes
View SolutionTwo circular coils can be arranged in any of the three situation shown in the figure. Their mutual inductance will be

View Solution
