Let An be the area enclosed by the nth orbit in a hydrogen atom.The grpah of 1n (AnA1) against ln (n)
will pass through the origin
will have certain point lying on a straight line with slope 4
will be a monotonically increasing nonlinear curve
will be a circle
The correct Answer is:A, B
An=πr2=π(r0n2)2
=πr20n4
lnAnA1=ln(n4)=4lnn.

Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Exercise-2 Part-III : Comprehension12videos
ATOMIC PHYSICS
- BOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Exercise -3 part -I JEE (Advanced)86videos
ATOMIC PHYSICS
- BOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Exercise-2 part-II Single and double value integer type12videos
ATOMIC PHYSICS
- BOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - HIGH LEVEL PROBLEMS11videos
ALTERNATING CURRENT
- BOOK - RESONANCE ENGLISHCHAPTER - CAPACITANCEEXERCISE - High Level Problems16videos
CAPACITANCE
Similar Questions
Let An be the area enclosed by the nth orbit in a hydrogen atom. The graph of ln(An/At) against In (n)
View SolutionLet A_(0) be the area enclined by the orbit in a hydrogen atom .The graph of in (A0/A1) againest in(pi)
View SolutionLet A0 be the area enclined by the orbit in a hydrogen atom .The graph of in (A0/A1) against ln(n)
View SolutionThe figure shows a graph between 1n∣∣∣AnA1∣∣∣ and 1n|n|, where An is the area enclosed by the nth orbit in a hydrogen like atom. The correct curve is
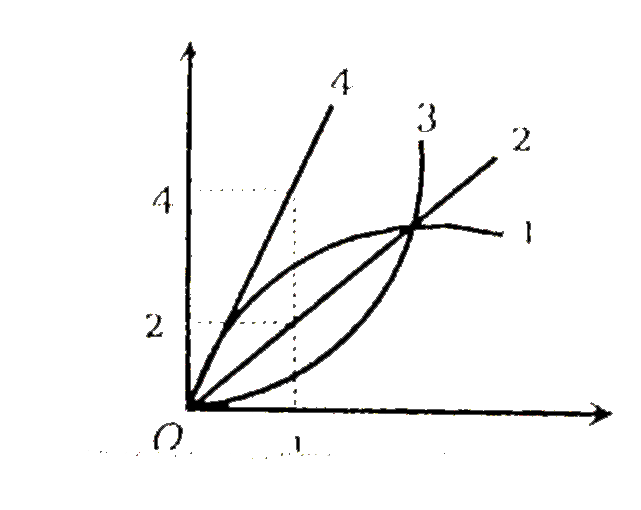 View Solution
View SolutionThe figure shows a graph between 1n∣∣∣AnA1∣∣∣ and 1n|n|, where An is the area enclosed by the nth orbit in a hydrogen like atom. The correct curve is
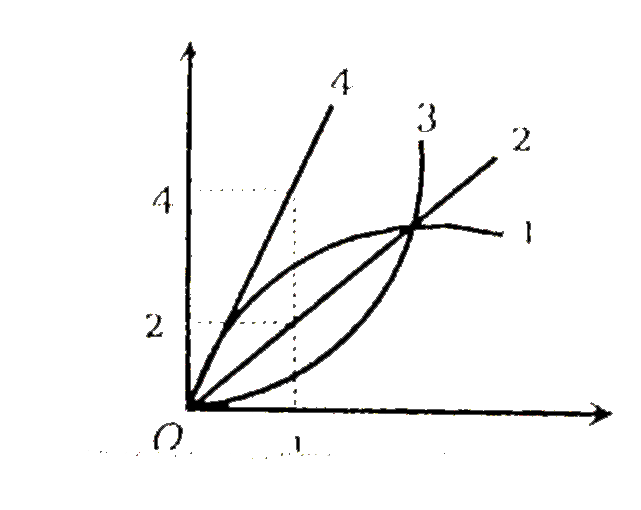 View Solution
View SolutionIf, in a hydrogen atom, radius of nth Bohr orbit is rn frequency of revolution of electron in nth orbit is fn and area enclosed by the nth orbit is An , then which of the pollowing graphs are correct?
View SolutionLet A1,A2,A3,…..,An be squares such that for each n≥1 the length of a side of An equals the length of a diagonal of An+1. If the side of A1 be 20 units then the smallest value of 'n' for which area of An is less than 1.
View SolutionLet an=(1+1n)n. Then for each n∈N
View SolutionIf An is the area bounded by y=x and y=xn,n∈N, then A2.A3…An=
View SolutionLet a1,a2...be positive real numbers in geometric progression. For n, if An,Gn,Hn are respectively the arithmetic mean, geometric mean and harmonic mean of a1,a2,...,an. Then, find an expression for the geometric mean of G1,G2,...,Gn in terms of A1,A2,...,An,H1,H2,...,Hn
View Solution

