The variation of p(x/m) as a function of p when Langmuir's
isotherm valid is :
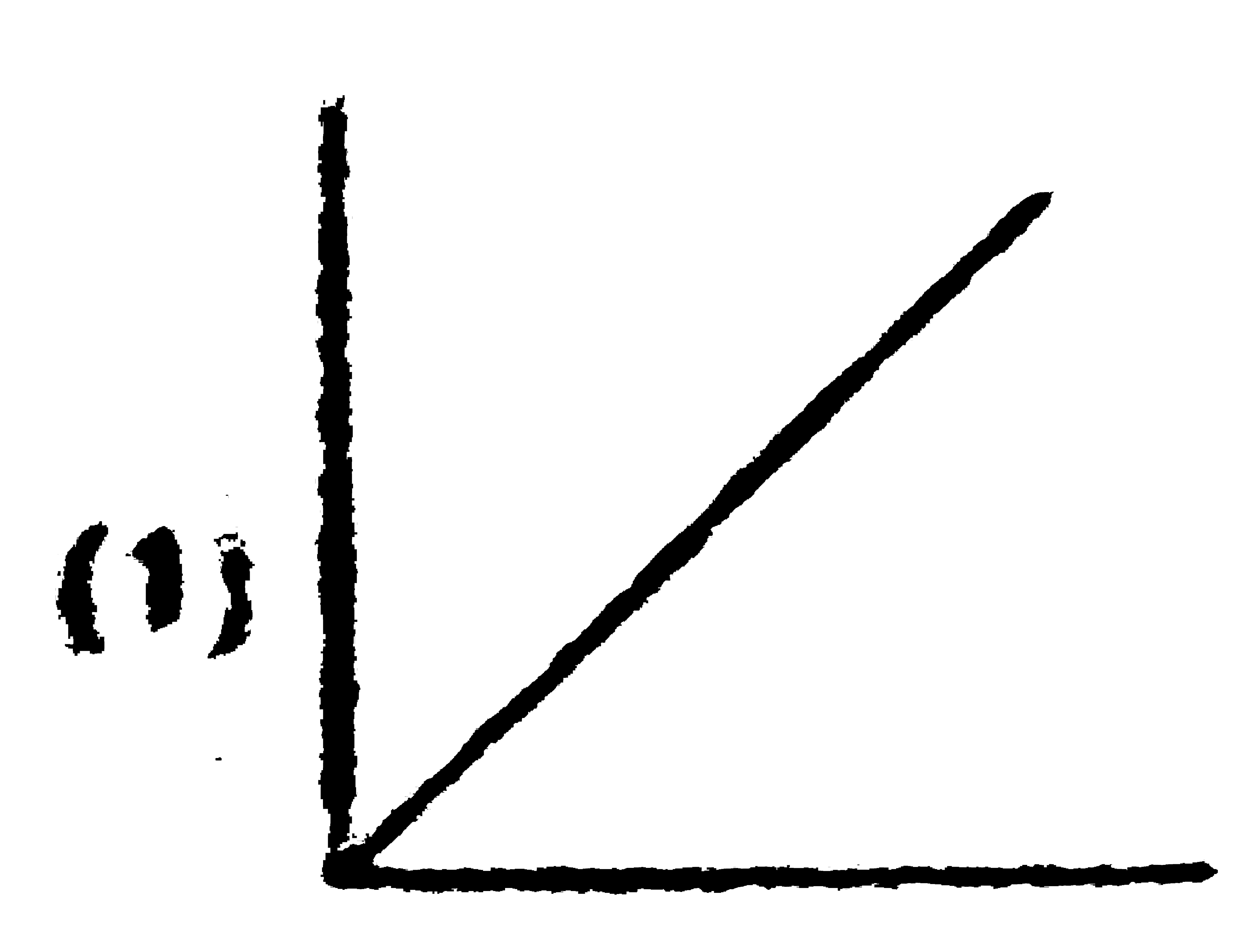
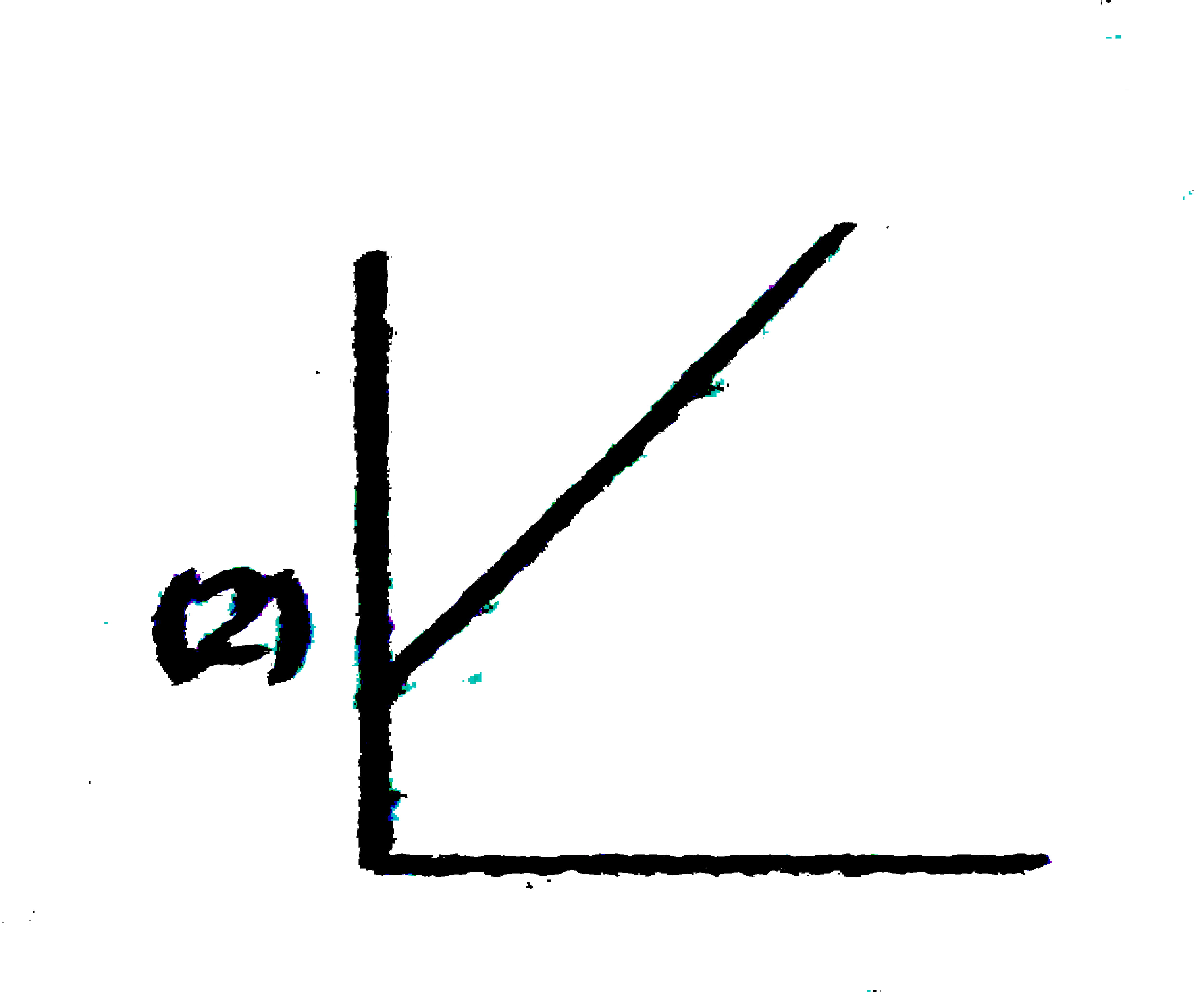


The correct Answer is:2
To solve the question regarding the variation of pxm as a function of p when Langmuir's isotherm is valid, we will follow these steps:
Step 1: Understand Langmuir's Isotherm
Langmuir's adsorption isotherm describes how the amount of gas adsorbed on a solid surface varies with pressure at a constant temperature. The equation is given by:
xm=ap1+bp
where:
- x = amount of gas adsorbed,
- m = mass of the adsorbent,
- p = pressure,
- a and b are constants.
Step 2: Rearrange the Equation
We need to express pxm in terms of p. From the Langmuir equation, we can rearrange it as follows:
xm=ap1+bp
Taking the reciprocal gives:
1xm=1+bpap
Step 3: Express p in Terms of xm
Now, we can express pxm:
pxm=pap1+bp=(1+bp)a
Step 4: Simplify the Expression
This simplifies to:
pxm=1a+bap
Step 5: Identify the Graph Characteristics
The equation pxm=1a+bap is in the form of y=mx+c, where:
- y is pxm,
- x is p,
- m (slope) is ba,
- c (y-intercept) is 1a.
This indicates that the graph is a straight line with a positive slope.
Step 6: Conclusion
The variation of pxm as a function of p when Langmuir's isotherm is valid will yield a straight line graph.
Langmuir's adsorption isotherm describes how the amount of gas adsorbed on a solid surface varies with pressure at a constant temperature. The equation is given by:
- x = amount of gas adsorbed,
- m = mass of the adsorbent,
- p = pressure,
- a and b are constants.
We need to express pxm in terms of p. From the Langmuir equation, we can rearrange it as follows:
Now, we can express pxm:
This simplifies to:
The equation pxm=1a+bap is in the form of y=mx+c, where:
- y is pxm,
- x is p,
- m (slope) is ba,
- c (y-intercept) is 1a.
The variation of pxm as a function of p when Langmuir's isotherm is valid will yield a straight line graph.
Topper's Solved these Questions
- SURFACE CHEMISTRYBook:RESONANCE ENGLISHChapter:SURFACE CHEMISTRYExercise:Solved Examples
Explore 9 Videos
- SURFACE CHEMISTRYBook:RESONANCE ENGLISHChapter:SURFACE CHEMISTRYExercise:Solved Problems
Explore 11 Videos
- STRUCTURAL IDENTIFICATIONBook:RESONANCE ENGLISHChapter:STRUCTURAL IDENTIFICATIONExercise:Advanced level Problems (Part-III)
Explore 12 Videos
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:FST-3
Explore 30 Videos
Similar Questions
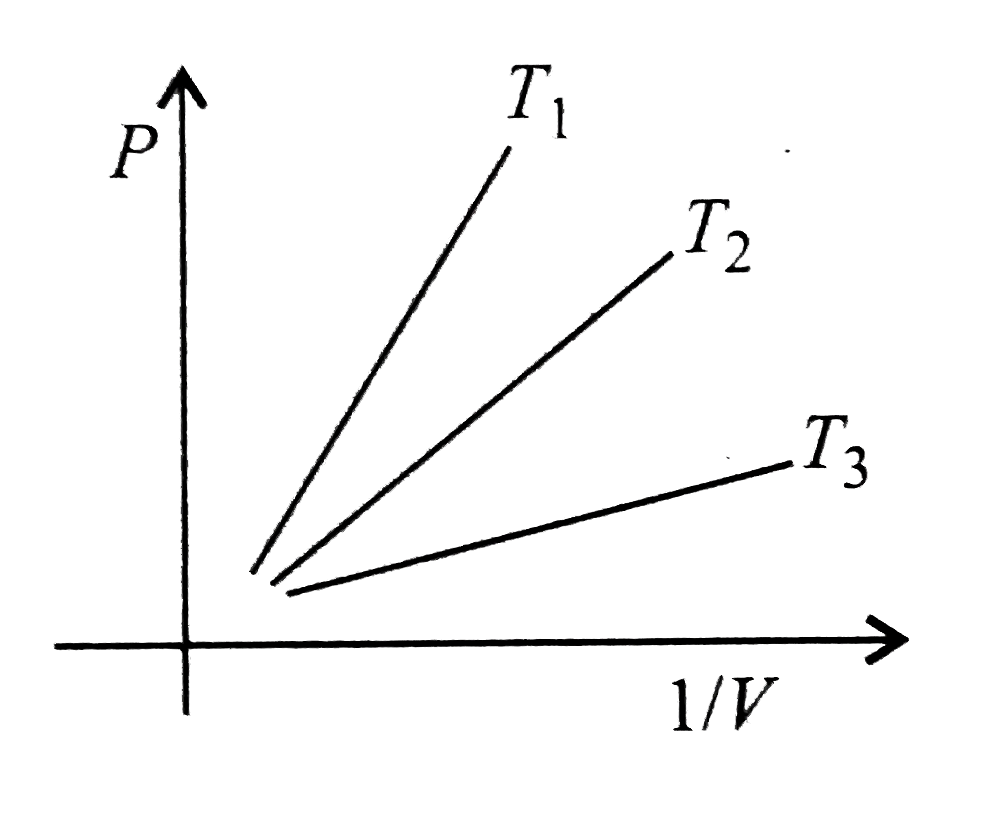
The curve drawn below shows the variations of P as a function of 1/V for a fixed mass and temperature of an ideal gas. It follows from the curve that:
View SolutionThe variation of radial probability density R2 (r) as a function of distance r of the electron from the nucleus for 3p orbital:
(A)(a)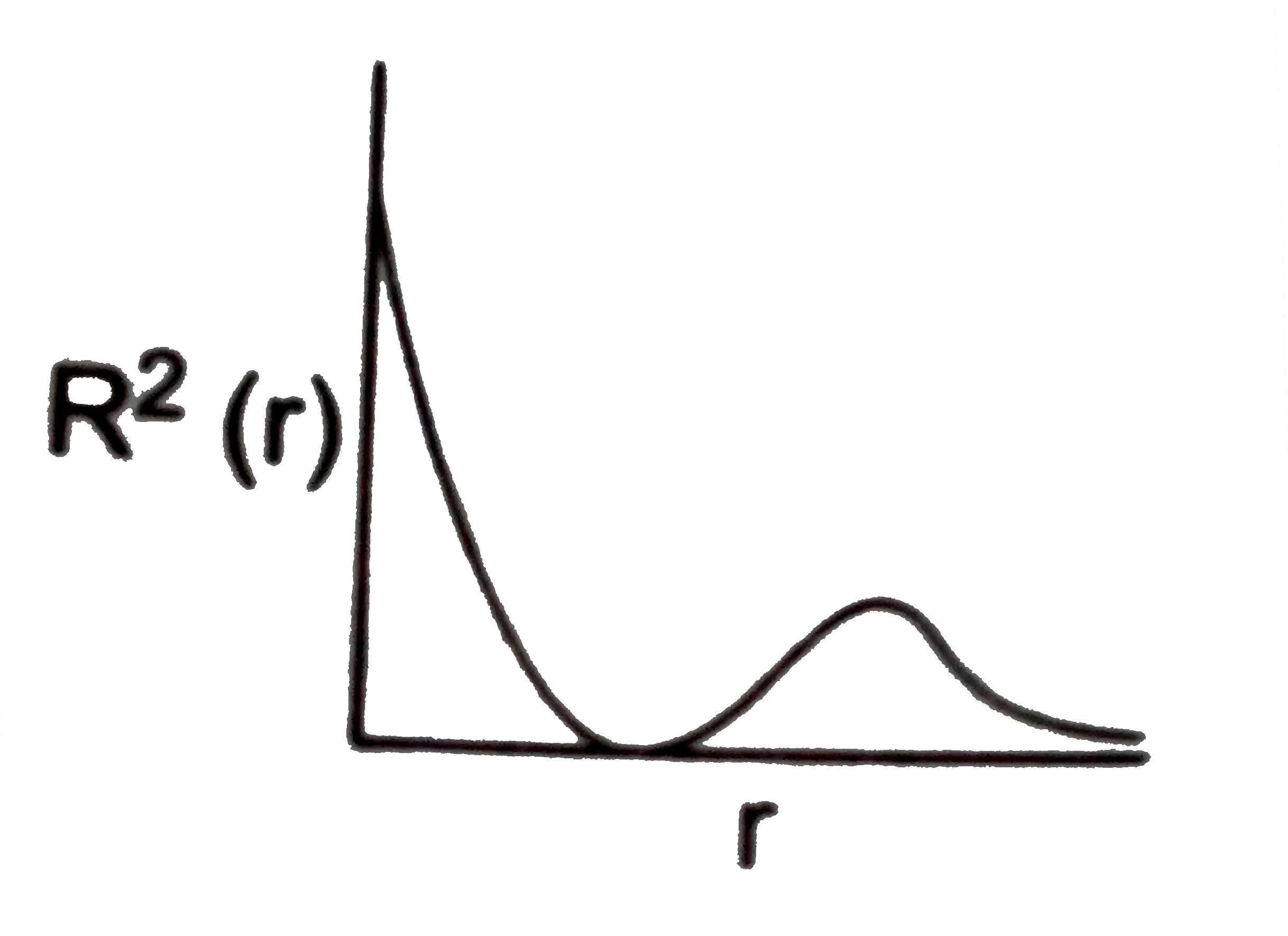
(b) (b)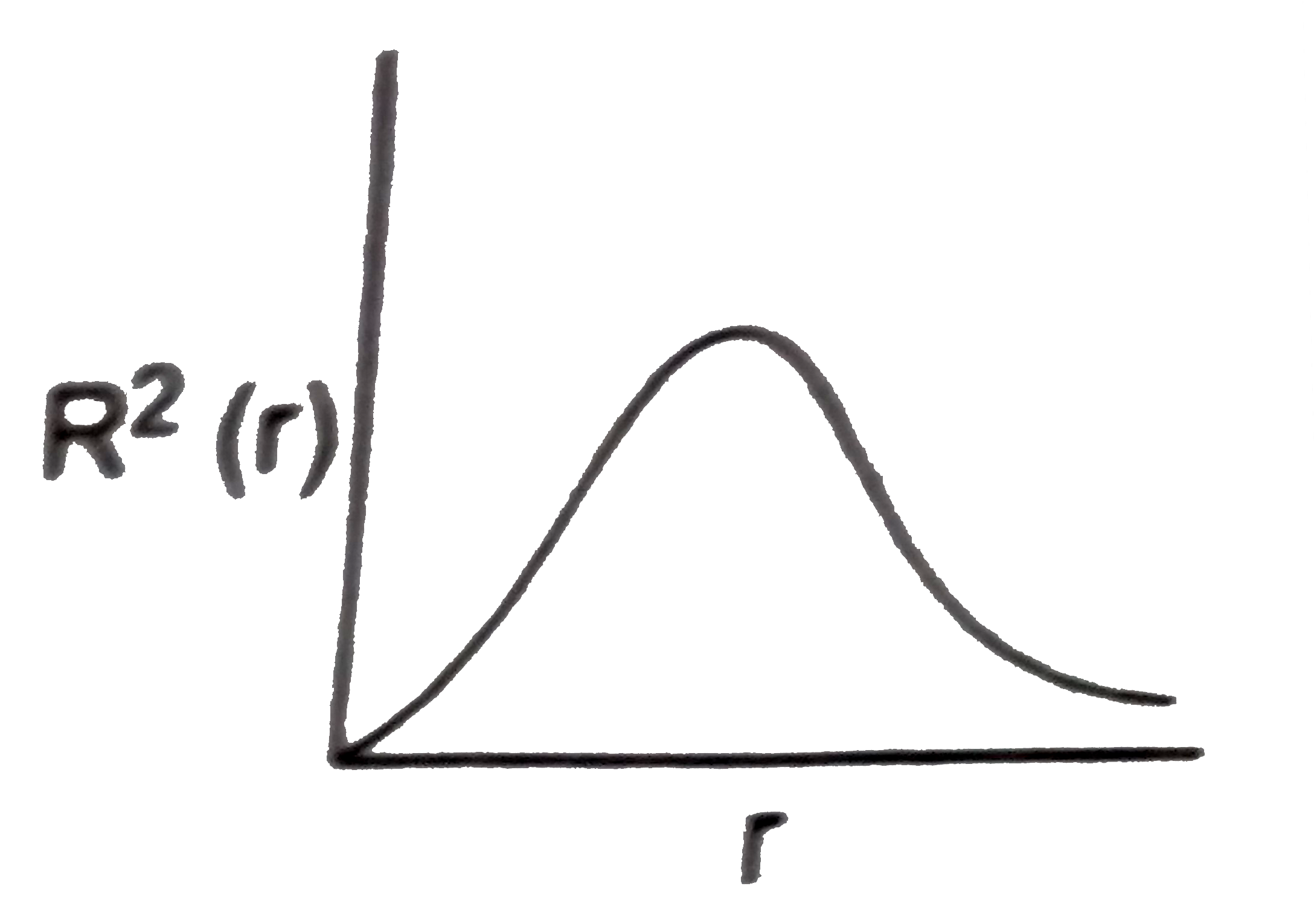
(c)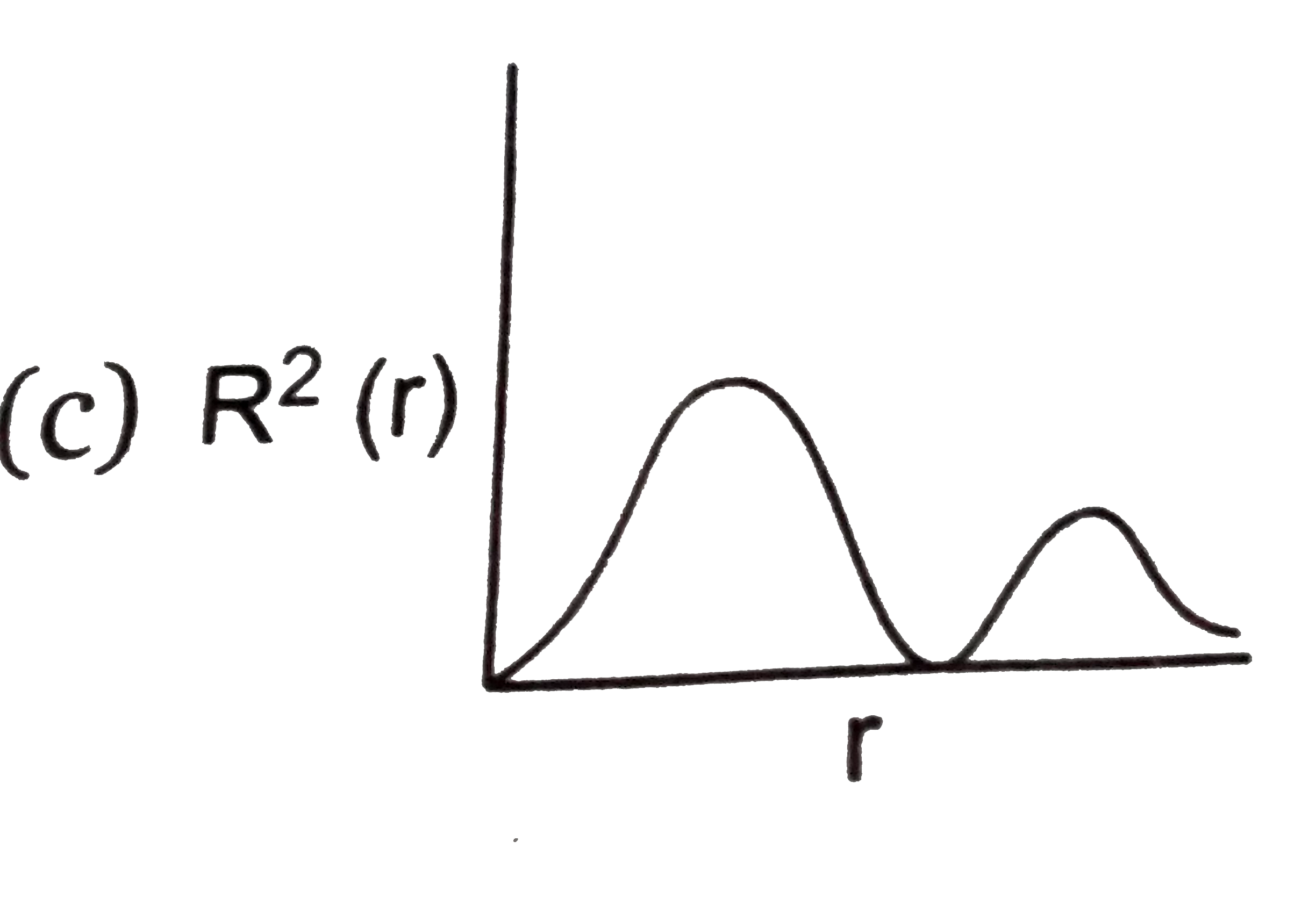
(d)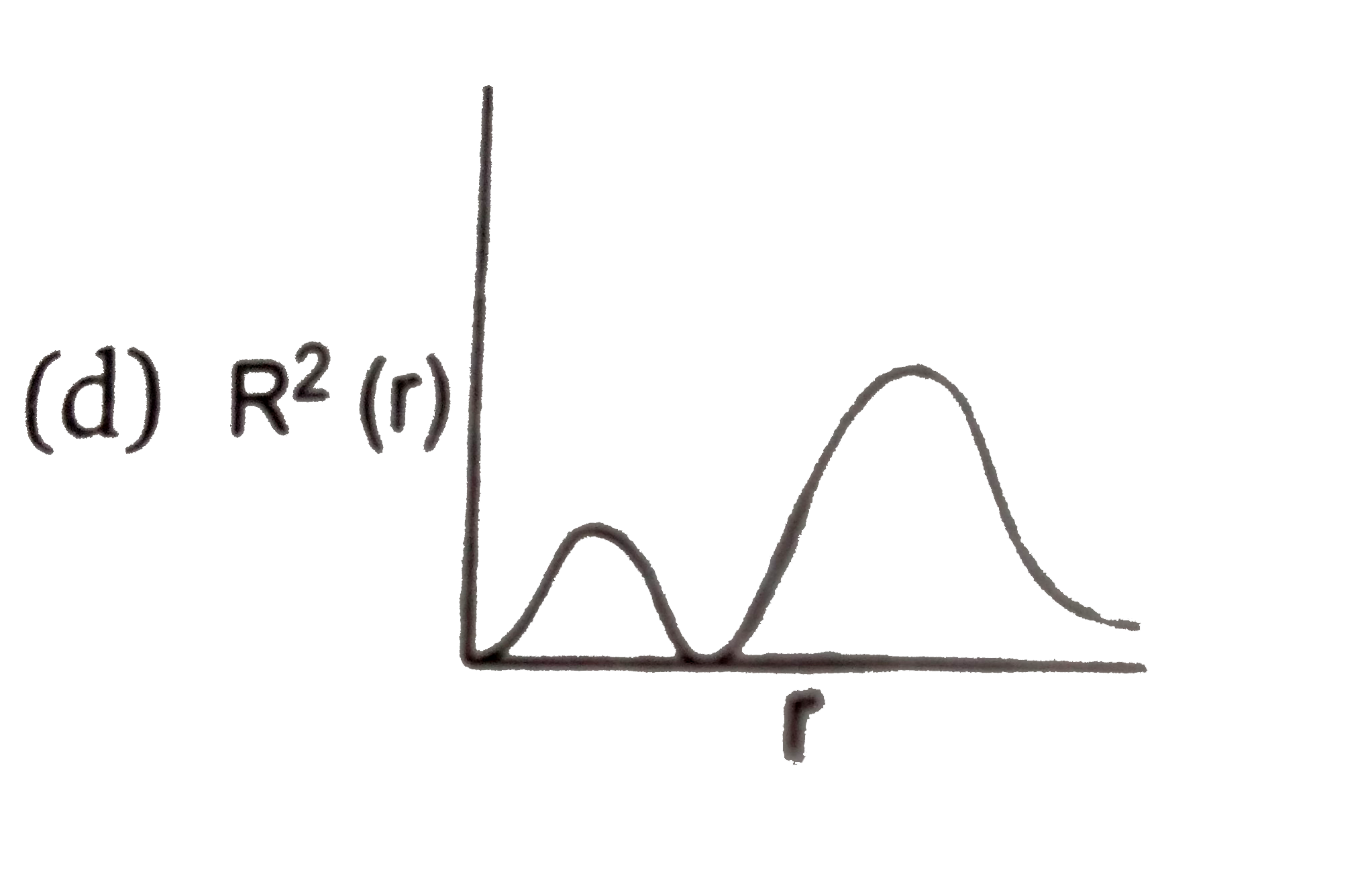
View Solution
Knowledge Check
If p(x) is a polynomial function and p(4)=0, then which statement is true?
Ax+4 is a factor of p(x)Bx-4 is a factor of p(x)CThe greatest power of x in p(x) is 4.Dp(x) is divisible by 4.If p(x) is a polynomial function and p(-1)=3, which statement is true?
AThe remainder when p(x) is divided by x-3 is -1.BThe remainder when p(x) is divided by x+3 is -1.CThe remainder when p(x) is divided by x-1 is 3.DThe remainder when p(x) is divided by x+1 by 3.S(P)=12P+40
D(P)=220−P
The quantity of a product supplied and the quantity of the product demanded in an economic market are functions of the price of the product. The functions above are the estimated supply and demand functions for a certain product. The function S P( ) gives the quantity of the product supplied to the market when the price is P dollars, and the function D P( ) gives the quantity of the product demanded by the market when the price is P dollars.
At what price will the quantity of the product supplied to the market equal the quantity of the product demanded by the market?A$ 90B$120C$133D$155
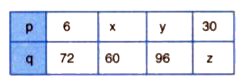
IF p and q are in direct variation of x, y and z in the table given below:
View SolutionConsider the adsorption isotherm given below and interpret the variation in the extent of adsorption (xm) when
a. Temperature increased at constant pressure.
b. Pressure increases at constant temperature.
View SolutionIf x/m is the mass of adsorbate adsorbed per unit mass of adsorbent, P is the pressure of the adsorbate gas ,a and b are constant ,which of the following represent "Langmuir adsorption isotherm"?
View SolutionIn a chemical equilibrium, Kp=Kc is valid if
View SolutionS(P)=12P+40
D(P)=220−P
The quantity of a product supplied and the quantity of the product demanded in an economic market are functions of the price of the product. The functions above are the estimated supply and demand functions for a certain product. The function S P( ) gives the quantity of the product supplied to the market when the price is P dollars, and the function D P( ) gives the quantity of the product demanded by the market when the price is P dollars.
How will the quantity of the product supplied to the market change if the price of the product is increased by $10 ?
View Solution