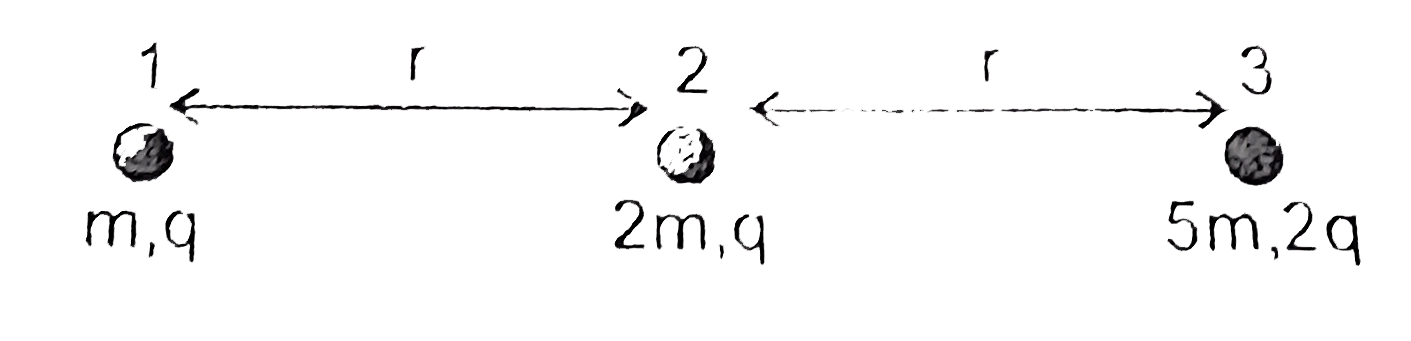
Three particles having charges q,q and 2q have masses m, 2m and 5 m respectively as shown, the three collinear charges are initially released from rest from the positions as shown. (Take K=14π∈0
Q. The maximum kinetic energy of charge of mass 5m is:
a.5Kq24r
b.5Kq22r
c.5Kq23r
d.none of these
The correct Answer is:C
The ratio of velocities of acceleration of mass m, 2m and 5m are −3:−1:1 considering left direction to be negative and right direction to be positive. Hence the distance between m and 2 m at any instant is sae as distance between 2m and 5 m.
As thhe separation between charges becomes very large the loss in potential energy is equal to kq2r+k2q2r+k2q22r=4kq2r and this equals to gain in kinetic for all the three charged particles.
that is 12m×(3x)2+122m×v2+125m×v2=1216m×
v2=4kq2r
∵125mv2=5Kq24r
Similar Questions
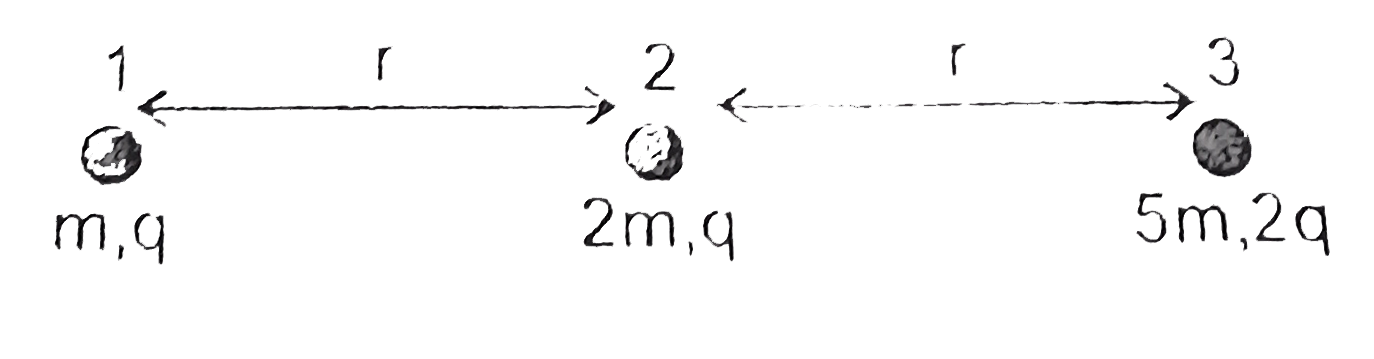
Three particles having charges q,q and 2q have masses m, 2m and 5 m respectively as shown, the three collinear charges are initially released from rest from the positions as shown. (Take K=14π∈0
Q. The ratio of magnitude of acceleration of charge of mass m: charge of mass 2m: charges of mass 5m will be:
View SolutionA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
View SolutionThree charged particles having charges q, -2q & q are placed in a line at points (-a, 0), (0,0) & (a , 0) respectively. The expression for electric potential at P(r, 0 ) for r >> a is
View SolutionThree point charge q1=1μC,q2=−2μC and q3=3μC are placed at (1m,0,0),(0,2m,0) and (0,0,3m) respectively. Find the electric potential at as origin.
View SolutionThree charges -q,+2q, and -q are arranged on a line as shown in fig. Calculate the field at a distance r>>a on the line.
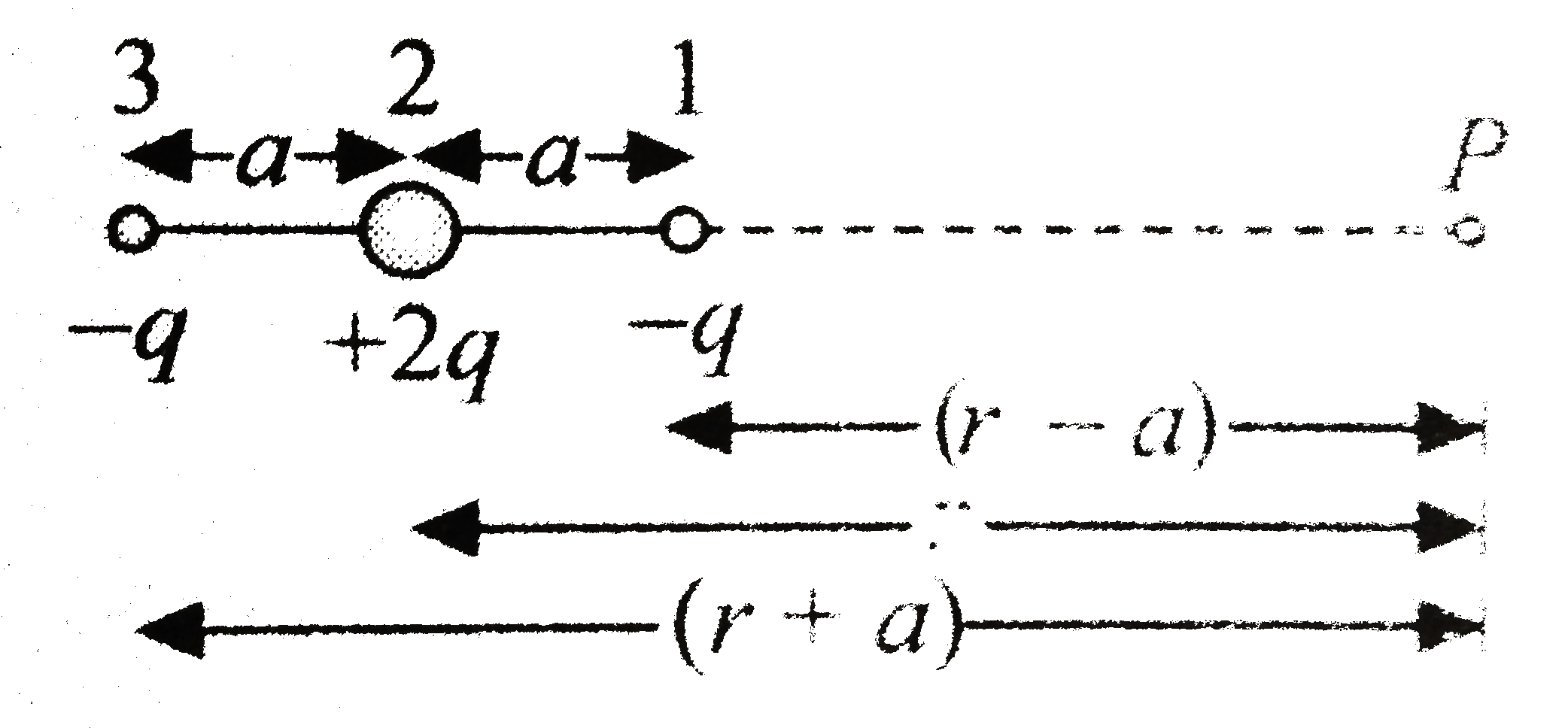
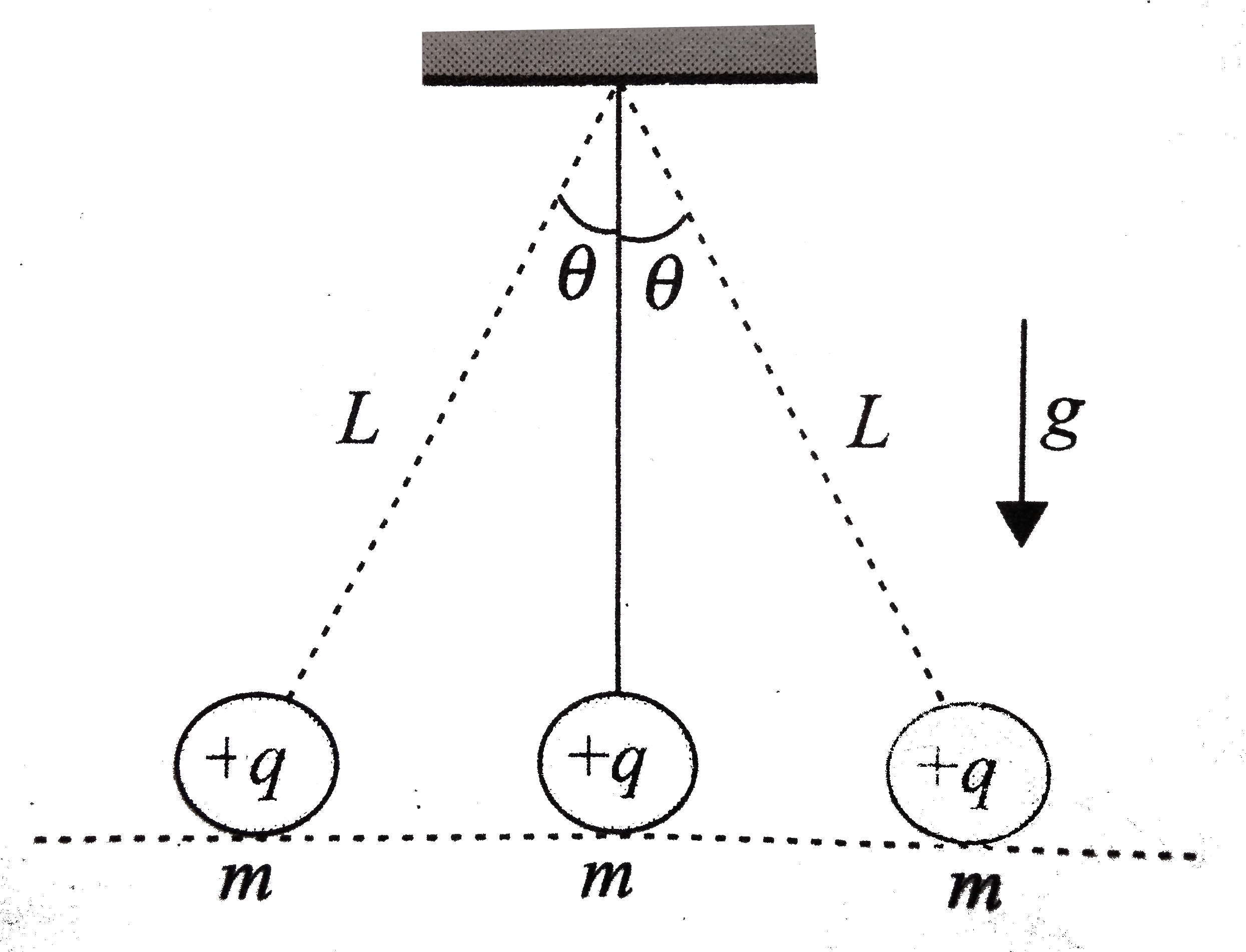
View SolutionThree identical point charges, each of mass m and charge q, hang from three strings as shown in fig. The value of q in term of m, L, and q is
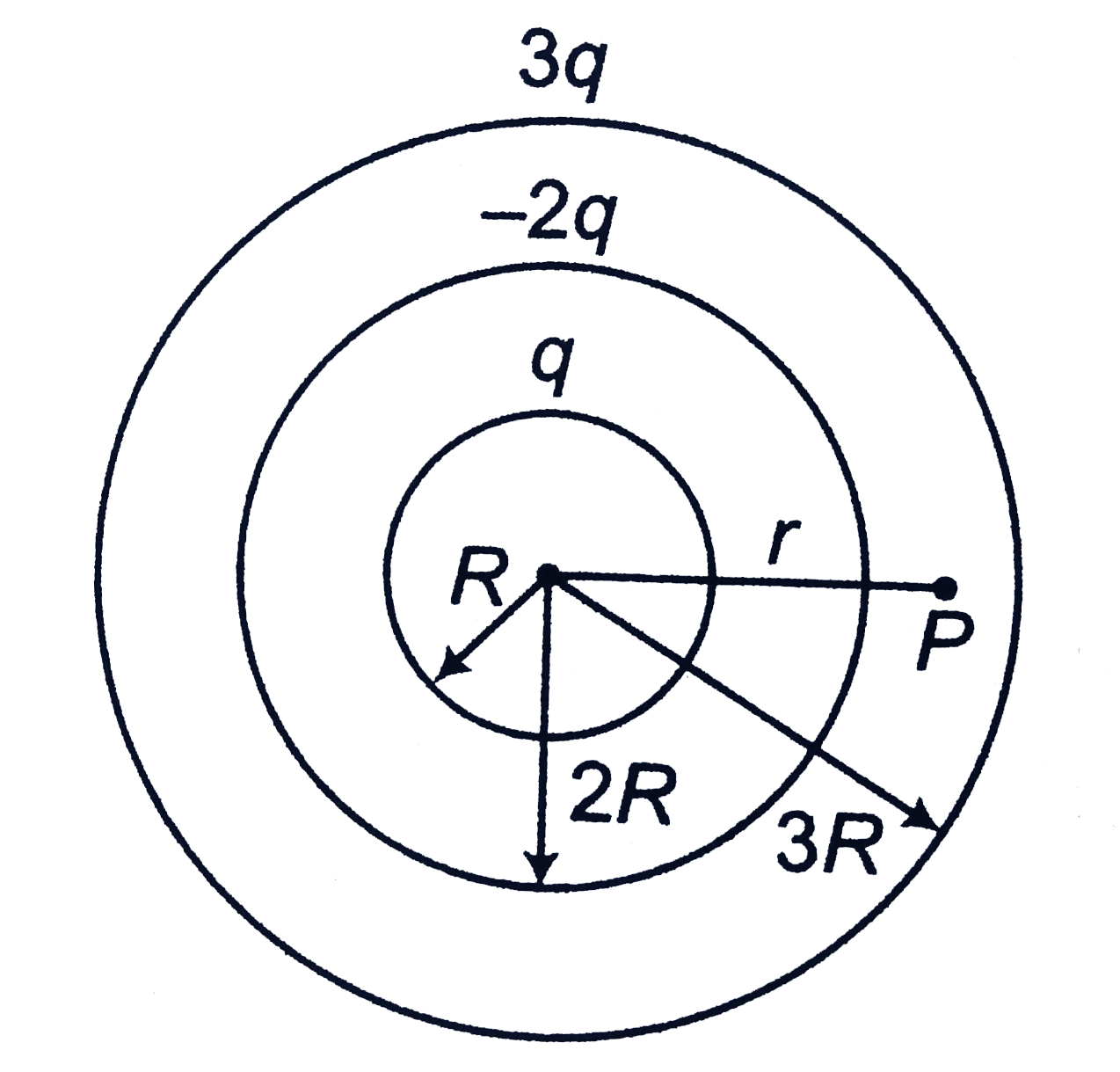
View SolutionThree conducting spherical shells have charges q,−2q and 3q as shown in figure. Find electric Potential at point P as shown in figure.
View SolutionThree particales P,Q and R are placedd as per given Masses of P,Q and R are √3m√3m and m respectively The gravitational force on a fourth particle 'S' of mass m is equal to
 .
.
View SolutionA charged particle of mass m and charge q is released from rest the position (x0,0) in a uniform electric field E0ˆj. The angular momentum of the particle about origin.
View SolutionThe figure shows a region containing a uniform magnetic field B, which is increasing at the rate dBdt The region is gravity free. A disc of mass m and radius R is kept in this magnetic field. Two charged particles having charge q1andq2 and masses m and 2m are embedded to the non-conducting disc on the circumference at diametrically opposite points. The disc is free to translate as well as rotate.

If q1=−qandq2=q , then the initial acceleration of q1 will be
View Solution
