two identical rings of radius R have uniformly distributed charge Q(Q>0) each. Both the rings are fixed and are placed coaxially separated by a distance of R. if a small positive point charge is placed at the mid point and is displaced slightly along the axis then,
it will not perform oscillation
it will perform oscillation but no SHM
it will perform SHM
answer will depend on the magnitude of the charge.
The correct Answer is:A
To solve the problem, we need to analyze the situation of two identical rings with uniformly distributed charge, separated by a distance of R, and a small positive point charge placed at the midpoint between them. We will determine the behavior of the point charge when it is slightly displaced along the axis.
1. Understanding the Setup:
- We have two identical rings, each with radius R and charge Q.
- The distance between the two rings is R.
- A small positive point charge q is placed at the midpoint between the two rings.
2. Electric Field at the Midpoint:
- At the midpoint, the electric fields due to both rings will be equal in magnitude but opposite in direction, resulting in a net electric field of zero.
- Therefore, the point charge experiences no net force when it is exactly at the midpoint.
3. Displacing the Point Charge:
- When the point charge q is displaced slightly by a distance dx along the axis towards one of the rings, the distances from the point charge to each ring will change.
- The distance to the nearer ring will decrease, while the distance to the farther ring will increase.
4. Calculating the Electric Field Change:
- The electric field E due to a ring of charge at a point along its axis is given by:
E=kQ(x2+R2)3/2⋅x
where x is the distance from the center of the ring to the point charge.
- For the displaced position, the electric field from the nearer ring will increase, while the electric field from the farther ring will decrease.
5. Finding the Net Electric Field:
- The net electric field Enet at the displaced position will be:
Enet=Enear−Efar
- As the point charge is displaced, the change in electric field can be analyzed using calculus (differentiation).
6. Condition for Simple Harmonic Motion (SHM):
- For the point charge to undergo SHM, the net force acting on it must be proportional to the displacement from the equilibrium position and directed towards the equilibrium position.
- This implies that the second derivative of the force with respect to displacement should be negative:
dFdx<0
- If this condition is satisfied, the point charge will oscillate about the midpoint.
7. Conclusion:
- After analyzing the conditions for SHM, we find that the displacement x must satisfy certain criteria. If it does not, the point charge will not perform oscillations.
- In this case, based on the analysis, the point charge will not perform oscillations when displaced slightly, leading us to conclude that the correct answer is option A.
- We have two identical rings, each with radius R and charge Q.
- The distance between the two rings is R.
- A small positive point charge q is placed at the midpoint between the two rings.
- At the midpoint, the electric fields due to both rings will be equal in magnitude but opposite in direction, resulting in a net electric field of zero.
- Therefore, the point charge experiences no net force when it is exactly at the midpoint.
- When the point charge q is displaced slightly by a distance dx along the axis towards one of the rings, the distances from the point charge to each ring will change.
- The distance to the nearer ring will decrease, while the distance to the farther ring will increase.
- The electric field E due to a ring of charge at a point along its axis is given by:
E=kQ(x2+R2)3/2⋅x
where x is the distance from the center of the ring to the point charge.
- For the displaced position, the electric field from the nearer ring will increase, while the electric field from the farther ring will decrease.
- The net electric field Enet at the displaced position will be:
Enet=Enear−Efar
- As the point charge is displaced, the change in electric field can be analyzed using calculus (differentiation).
- For the point charge to undergo SHM, the net force acting on it must be proportional to the displacement from the equilibrium position and directed towards the equilibrium position.
- This implies that the second derivative of the force with respect to displacement should be negative:
dFdx<0
- If this condition is satisfied, the point charge will oscillate about the midpoint.
- After analyzing the conditions for SHM, we find that the displacement x must satisfy certain criteria. If it does not, the point charge will not perform oscillations.
- In this case, based on the analysis, the point charge will not perform oscillations when displaced slightly, leading us to conclude that the correct answer is option A.
Similar Questions
Two positive point charges of unequal magnitude are placed at a certain distance apart. A small positive test charge is placed at null point, then
View SolutionTwo points charges +4q and +q are separated by distance r, where should a third point charge Q be placed that the whole system remains in equilibrium
View SolutionIn a free space, a thin rod carrying uniformly distributed negative charge −q is placed symmetrically along the axis of a tin ring of radius R varrying uniformly dostributed charge Q. The mass of the rod is m and length is l=2R. The ring is fixed and the rod is free to move. The rod is displaced slightly along the axis of the ring and then released. Find the period T to the small amplitude oscillations of the rod.
View SolutionA ring of radius R carries a uniformly distributed charge +Q. A point charge −q is placed on the axis of the ring at a distance 2R from the centre of the ring and released from rest. The particle executes a simple harmonic motion along the axis of the ring. State True or False.
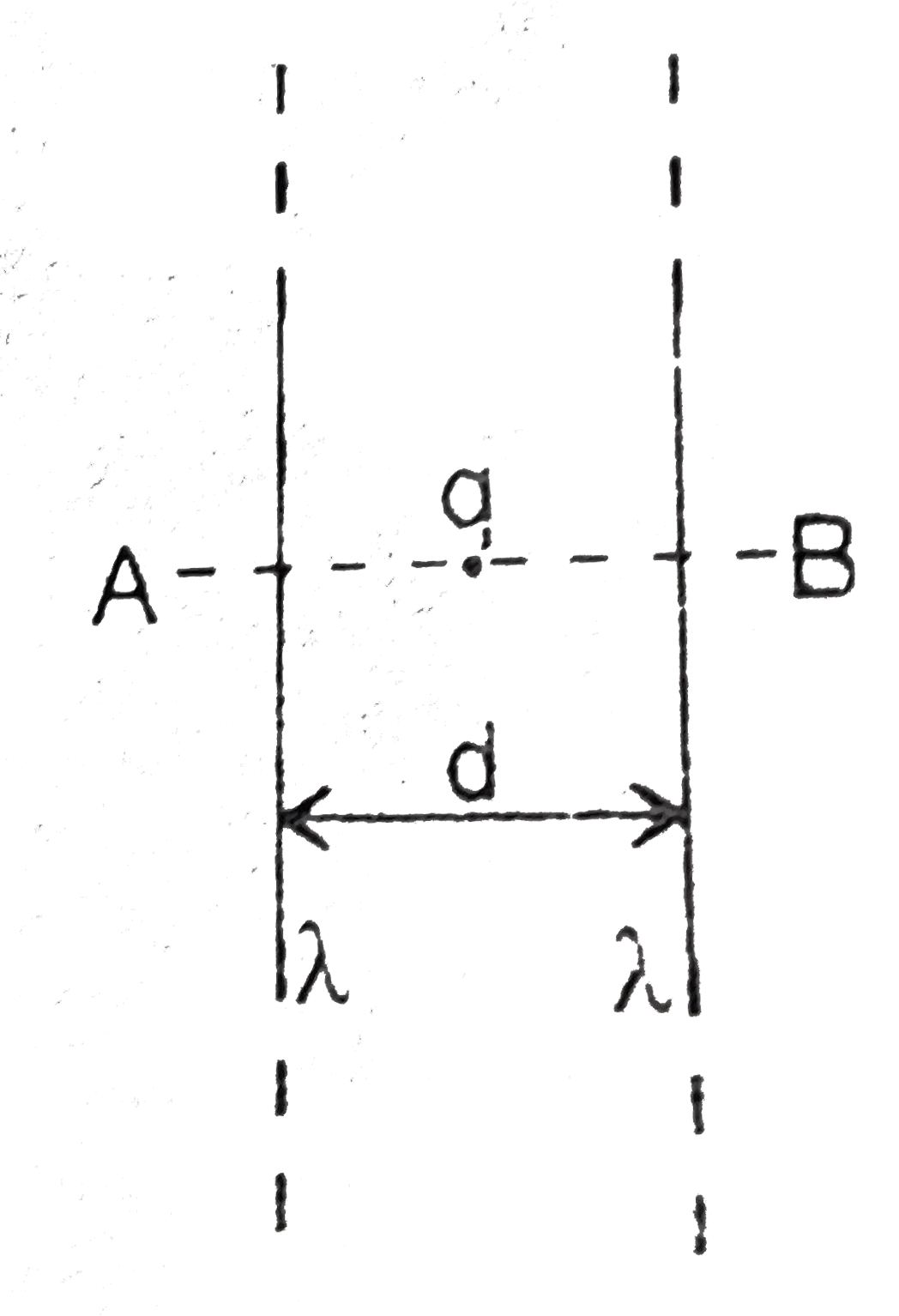
View SolutionTwo infinitely long line charges having charge density λ each are parallel to each other and separated by distance d. A charge particle of mass m and charge q is placed at mid point between them. This charge displaced slightly along a line AB which is perpendicular to the line charges and in the plane of the charges. prove that the motion of the particle will be SHM for small displacement and λq>0 Neglect gravity. Find the time period.
View SolutionTwo point charges Qand−Q/4 placed along the x - axis are separated by a distance r. Take −Q/4 as origin and it is placed at the right of Q. Then the potential is zero.
View SolutionA non conducting ring of radius R has uniformly distributed positive chargeq. A small particle of mass m and charge −q is placed on the axis of the ring at point P and released If R>>x. The particle will undergo oscillations along the axis of symmerty with an angular frequency that is equal to

View SolutionA positive charge Q is uniformly distributed along a circular ring of radius R.a small test charge q is placed at the centre of the ring.

View SolutionCalculate potential on the axis of a ring due to charge Q uniformly distributed along the ring of radius R.
View SolutionA positive charge Q is uniformly distributed along a circular ring of radius R.a small test charge q is placed at the centre of the ring .The

View Solution
