A 1.5 kg block is initially at rest on a horizontal frictionless surface when a horizontal force in the positive direction of an axis is applied to the block. The force is given by , where x is in meters and the initial position of the block is the maximum kinetic energy of the block is in between ad m find the value of .
To solve the problem, we need to determine the maximum kinetic energy of the block when subjected to the given force. The force acting on the block is →F=(1−x2)^iN.
1. Understanding the Force: The force acting on the block is a function of position x. It is given as F(x)=1−x2. This force will do work on the block as it moves from x=0 to x=2.
2. Work Done by the Force: The work done W by the force as the block moves from position x=0 to x=2 can be calculated using the integral of the force over the distance:
W=∫20F(x)dx=∫20(1−x2)dx
3. Calculating the Integral:
W=∫20(1−x2)dx=(x−x33)20
=(2−233)−(0−0)=2−83=2−2.67=−0.67J
4. Kinetic Energy: According to the work-energy theorem, the work done on the block is equal to the change in kinetic energy. Since the block starts from rest, the initial kinetic energy is 0:
W=ΔKE=KEfinal−KEinitial=KEfinal−0
Therefore, the maximum kinetic energy KEmax is equal to the work done:
KEmax=W=−23J
5. Finding the Value of n: The problem states that the maximum kinetic energy is given by 2nJ. Setting the two expressions for kinetic energy equal gives:
−23=2n
Cross-multiplying gives:
−2n=6⟹n=−3
Final Answer:
The value of n is −3.
W=∫20F(x)dx=∫20(1−x2)dx
W=∫20(1−x2)dx=(x−x33)20
=(2−233)−(0−0)=2−83=2−2.67=−0.67J
W=ΔKE=KEfinal−KEinitial=KEfinal−0
Therefore, the maximum kinetic energy KEmax is equal to the work done:
KEmax=W=−23J
−23=2n
Cross-multiplying gives:
−2n=6⟹n=−3
The value of n is −3.
Similar Questions
A 1.5−kg block is initially at rest on a horizontal frictionless surface when a horizontal force in the positive direction of x-axis is applied to the block. The force is given by →F=(4−x2)→iN, where x is in meter and the initial position of the block is x=0.
The maximum kinetic energy of the block between x=0 and x=2.0m is
A.2.33 J B.8.67 J C.5.33 J D.6.67 J
View SolutionA block of mass 2 kg rests on a horizontal surface. If a horizontal force of 5 N is applied on the block, the frictional force on it is (take,uk=0.4,μs=0.5)
View Solution
Knowledge Check
A block of mass 2kg initially at rest moves under the action of an applied horizontal force of 6 N on a rough horizontal surface. The coefficient of friction between the block and surface is 0.1. the work done by friction in 10 s is
A200JB−200JC600 JD−600J
A block of mass 2kg si kept at rest at x=0, on a rough horizontal surface with coefficient of a rough horizontal surface with coefficient of friction 0.2. A position dependent horizontal force given by F=x2+2x+5 (where x is in meter and F is in Newton), starts acting on the block at x=0. The kenetic energy of block at x=3 is :
View SolutionIn a horizontal spring-block system force constant of spring is k = 16N/m, mass of the block is 1 kg. Maximum kinetic energy of the block is 8J. Then
View SolutionBlocks are in contact on a frictionless table. A horizontal force F=3N is applied to one block as shown. The force exerted by the smaller block m2 on block m1 is :
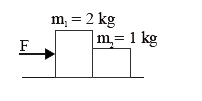
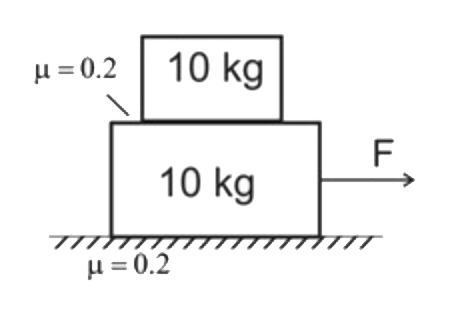
View SolutionInitially, both the blocks are at rest on horizontal surface as shown in the figure. Find the minimum value of force F in (N) so that sliding starts between the blocks (g=10ms−2)
View SolutionTwo blocks of masses 2 kg and 1 kg are in contact with each other on a frictionless table. When a horizontal force of 3.0 N is applied to the block of mass 2 kg the value of the force of contact between the two blocks is:
View SolutionTwo blocks of masses 2 kg and 1 kg are in contact with each other on a frictionless table. When a horizontal force of 3.0 N is applied to the block of mass 2 kg the value of the force of contact between the two blocks is:
View SolutionA block is kept on a rough horizontal surface. A variable horizontal force is acting on the block as shown in the figure. At t=0, block is at rest. Kinectic energy of block at t=5sec will be (g=10m/s2)
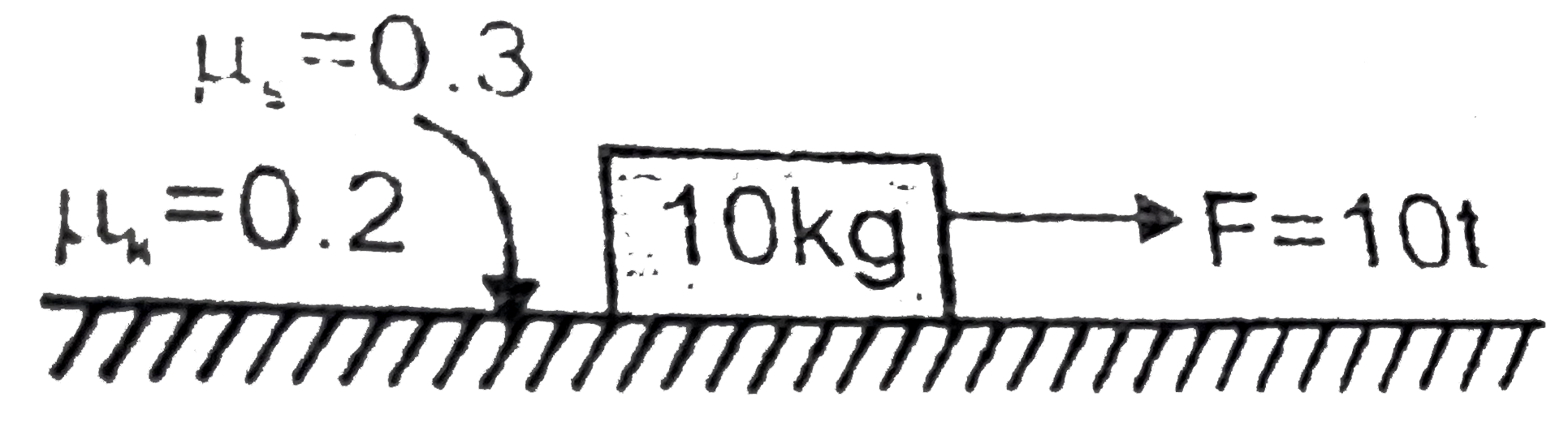
View Solution
