A block of mass 2 kg rests on a horizontal surface. If a horizontal force of 5 N is applied on the block, the frictional force on it is (take,uk=0.4,μs=0.5)
(a)5N
(b)10N
(c)8N
(d)zero
The correct Answer is:3
To solve the problem step by step, we will analyze the forces acting on the block and determine the frictional force.
Step 1: Identify the given data
- Mass of the block, m=2kg
- Applied horizontal force, F=5N
- Coefficient of kinetic friction, μk=0.4
- Coefficient of static friction, μs=0.5
Step 2: Calculate the weight of the block
The weight W of the block can be calculated using the formula:
W=m⋅g
where g (acceleration due to gravity) is approximately 10m/s2.
W=2kg⋅10m/s2=20N
Step 3: Determine the normal force
Since the block is resting on a horizontal surface, the normal force N acting on the block is equal to its weight:
N=W=20N
Step 4: Calculate the maximum static friction force
The maximum static friction force Fs can be calculated using the coefficient of static friction:
Fs=μs⋅N
Substituting the known values:
Fs=0.5⋅20N=10N
Step 5: Compare the applied force with the maximum static friction force
The applied force F is 5N, which is less than the maximum static friction force Fs=10N. This means that the block will not move, and the frictional force will equal the applied force to prevent motion.
Step 6: Determine the frictional force
Since the applied force is less than the maximum static friction force, the frictional force Ff will be equal to the applied force:
Ff=F=5N
Final Answer
The frictional force acting on the block is 5N.
---
- Mass of the block, m=2kg
- Applied horizontal force, F=5N
- Coefficient of kinetic friction, μk=0.4
- Coefficient of static friction, μs=0.5
The weight W of the block can be calculated using the formula:
W=m⋅g
where g (acceleration due to gravity) is approximately 10m/s2.
W=2kg⋅10m/s2=20N
Since the block is resting on a horizontal surface, the normal force N acting on the block is equal to its weight:
N=W=20N
The maximum static friction force Fs can be calculated using the coefficient of static friction:
Fs=μs⋅N
Substituting the known values:
Fs=0.5⋅20N=10N
The applied force F is 5N, which is less than the maximum static friction force Fs=10N. This means that the block will not move, and the frictional force will equal the applied force to prevent motion.
Since the applied force is less than the maximum static friction force, the frictional force Ff will be equal to the applied force:
Ff=F=5N
The frictional force acting on the block is 5N.
Topper's Solved these Questions
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - EFFICIENT
50 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE Advanced (archive)
14 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)
55 Videos
Similar Questions
A block of mass 20kg is placed on a rough horizontal plane and a horizontal force of 12N is applied. If coefficient of friction is 0.1 the frictional force acting on it is,
View SolutionA block of unknown mass is at rest on a rough, horizontal surface. A horizontal force F is applied to the block. The graph in the figure shows the acceleration of the block with respect to the applied force. The mass of the block is

View SolutionA block of mass 5kg rests on a rough horizontal surface. It is found that a force of 10N is required to make the block just move However , once the motion begains, a force of only 8N is enough to maintain the motion find the coefficient of kinetic and static friction between the block and the horizontal surface

View SolutionA block of mass 5kg rests on a rough horizontal surface. It is found that a force of 10N is required to make the block just move However , once the motion begains, a force of only 8N is enough to maintain the motion find the coefficient of kinetic and static friction between the block and the horizontal surface

View SolutionA block of mass 1 kg in kept on a rough horizontal surface with μs=0.1 . A force of 0.5 N is applied as shown in the figure. What is the frictional force applied by ground on the block?
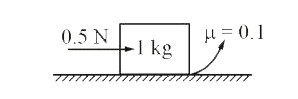
View SolutionA block of mass 10kg is placed on a horizontal surface as shown in the figure and a force F=100N is applied on the block as shown, in the figure. The block is at rest with respect to ground. If the contact force between block and ground is 25n (in Newton) then value of n is : (Takeg=10m/s2)

View SolutionA block of mass 4 kg is kept on a rough horizontal surface. The coefficient of static friction is 0.8. If a forace of 19 N is applied on the block parallel to the floor, then the force of friction between the block and floor is
View SolutionA block of mass 20 kg is on a horizontal plane of a coefficient of friction 0.5. by applying 6.0 newton force on it, frictional force will be (g=10m/s2).
View SolutionSuppose a block of mass 1kg is placed over a rought surface and a horizontal force F is applied on the block as shown in figure. Now let as see what are the values of force of friction f and acceleration of the block a if the force F is gradually increased. Given that μs=0.5,μk=0.4andg=10m/s2

View SolutionA block of mass 5 kg is kept on a rough horizontal surface. The coefficient of friction for the contact force block and surface are μs=0⋅1andμk=0⋅9 respectively . A horizontal force F given by F 0⋅5t is applied at t = 0 . Here t represent time in seconds . Determine the force of friction and acceleration of the block at
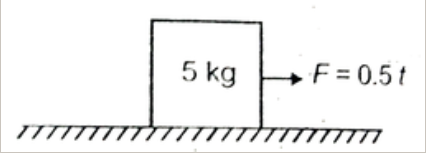
(i) t = 1s (ii) t= 10 s (iii) t = 12 s
View Solution
