A wave pulse is generated at the bottom of a uniform string (of mass m and length l) Suspended from ceiling and supporting a block (of mass m) as shown. 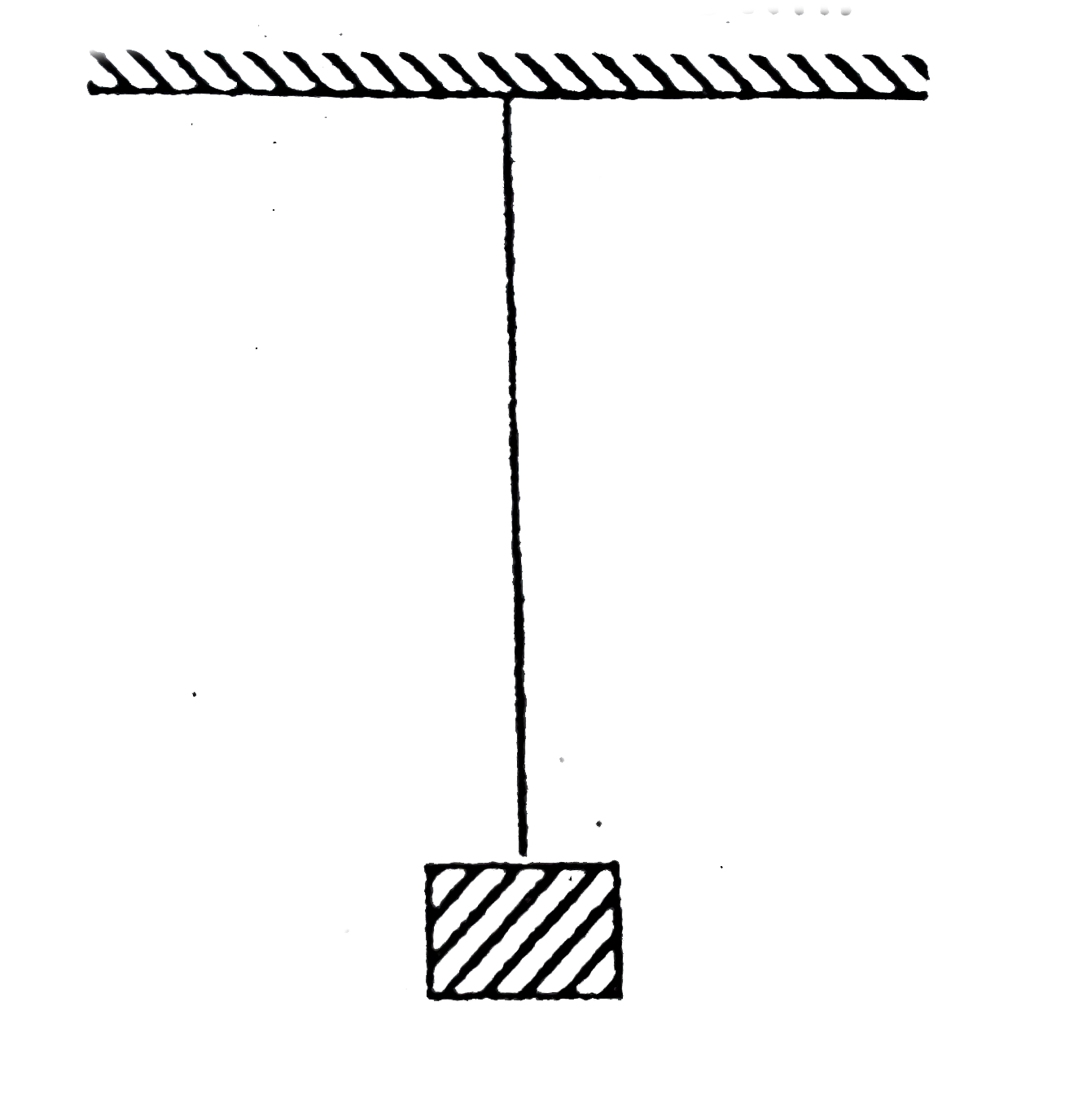
Acceleration of the wave pulse is g2
Time taken by the wave pulse to travel from botom to ceiling is ((√2+1).2)√lg
Speed of the wave at bottom of string is √gl
Speed of the wave as it is just about to strike the ceiling is√2gl
The correct Answer is:A, C, D
At a distance x from the bottom,
V=√Tμ=√mg+mgxlml=√g(l+x)
⇒a=V.dVdx=g2
Time of motion =g2lVaverage=2l√gl+√2gl
=2(√2+1)√lg
Topper's Solved these Questions
Similar Questions
A uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is

View SolutionA particle of mass m is attached to an end of a uniform rod of mass M = 2m and length l1 which is suspended through its mid point by an inextensible string as shown initially the rod is in horizontal position and at rest. The system is released from this position Just after the release
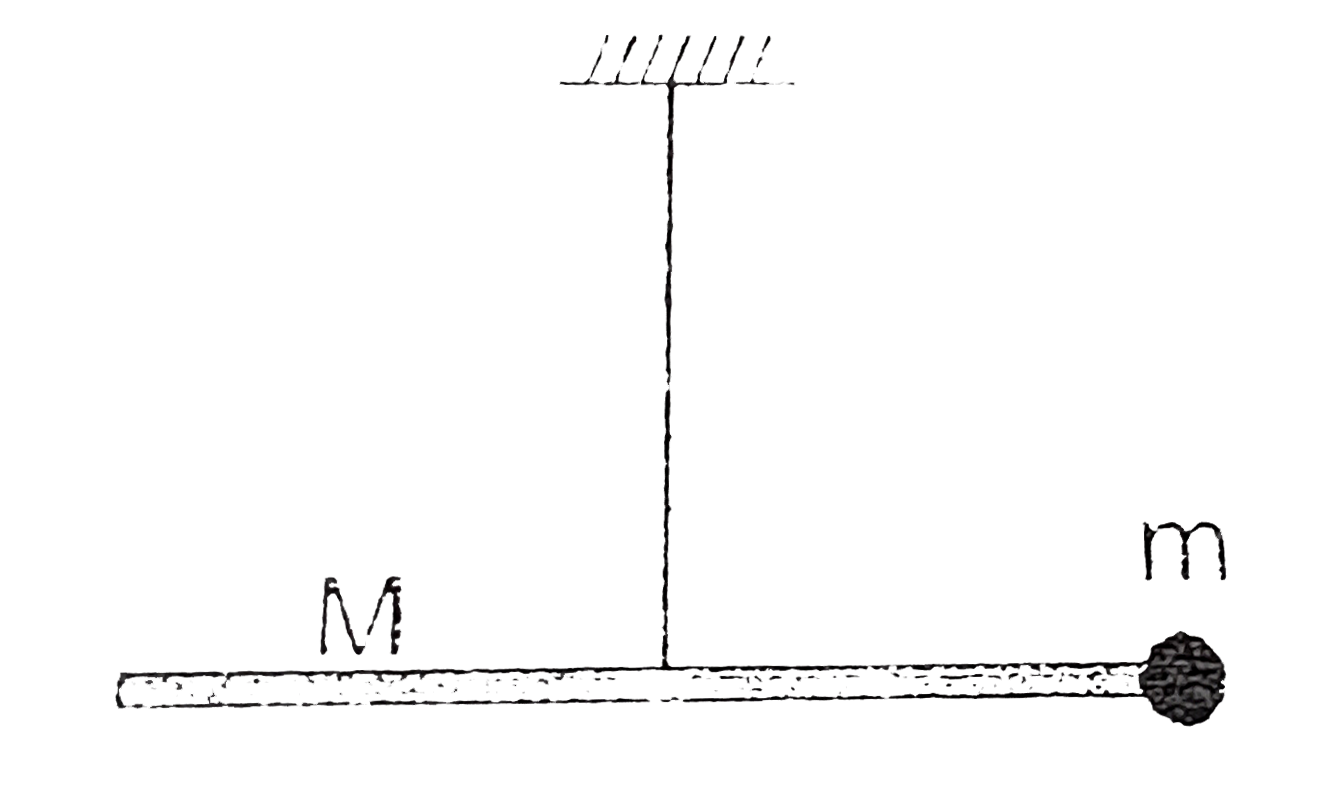
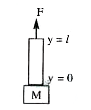
View SolutionA vertical force of magnitude Facts at the top of a string of mass 'm' and length 'l'. A body of mass M hangs at the bottom of the string.
View SolutionA block M hangs vertically at the bottom end of a uniform rope of constant mass per unit length. The top end of the rope is attached to a fixed rigid support at O. A transverse wave pulse (Pulse 1) of wavelength λ0 is produced at point O on the rope. The pulse takes time TOA to reach point A. If the wave pulse of wavelength λ0 is produced at point A (Pulse 2) without disturbing the position of M it takes time TAO to reach point O. Which of the following options is/are correct?

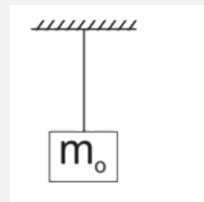
View SolutionThe block of mass m0=μL is attached to a uniform string of mass M=μL and length L as shown in the figure. If a wave pulse is produced near the block, then the time it taken to reach the ceiling is
View SolutionA block of mass M is attached with a string of mass m and length l as shown in figure. The whole system is placed on a planet whose mass and radius is three times the mass and radius of earth. Find the ratio of maximum and minimum velocity of wave pulse. Assume the acceleration due to gravity on the earth to be g.
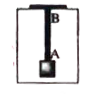
View SolutionA uniform cubical block of mass M is attached to a pulley. One end of a string, passing over the pulley is fixed to a light pole while is fixed on the bigger block and its another end is attached to a block of mass m as shown in figure. The maximum value of the mass m so that the block does not topple is : (string and pulley are ideal)

View SolutionConsider a vertical uniform string having mass per unit length lambda. A pulse is generated at the bottom. Acceleration of the pulse depends on x as
_PHY_E06_326_Q01.png)
View SolutionA mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to the rod.

View SolutionA mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to tke rod.

View Solution
