Two thin rods of same length l but of different uniform mass per unit length μ1 and μ2 respectively are joined together. The system is rotated on smooth horizontal plane as shown in figure. The tension at the joint will be 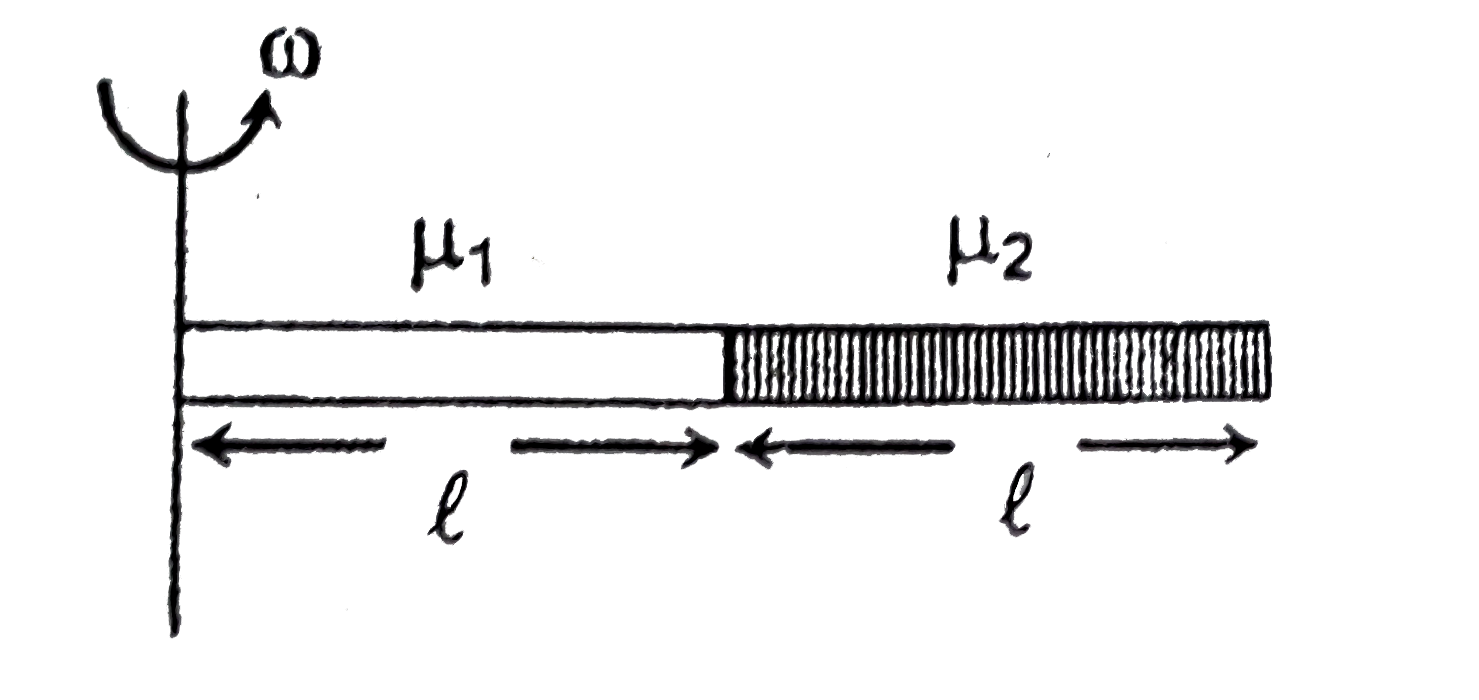
A. 32μ2l2ω2
B. 32(μ1+μ2)l2ω2
C. 32μ1l2ω2
D. 12μ1l2ω2
The correct Answer is:A
The tension at joint is due to force exerted by the root of linear density μ2.
So F=∫2llμ2dxω2x=3μ2ω2l22
Topper's Solved these Questions
Similar Questions
A rope of length 5 m has uniform mass per unit length. λ=2kgm The rope is pulled by a constant force of 10N on the smooth horizontal surface as shown in figure The tension in the rope at x = 2 m from polit A is
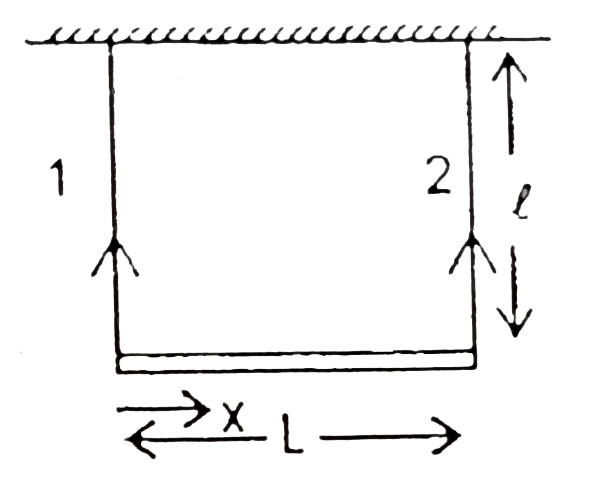
View SolutionTwo strings of the same length but different mass per unit length are used to suspend a rod whose density varies as ρ=ρ0[1+αx] as shown in the figure. The frequency of standing waves produced in the string is in the ratio n:1, when both the strings are vibrating in their fundamental mode. If the mass per unit length of string (l) is μ0, calculate the mass per unit length of the other string.
View SolutionA rod of length 2l is bent as shown in figure. Coordinates of centre of mass are
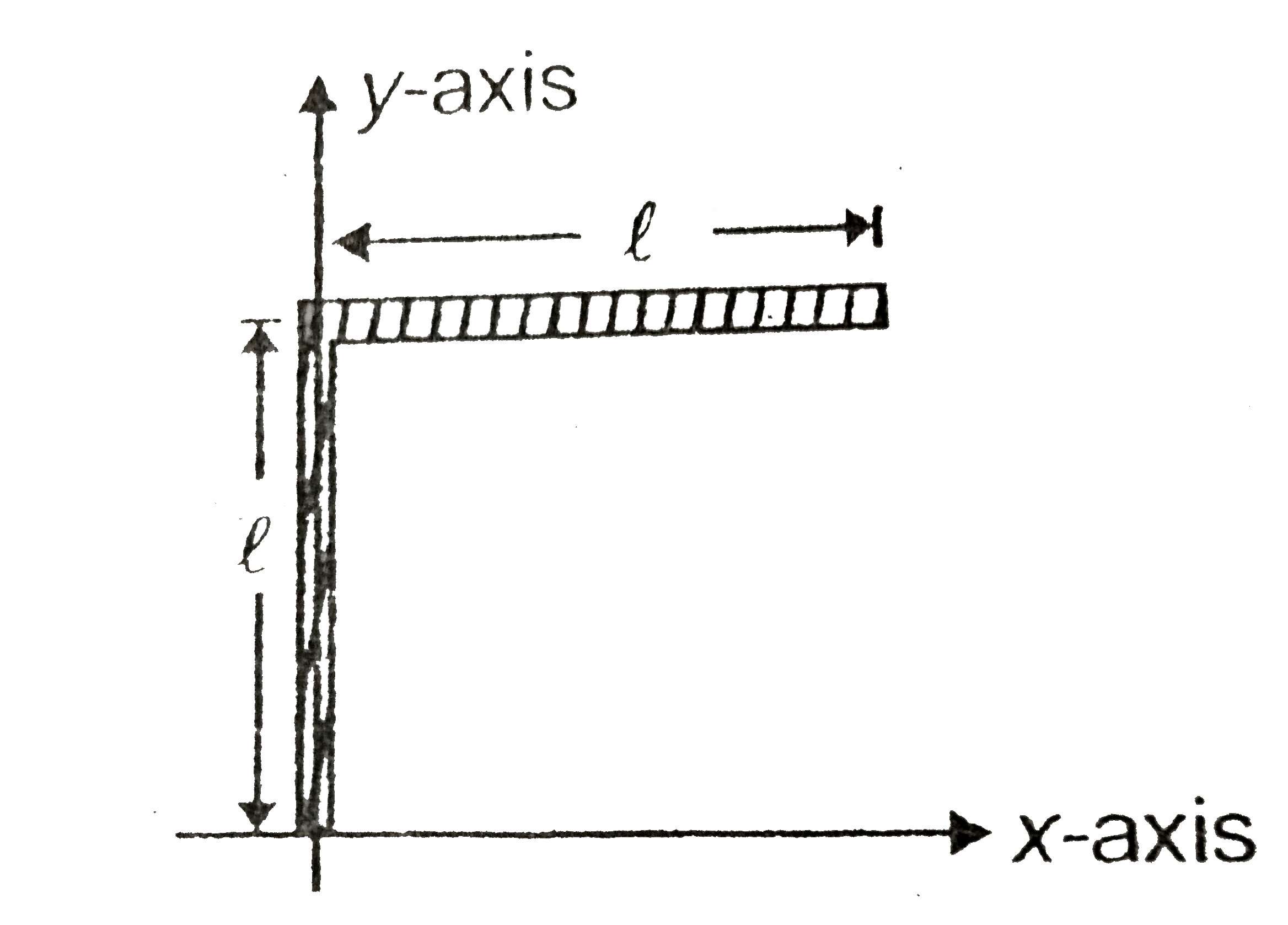
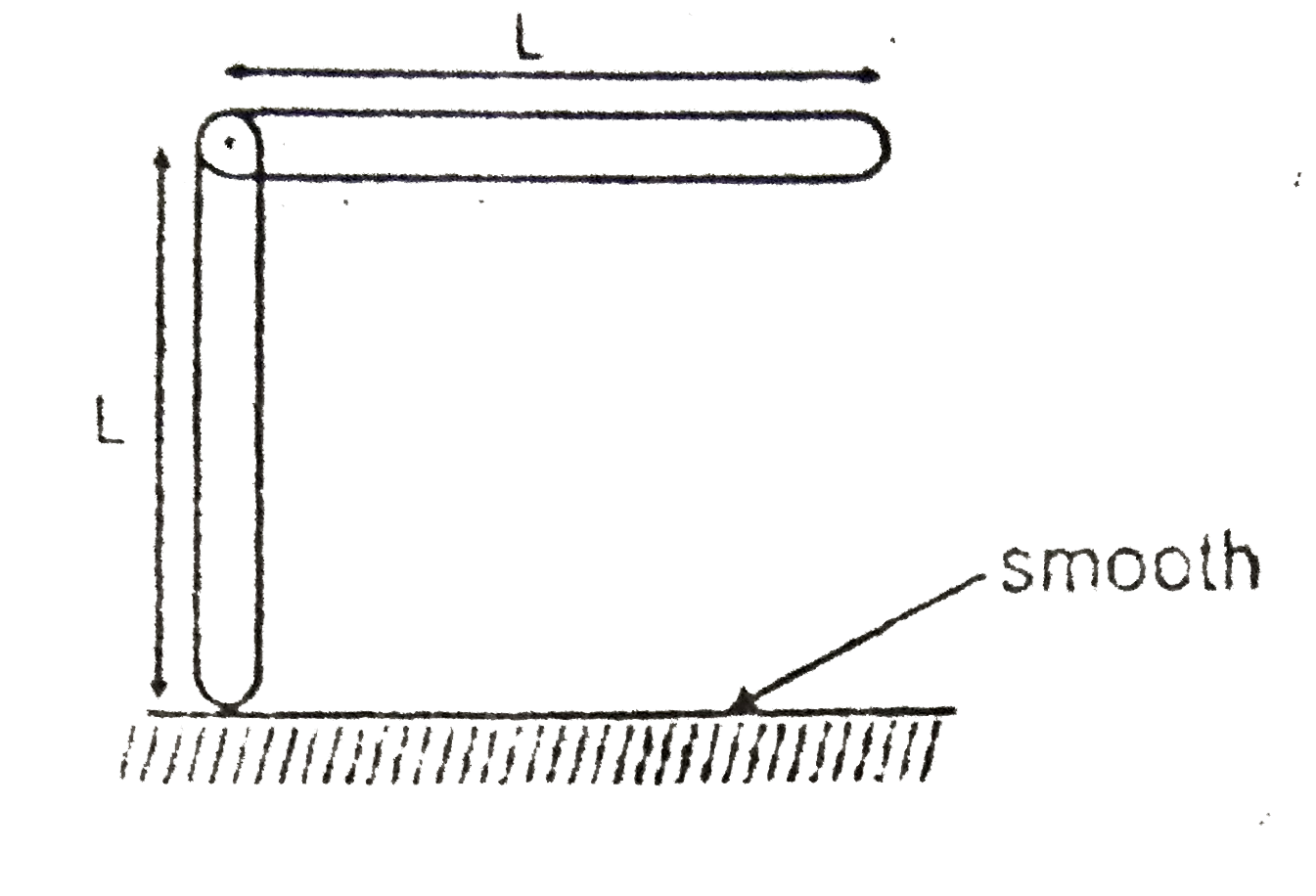
View SolutionTwo identical rods are joined at one of their ends by a pin. Joint is smooth and rods are free to rotate about the joint. Rods are released in vertical plane on a smooth surface as shown in the figure. The displacement of the joint from its initial position to the final position is (i.e. when the rods lie straight on the groun )
View SolutionA uniform rod of mass m and length L is suspended with two massless strings as shown in the figure. If the rod is at rest in a horizontal position the ratio of tension in the two strings T1T2 is:
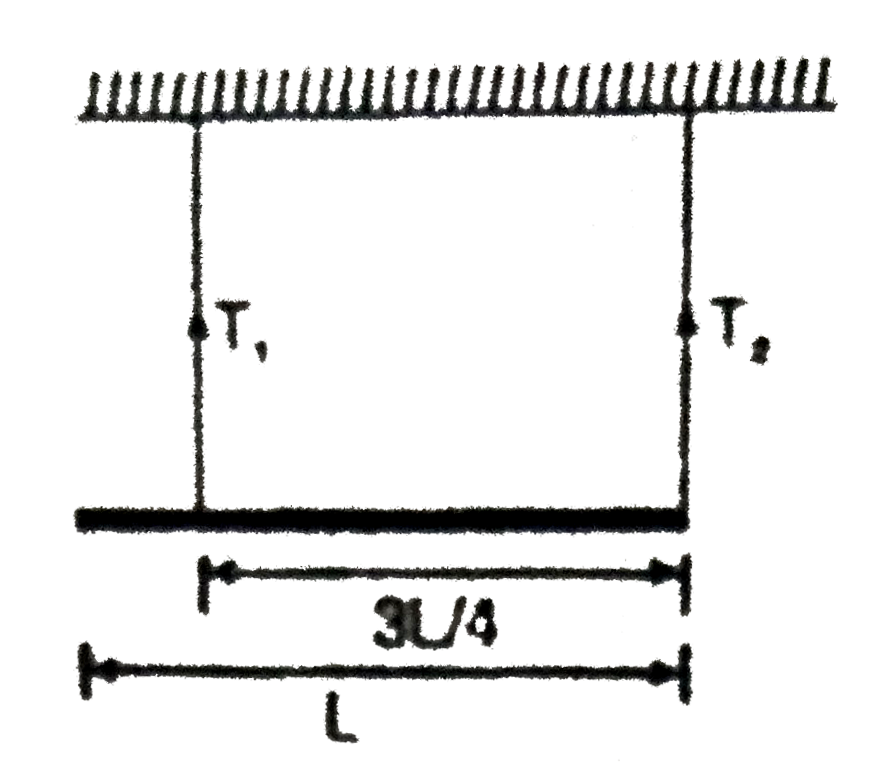
View SolutionA uniform rod of length l and mass m is hung from, strings of equal length from a ceiling as shown in figure. Determine the tensions in the strings?

View SolutionA musical instrument is made using four different metal strings, 1, 2, 3 and 4 with mass per unit length
μ,2μ,3μand4μ respectively. The instrument is played by vibrating the strings by varying the free length in between the range
L0and2L0. It is found that in string-1
(μ) at free length L0 and tension T0 the fundamental mode frequency is f0 .
List-I gives the above four strings while list-II lists the magnitude of some quantity.
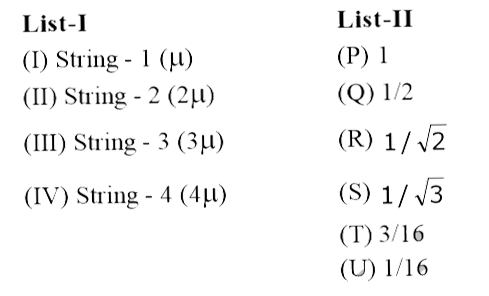
If the tension in each string is T0, the correct match for the highest fundamental frequency in f0 units will be -
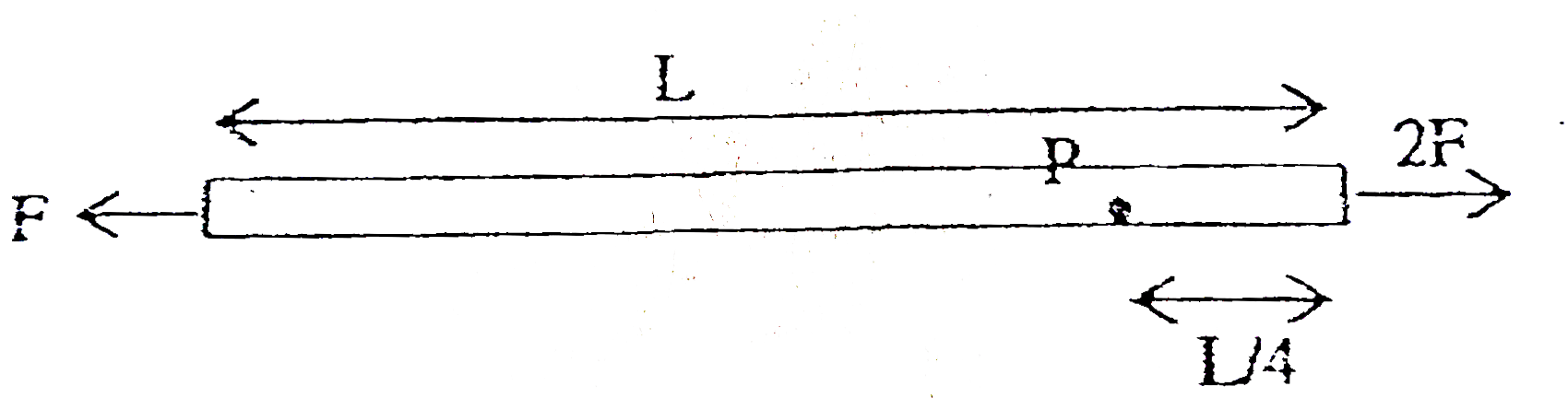
View SolutionA uniform rod of mass M and length L lies flat on a frictionless horizantal surface. Two forces F and 2F are applied along the length of the rod as shown. The tension in the rod at point P is
View SolutionA uniform rod of mass M and length L falls when it is made to stand on a smooth horizontal floor. The trajectories of the points P,Q and R as shown in the figure given below is best represented by :
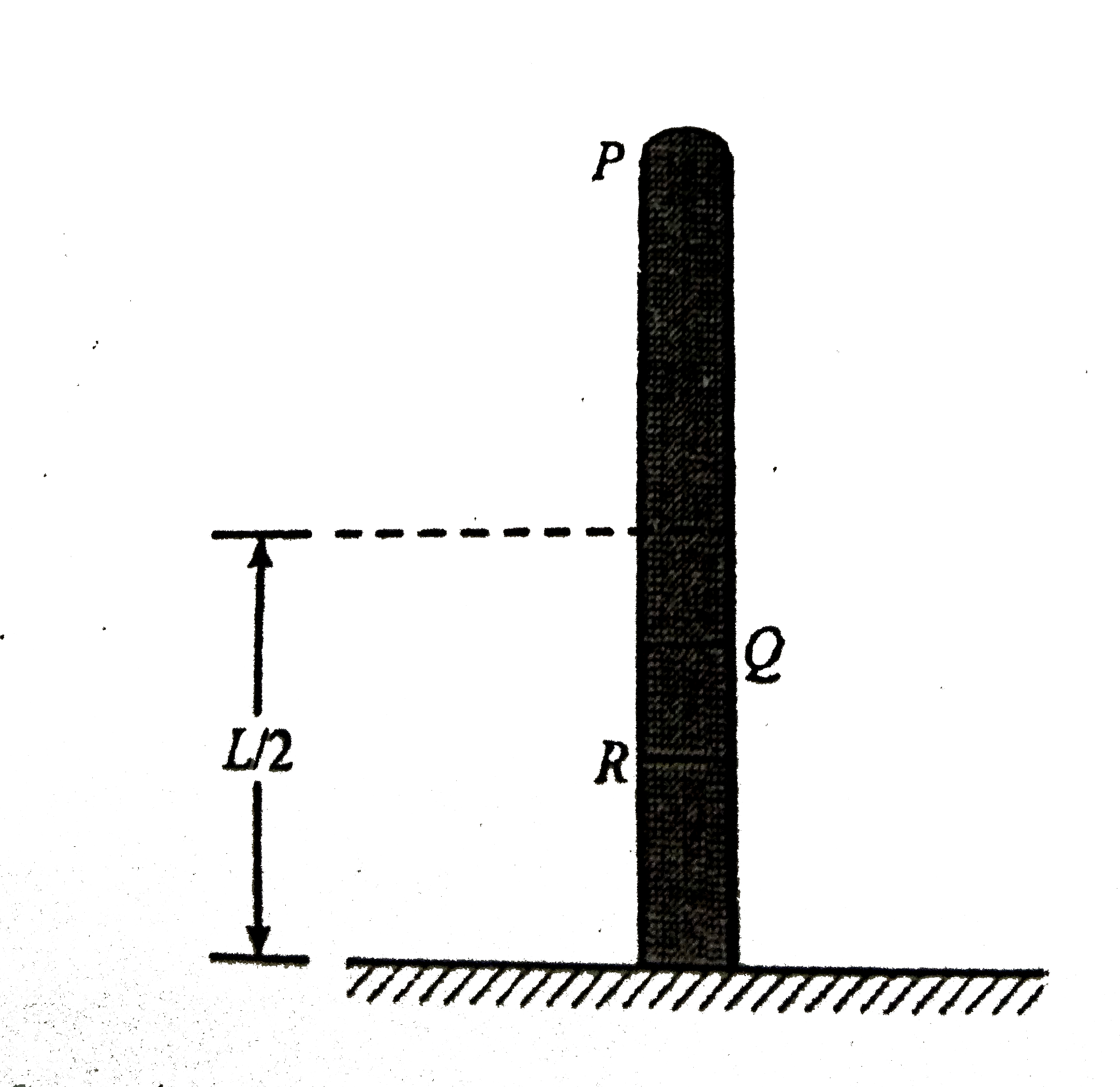
View Solution
One-fourth length of a uniform rod of mass m and length l is placed on a rough horizontal surface and it is held stationary in horizontal position by means of a light thread as shown in the figure. The thread is then burnt and the rod start rotating about the edge. Find the angle between the rod and the horizontal when it is about to slide on the edge. The coefficient of friction between the rod and surface is μ.
View Solution
