Consider a long solenoid of radius R which has n turns per unit length. A time dependent current I=I0sinωt flows solenoid, magnitude of electric field at a perpendicular distance r<R, from the axis of symmetry of solenoid is found to be E=α4ωμ0nI0rcosωt, where α is pure number and μ0 is permability of free space. Find α
To find the value of α in the given expression for the electric field E around a long solenoid, we can follow these steps:
Step 1: Understanding the Problem
We have a long solenoid with radius R and n turns per unit length. A time-dependent current I=I0sin(ωt) flows through the solenoid. We need to find the value of α in the expression for the electric field at a distance r<R from the axis of the solenoid.
Step 2: Magnetic Field Inside the Solenoid
The magnetic field B inside a long solenoid is given by:
B=μ0nI
where μ0 is the permeability of free space.
Step 3: Magnetic Flux Calculation
The magnetic flux Φ through a circular area of radius r inside the solenoid is given by:
Φ=B⋅A=B⋅πr2
Substituting for B:
Φ=μ0nI⋅πr2
Step 4: Time Derivative of Magnetic Flux
To find the induced electric field, we need to compute the time derivative of the magnetic flux:
dΦdt=ddt(μ0nI⋅πr2)
Since I=I0sin(ωt), we differentiate:
dΦdt=μ0nπr2dIdt=μ0nπr2I0ωcos(ωt)
Step 5: Applying Faraday's Law of Induction
According to Faraday's law, the induced electric field E around the solenoid is given by:
∮E⋅dl=−dΦdt
For a circular path of radius r, the line integral becomes:
E⋅2πr=−dΦdt
Substituting the expression for dΦdt:
E⋅2πr=−μ0nπr2I0ωcos(ωt)
Step 6: Solving for the Electric Field E
Rearranging the equation gives:
E=−μ0nI0ωrcos(ωt)2
Taking the magnitude (ignoring the negative sign):
E=μ0nI0ωrcos(ωt)2
Step 7: Comparing with the Given Expression
We are given that:
E=α4ωμ0nI0rcos(ωt)
Setting the two expressions for E equal to each other:
μ0nI0ωrcos(ωt)2=α4ωμ0nI0rcos(ωt)
Step 8: Solving for α
By comparing coefficients, we can cancel nI0rcos(ωt) from both sides (assuming they are non-zero):
μ0ω2=α4ωμ0
Cross-multiplying gives:
α=2μ20ω2
Final Answer
Thus, the value of α is:
α=2
We have a long solenoid with radius R and n turns per unit length. A time-dependent current I=I0sin(ωt) flows through the solenoid. We need to find the value of α in the expression for the electric field at a distance r<R from the axis of the solenoid.
The magnetic field B inside a long solenoid is given by:
B=μ0nI
where μ0 is the permeability of free space.
The magnetic flux Φ through a circular area of radius r inside the solenoid is given by:
Φ=B⋅A=B⋅πr2
Substituting for B:
Φ=μ0nI⋅πr2
To find the induced electric field, we need to compute the time derivative of the magnetic flux:
dΦdt=ddt(μ0nI⋅πr2)
Since I=I0sin(ωt), we differentiate:
dΦdt=μ0nπr2dIdt=μ0nπr2I0ωcos(ωt)
According to Faraday's law, the induced electric field E around the solenoid is given by:
∮E⋅dl=−dΦdt
For a circular path of radius r, the line integral becomes:
E⋅2πr=−dΦdt
Substituting the expression for dΦdt:
E⋅2πr=−μ0nπr2I0ωcos(ωt)
Rearranging the equation gives:
E=−μ0nI0ωrcos(ωt)2
Taking the magnitude (ignoring the negative sign):
E=μ0nI0ωrcos(ωt)2
We are given that:
E=α4ωμ0nI0rcos(ωt)
Setting the two expressions for E equal to each other:
μ0nI0ωrcos(ωt)2=α4ωμ0nI0rcos(ωt)
By comparing coefficients, we can cancel nI0rcos(ωt) from both sides (assuming they are non-zero):
μ0ω2=α4ωμ0
Cross-multiplying gives:
α=2μ20ω2
Thus, the value of α is:
α=2
Topper's Solved these Questions
Similar Questions
A long solenoid has a radius a and number of turns per unit length is n. If it carries a current i, then the magnetic field on its axis is directly proportional to
View SolutionA conducting ring of radius b is placed coaxially in a long solenoid of radius a (b < a) having n turns per unit length. A current i=i0, cosωt flows through the solenoid. The induced emf in the ring is
View Solution
Knowledge Check
A solenoid of length 0.6 m has a radius of 2 cm and is made up of 600 turns If it carries a current of 4 A, then the magnitude of the magnetic field inside the solenoid is
A6.024×10−3TB8.024×10−3TC5.024×10−3TD7.024×10−3T
The current in a long solenoid of radius R and having n turns per unit length is given by i=i0sinωt. A coil having N turns is wound around it near the centre. Find (a) the induced emf in the coil and (b) the mutual inductance between the solenoid and the coil.
View SolutionA tightly wound solenoid of radius 'a' and length 'l' has n turns per unit length. It carries an electric current i. Magnetic field at a distance l4 from one of the end (inside the solenoid on its axis) is B=μ0ni(√5+3)√K for l=4a. Then find the value of K.
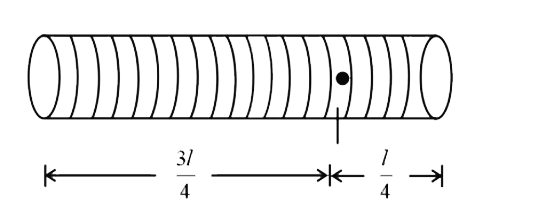
View SolutionA tightly wound solenoid of radius 'a' and length 'l' has n turns per unit length. It carries an electric current i. Magnetic field at a distance l4 from one of the end (inside the solenoid on its axis) is B=μ0ni(√5+3)√K for l=4a. Then find the value of K.

View SolutionA long solenoid of radius R carries a time (t) – dependent current I=I0(t−2t2) A circular ring of radius = R is placed near the centre of the solenoid and plane of ring makes an angle 30∘ with the axis of solenoid. The time at which magnetic flux through the ring is maximum is :
View SolutionA long solenoid of radius R carries a time (t) – dependent current I=I0(t−2t2) A circular ring of radius = R is placed near the centre of the solenoid and plane of ring makes an angle 30∘ with the axis of solenoid. The time at which magnetic flux through the ring is maximum is :
View SolutionA long thin solenoid has 900tuns/metre and radius 2.50cm,. The current in the solenoid is increasing at a uniform rate of 60A/s. What is the magnitude of the induced electric field at a point?
a. 0.5cm from the axis of the solenoid.
b. 1.0cm from the axis of the solenoid.
View SolutionA long solenoid of radius R carries a time dependent current I=I0t(1–t). A ring of radius 2R is placed coaxially near its centre. During the time interval0≤t≤1, the induced current IR and the induced emf VR in the ring vary as:
View Solution
