There are two identical small holes of area of cross section a on the opposite sides of a tank containing liquid of density ρ. The differences in height between the holes is h. The tank is resting on a smooth horizontal surface. The horizontal force which will have to be applied on the tank to keep it in equilibrium is

h1/2
h
h3/2
h2
The correct Answer is:B
Step by step video & image solution for There are two identical small holes of area of cross section a on the opposite sides of a tank containing liquid of density rho. The differences in height between the holes is h. The tank is resting on a smooth horizontal surface. The horizontal force which will have to be applied on the tank to keep it in equilibrium is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FLUID MECHANICSBOOK - RESONANCE ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise- 2 PART - I
18 Videos
- FLUID MECHANICSBOOK - RESONANCE ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise- 2 PART - II
6 Videos
- FLUID MECHANICSBOOK - RESONANCE ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise- 1 PART - II Section (B)
7 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise
52 Videos
- FULL TEST 1BOOK - RESONANCE ENGLISHCHAPTER - FULL TEST 1EXERCISE - Exercise
30 Videos
Similar Questions
There are two identical small holes of area of cross section a on the opposite sides of a tank containing liquid of density ρ. The differences in height between the holes is h. The tank is resting ona smooth horizontal surface. The horizontal force which will have to be applied on the tank to keep it inequilibrium is

View SolutionThere are two identical small holes on the opposite sides of a tank containing a liquid. The tank is open at the top. The difference in height between the two holes is h. As the liquid comes out of the two holes. The tank will experience a net horizontal force proportional to.
 .
.
View Solution
Knowledge Check
A liquid of density ρ flows along a horizontal pipe of uniform cross-section A with a velocity v through a right angled bend as shown in fig. What force has to be exerted at the bend to hold the pipe in equilibrium ? .
A2aρv2Baρv2/√2C√2aρv2Daρv2
A solid sphere of radius R is resting on a smooth horizontal surface. A constant force F is applied at a height h from the bottom. Choose the correct alternative.

View Solution
A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B is
View SolutionA sealed tank containing a liquid of density ρ moves with horizontal acceleration a as shown in the figure. The difference in pressure between two points A and B will be

View SolutionOn the opposite sides of vertical vessel filled with water, two identical holes are opened. If area of cross-section for each is a and difference of height of these two is h and p is density of water, then force on the vessel is
View SolutionThere are two holes one each along the opposite sides of a wide rectangular tank. The cross section of each hole is 0.01m2 and the vertical distance between the holes is one meter. The tank is filled with water. The net force on the tank in newton when water flows out of the holes is (density of water 1000kg/m3)
View SolutionA cylindrical tank having cross - sectional area A=0.5m2 is filled with two liquids of density ρ1=900 kg m−3andρ2=600 kg m−3 , to a height a =6cm2 is made in right vertical wall at a height y = 20 cm from the bottom . A horizontal force F is applied on the tank to keep it in static equilibrium . The tank is lying on a horizontal surfaces . Neglect mass of cylindrical tank camparison to mass of liquids ( take g=10ms−2)
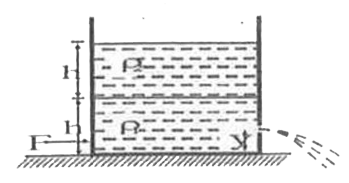
Minimum and maximum values of F to keep the cylinder in static just after the water starts to spill through the hole . If the co - efficient of static friction between contact surfaces is 0.01
View SolutionA small illuminated bulb is at the bottom of a tank, containing a liquid of refractive index μ upto a height H. Find the expression for the diameter of an opaque disc, floating symmetrically on the liquid surface in order to cut- off the light from the bulb.
View Solution
